Глава vjj

СИЛЫ ИНЕРЦИИ, РАЗВИВАЮЩИЕСЯ В МЕХАНИЗМАХ МАШИН ВО ВРЕМЯ ХОДА, И ВОЗДЕЙСТВИЕ МАШИНЫ НА

РАМУ И ФУНДАМЕНТ

1. Силы инерции кривошипного механизма одноцилиндрового

поршневого двигателя

Аналитическое исследование движения кривошипного меха­низма. Вопрос об учете сил инерции в кривошипном механизме обычно решается аналитическим путем, так как для этого типа механизмов аналитические выражения для ускорений звеньев,

необходимые в подсчетах сил инерции, при встречающихся соотношениях между длинами звеньев, получаются достаточно простыми. Нам прежде всего по­надобятся аналитические выра-Фиг. 75 жения для ускорения 3-го звена

(ползуна, штока и поршня) и для ускорения центра тяжести шатуна. Обратимся к их выводу. Составим выражение для расстояния ползуна от главного вала О, пользуясь схемой механизма (фиг. 75) и введя в качестве основ­ного параметра угол поворота кривошипа ?. Из чертежа имеем

хь = OA' + A'B = r cos ф-Н cos & (126)

Так как АА\ с одной стороны, равно

A4' = rsin<?,

а, с другой стороны,

ЛЛ' =/sin

то

rsin<p = /sin р,

или

Ho для выражения (126) нам нужен cosf), поэтому

cosjBeBJ/l—sin*[*«= 1 1 — ^ siir 9, (127>

Так как величина X кривошипных механизмов небольшая:

в среднем v -5 . -*« ' .... то значение корня может быть взято приближенно, воспользовавшись разложением корня по строке Ньютона н ограничиваясь в разложении ряда третьими степе-нами X (с точностью до Xе). Произведя это разложение, полу­чим

cos р =^ (1— X» sins ф)''* — I—Vt *e sin1 ф —

— Sin4 Ф — «ГГл * s1h1'Ф — J. %

Ограничиваясь членами с точностью до х?, будем иметь

cos р Si 1— /tj^ sin5 ф = 1---4- cos* ф%

Поэтому с этой точностью получим

xh = г cos*© + м 1--— ~4—— cos 2ф I.

\ 4 4 * /

Для разыскания скорости поршня диференцируем это выра­жение но времени, придерживаясь порядка

хж _dxe_ dxp _ <1хъ

v*~ dt — df \ dt" d? 0)1'

найдем

\\ = —гсо/ sin© + тгsin2©V (128)

Знак минус указывает, что, при положительном значении вы­ражения в скобках, направление скорости будет обратным на­правлению возрастающих л\ т. е. по направлению к главному валу.

Для разыскания ускорения \\"ь диференцируем уравнение (128) по времени, предполагая угловую скорость вращения постоянной, т. е. по схеме

117 rf? _ dV6

wb — dt df dt dt ,#

найдем

Wb = — r»? (cos ф -f /. cos 2ф> (129)

Звак минус указывает, что ускорение будет направлено против возрастающих х, т. е. к главному валу при значении выражения

в скобках >0.

Как ускорение так и скорость Vt по ф-лам (128) и (129> получаются с точностью до членов с

39

Более точные значения cos з, х#, к, и Wb, разложенные по косинусам кратных дуг, будут

cos £г= (1— V. >>" - Ve. — 'Ли —. •.) + + 0/« X2 + Vieх< 4- 15Аи х6 + • • •) cos 6а>; = л cos <р + / [(1 — V4 X» — 3; 64 X" — */1И х° +...) -4-+ О/. ^ + Vie ^' +1V»» х6 + • • •) cos 2? — - 07м v + %т х° + ■ ■ •) cos 4с? + (Тем х° + • • •) cos б

V, = — г со, [sin ? + ('/2 X + у, X' + "/ив X5 +...) sin 2f-

- (Vie ^ + Ve.Х5 + • • •) sin 4 ? + (»/„. Xs +...) sin 6?];

jf* = — ''<"? [cos с? +.(Х +1/.хз + 15/i2s >5 +...) cos 2?-— ОД хз + Ve X» +...) cos 4 с? + (»/lt8 X5 +...) cos 4<р].

Или при

52 = ^+1/^3+16/i,b^ + ...

°е 128 5

(130) (131)

(132)

= — г ад2 (cos <р + Б2 cos 2? 4-£4 cos 4<р-f- Б6 cos 6<р). (131а)

Численные значения коэфициентов В2> Б4, BQ:

К 1/3.5 1/4 1/4,5 1/5 1/6 1/7

в2 0,2918 0,2540 0,2250 0,2020 0,1678 0,1436

в\ —0,0062 -0,0041 —0,0028 —0,0020 —0,0012 —0.0007

вб 0,000126 0,000069 0,000038 0,000022 0,000009 0,000004

Составим еще выражение для ускорения W —центра тяжести шатуна.

Из теоремы подобия для группы точек, жестко между собою связанных, как Л, 5, С, известно из кинематики, что на плане уско­рений конец вектора а) бJ ускорения \VC дол-

а i w жен находиться на

Wqs^ _____в (Х<^ отрезке, проведен-

ном (фиг. 76, б) ме­жду концами векто-Фиг. 76. ров Wa и Wb> и де-

лить этот отрезок в

отношении АС: СВ. То же самое получается и при построении ускорений в самих точках Л, В, С шатуна (фиг. 76, а). Применяя эту теорему подобия для проекций ускорения на оси х и у, по­лучим: 1) вектор Wex будет оканчиваться на прямой, соединяю­щей концы векторов wax и Wb (фиг. 77, а), откуда

Wer « Wb ^ + Wrs if ; (133)

40

2) вектор U' .v, будет оканчиваться на прямой, соединяющей ieu вектопа \\

л м i

% 07

(134)

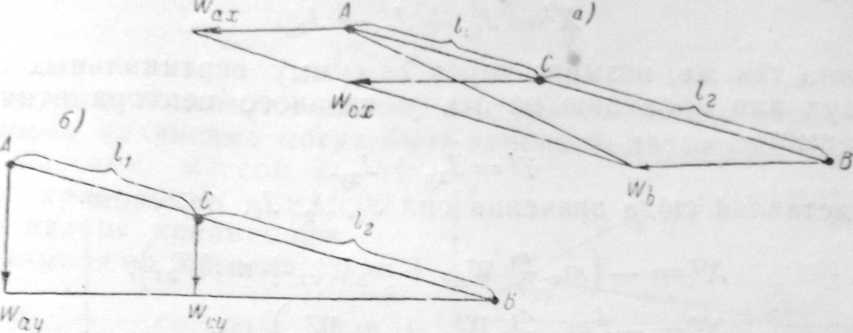
Фиг

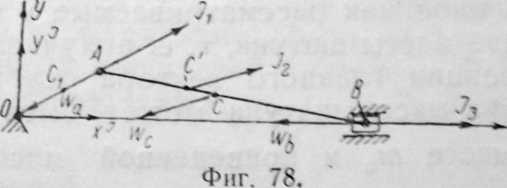
Выражение для суммарной горизонтальной и суммарной вертикальной сил инерции кривошипного механизма. В даль­нейшем нам понадобится выражение для суммарной составля­ющей сил инерции как в горизонтальном, так и в вертикальном направлении; обратимся к их выводу. На фиг. 78 изображены силы инерции, возникающие в частях кривошипного механизма при равномерном вращении кривошипа:

Vj — центробежная сила кривошипа,

Л — сила инерции шатуна,

J,— сила инерции поступательно движущихся масс поршня,

штока и крейцкопфа. Обозначим через ех — эксцентриситет положения центра

тяжести Тогда на гл. V.

i кривошипа, основании § 1,

Л = mKet ш2,

где шк — масса кривошипа.

Так как г ш| == Wn— уско­рение пальца кривошипа (предполагая вращение кривошипа равномерным), то

У, т

в»

здесь масса тк — носит название массы кривошипа» отнесенной

к его пальцу Л.

Выражение для Л по § 3 той же гл. V будет

где /я, — масса шатуна, a Wc—ускорение центра тяжести ша­туна.

40