
- •Задачи линейного программирования
- •Постановка задачи
- •Задачи для решения
- •1.2. Свойства решений задач линейного программирования
- •Графический метод решения задач линейного программирования Случай двух переменных
- •Случай многих переменных
- •1.4.2.Симплексный метод
- •Этап 1. Определение начального опорного плана.
- •Случай вырождения
- •Задачи для решения
- •Метод искусственного базиса
- •Задачи для решения
- •1.5. Теория двойственности в линейном программировании
- •1.5.1. Постановка задачи
- •Некоторые частные случаи
- •1.5.2. Основные теоремы двойственности
- •Задачи для решения
- •1.5.3. Геометрическая интерпретация двойственных задач
- •1.5.4. Двойственный симплекс – метод
- •Этап 1. Определение начального опорного плана (псевдоплана).
- •Этап 2. Определение оптимального плана.
- •Задачи для решения
- •1.6. Экономическая интерпретация двойственности
- •1.6.1. Анализ моделей на чувствительность.
- •Использование графического метода.
- •Использование симплекс-метода.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Применение компьютера Инструкция по использованию надстройки «Поиск решения»
- •1.10. Решение задачи с использованием
Случай вырождения
Опорное решение, в котором хотя бы одна из базисных переменных принимает нулевое значение, называется вырожденным решением. Задача линейного программирования, имеющая хотя бы одно вырожденное решение, - вырожденной задачей.
Существование вырожденного решения может привести к зацикливанию процесса вычислений. То есть, после нескольких шагов вычислений можно вернуться к ранее встречавшемуся набору базисных и свободных переменных. Особенно опасно «зацикливание» при автоматизированных вычислениях.
Устранение
«зацикливания» возможно с помощью
следующего правила. Если на каком-то
этапе вычислений при выборе разрешающей
строки возникает неопределённость, то
есть оказывается несколько равных
минимальных отношений
![]() ,
то следует выбрать ту строку, для которой
будет наименьшим отношение элементов
следующего столбца к разрешающему. Если
при этом снова окажутся равными
минимальные отношения, необходимо
перейти к рассмотрению следующего
столбца, и так до тех пор, пока разрешающая
строка не определится однозначно.
,
то следует выбрать ту строку, для которой
будет наименьшим отношение элементов
следующего столбца к разрешающему. Если
при этом снова окажутся равными
минимальные отношения, необходимо
перейти к рассмотрению следующего
столбца, и так до тех пор, пока разрешающая
строка не определится однозначно.
Пример.6. Найти какой-либо опорный план задачи
![]() ,
,
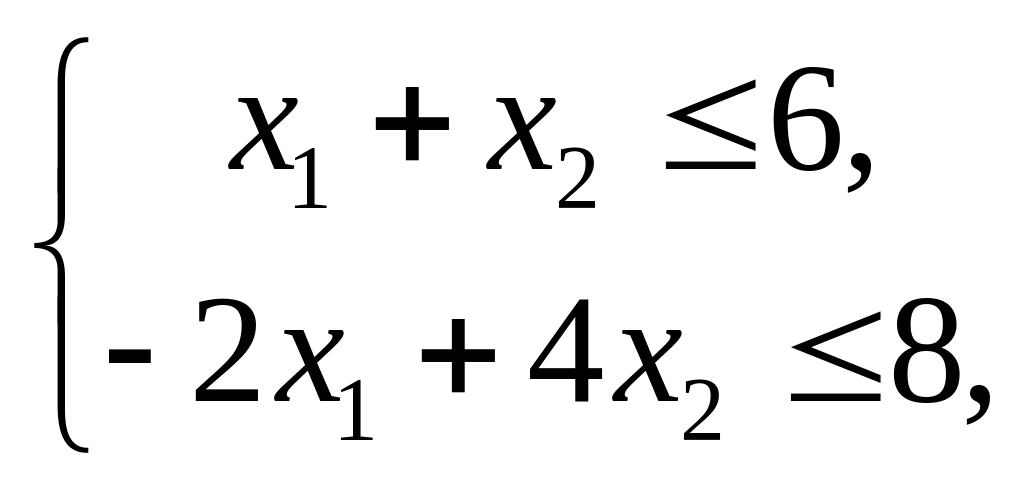
Решение. Введём
в систему ограничений неотрицательные
балансовые переменные
![]() и
и
![]() .
.
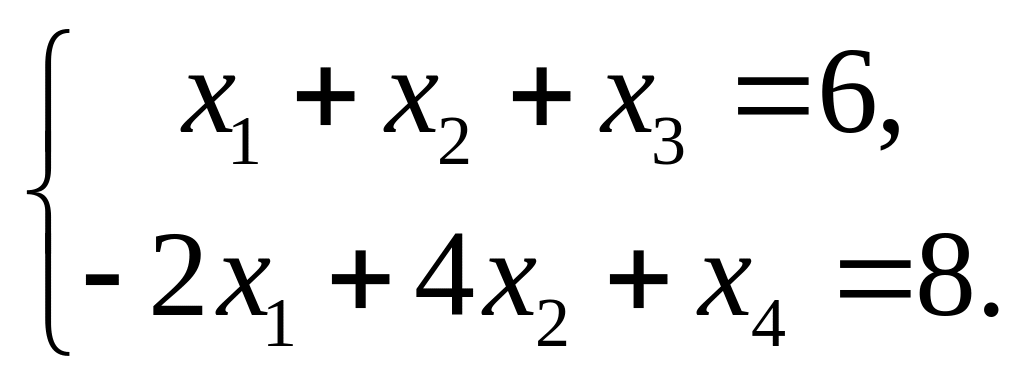
Балансовые переменные сделаем базисными
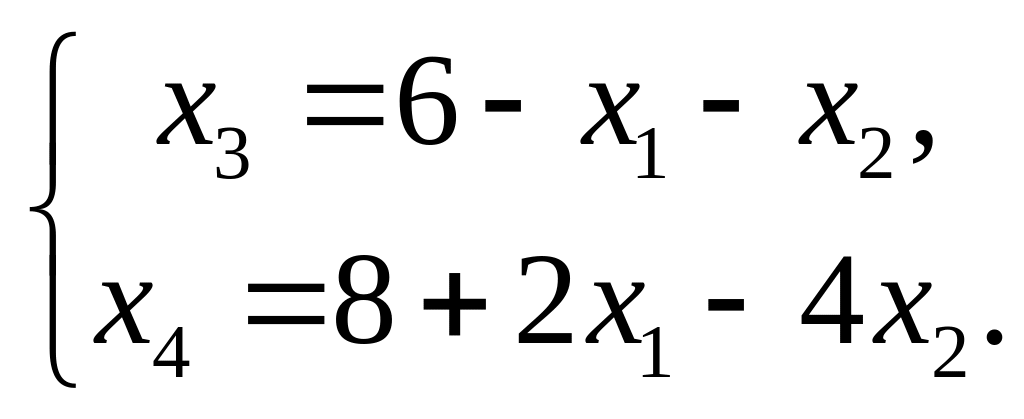
Составим симплексную таблицу (табл.1.6)
Таблица 1.6 Таблица 1.7
Б.П. |
1 |
С.П. |
С.С. |
|
Б.П |
1 |
С.П. |
||
|
|
|
|
|
|
||||
= |
6 |
1 |
1 |
6/1=6 |
|
= |
4 |
3/2 |
-1/4 |
= |
8 |
-2 |
|
8/4=2 |
|
= |
2 |
-1/2 |
1/4 |
F = |
0 |
-4 |
-6 |
|
|
F = |
12 |
-7 |
3/2 |
Из таблицы видно,
что начальный опорный план есть, так
как в столбце свободных членов все
элементы положительны -
![]() .
Можно найти другой опорный план. Для
этого в F
– строке выбираем элемент (-6),
соответствующий переменной
.
Столбец под переменной
будет разрешающим. Затем находим
минимальное отношение элементов столбца
свободных членов к элементам разрешающего
столбца. Поместим эти отношения в столбец
(С.С.). Минимальное значение находится
в строке, где находится элемент
.
Эта строка будет разрешающей. Разрешающий
элемент стоит на пересечении этой строки
и столбца, он равен 4.
.
Можно найти другой опорный план. Для
этого в F
– строке выбираем элемент (-6),
соответствующий переменной
.
Столбец под переменной
будет разрешающим. Затем находим
минимальное отношение элементов столбца
свободных членов к элементам разрешающего
столбца. Поместим эти отношения в столбец
(С.С.). Минимальное значение находится
в строке, где находится элемент
.
Эта строка будет разрешающей. Разрешающий
элемент стоит на пересечении этой строки
и столбца, он равен 4.
В таблице 1.7:
- строка, в которой находится , получена делением разрешающей строки таблицы 1.6 на разрешающий элемент 4;
- столбец, в котором находится , получен делением разрешающего столбца таблицы 1.6 на разрешающий элемент 4 и переменой знака на противоположный;
Остальные элементы
вычислены по правилу прямоугольников,
в том числе и элементы F
– строки.
Например, для вычисления элемента
![]() строим прямоугольник, показанный в
таблице 1.6, и вычисляем этот элемент по
формуле прямоугольников (1.10)
строим прямоугольник, показанный в
таблице 1.6, и вычисляем этот элемент по
формуле прямоугольников (1.10)
![]() .
Аналогично вычислены остальные элементы
таблицы 1.7. В новой таблице меняем местами
переменные
и
.
Аналогично вычислены остальные элементы
таблицы 1.7. В новой таблице меняем местами
переменные
и
![]() .
.
В итоге, после
одного шага симплексных преобразований,
получен ещё один опорный план исходной
задачи
![]() .
Он так же, как и предшествующий не
является оптимальным, так как в F
– строке
есть отрицательный элемент.
.
Он так же, как и предшествующий не
является оптимальным, так как в F
– строке
есть отрицательный элемент.
Пример 7. Для предшествующей задачи найти оптимальный опорный план.
Решение. В таблице 1.7 уже определён один из опорных планов, который можно считать начальным. Чтобы получить оптимальный план, выберем в качестве разрешающего столбца тот, в котором находится коэффициент (-7) F – строки. Добавим к таблице 1.7 симплексный столбец, полученный делением свободных членов на элементы разрешающего столбца
Таблица 1.8 Таблица 1.9
Б.П. |
1 |
С.П. |
С.С. |
|
Б.П. |
1 |
С.П. |
||
|
|
|
|
||||||
= |
4 |
|
-1/4 |
8/3 |
|
= |
8/3 |
|
|
= |
2 |
-1/2 |
¼ |
- |
|
= |
10/3 |
|
|
F = |
12 |
-7 |
3/2 |
|
|
F = |
92/3 |
14/3 |
1/3 |
В симплексном
столбце таблицы 1.8 только один элемент,
он и определяет разрешающую строку.
Значит, разрешающим элементом будет
элемент 3/2, расположенный на пересечении
столбца, в котором находится
,
и строки, в которой находится
.
В таблице 1.9 меняем местами
и
.
Вычислим только столбец свободных
членов и элементы F
– строки.
Если в них все элементы будут положительными,
то оптимальное решение достигнуто. В
таблице 4 именно так и есть. В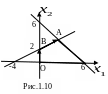 се
элементы в столбце свободных членов и
в F
– строке
положительны, значит достигнут оптимальный
план. При этом
се
элементы в столбце свободных членов и
в F
– строке
положительны, значит достигнут оптимальный
план. При этом
![]() ,
а оптимальный план
,
а оптимальный план
![]() .
Решение можно интерпретировать
геометрически. На Рис.1.10. точка О(0;0)
является опорным планом
,
точка В(0;2) – опорным планом
.
Решение можно интерпретировать
геометрически. На Рис.1.10. точка О(0;0)
является опорным планом
,
точка В(0;2) – опорным планом
![]() ,
точка А(8/3;10/3) - оптимальным опорным
планом
,
точка А(8/3;10/3) - оптимальным опорным
планом
![]() .
Ломаная ОВА (рис. 1.10) показывает путь,
продвигаясь по которому от одного
опорного плана к другому, достигнуто
оптимальное решение.
.
Ломаная ОВА (рис. 1.10) показывает путь,
продвигаясь по которому от одного
опорного плана к другому, достигнуто
оптимальное решение.
Пример 8. Найти оптимальный опорный план задачи
![]() ,
,
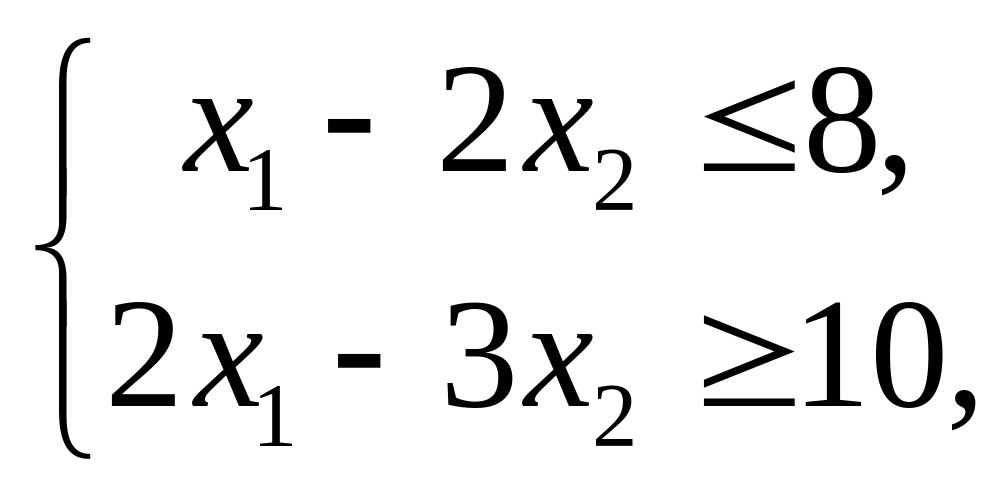
Решение. Приведём систему ограничений к каноническому виду, введя неотрицательные балансовые переменные и .
![]()
Откуда
![]()
Составим симплексную таблицу (табл.1.10).
Таблица 1.10 Таблица 1.11
Б.П. |
1 |
С.П. |
|
Б.П |
1 |
С.П. |
||
|
|
|
|
|
||||
= |
8 |
1 |
-2 |
|
|
8 |
-1/2 |
-1/2 |
= |
-10 |
|
3 |
|
|
5 |
-1/2 |
-3/2 |
F = |
0 |
-6 |
-5 |
|
F = |
30 |
3 |
-14 |
В столбце свободных
членов есть отрицательный элемент,
следовательно, данный план
![]() не является опорным.
не является опорным.
В строке, в которой находится неизвестная , находим единственный отрицательный элемент (-2), который будет разрешающим.
Делим на этот элемент все остальные элементы разрешающей строки, и меняем местами неизвестные и . Получаем табл. 1.11.
П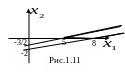 олученный
план является опорным, но не является
оптимальным, так как один из элементов
F
– строки
является отрицательным. Для отыскания
оптимального плана необходимо выбрать
в качестве разрешающего столбца тот, в
котором находится элемент (-14). Но
следует обратить внимание на то, что в
соответствующем столбце нет ни одного
положительного элемента. Это говорит
о том, что задача не имеет решения.
Геометрически это представлено на Рис.
1.11. Область решений является неограниченной.
олученный
план является опорным, но не является
оптимальным, так как один из элементов
F
– строки
является отрицательным. Для отыскания
оптимального плана необходимо выбрать
в качестве разрешающего столбца тот, в
котором находится элемент (-14). Но
следует обратить внимание на то, что в
соответствующем столбце нет ни одного
положительного элемента. Это говорит
о том, что задача не имеет решения.
Геометрически это представлено на Рис.
1.11. Область решений является неограниченной.
Пример 9. Найти оптимальное решение задачи
![]() ,
,

Решение. Перейдём
в ограничениях задачи от симметричной
формы к канонической, для чего введём
балансовые переменные
![]()
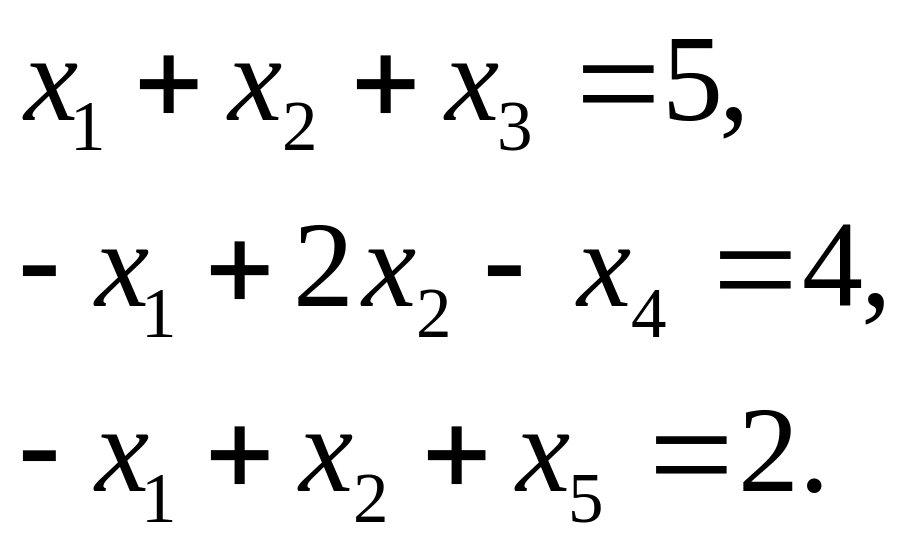
Балансовые
переменные сделаем базисными. Выразим
каждую из них через свободные переменные
![]()
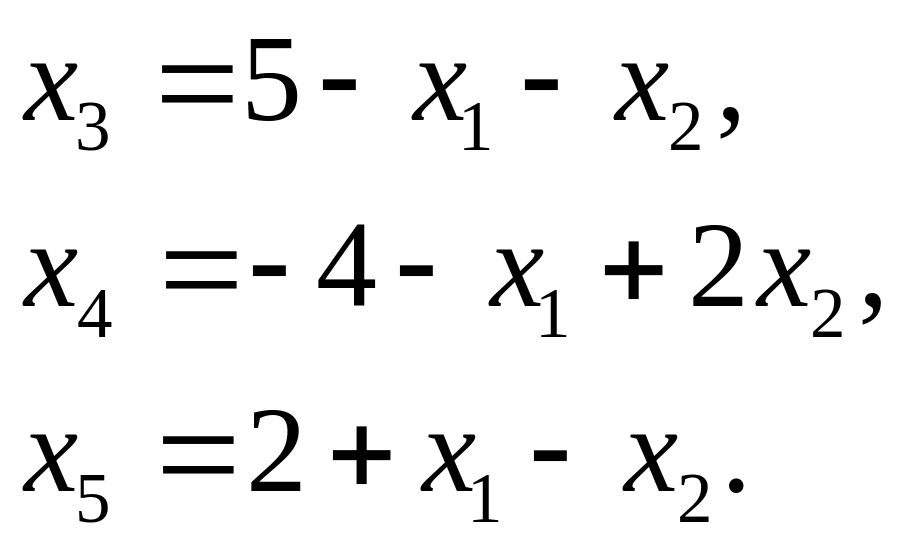
Составим симплексную таблицу 1.12.
Таблица 1.12 Таблица 1.13
Б.П. |
1 |
С.П. |
С.С. |
|
Б.П. |
1 |
С.П. |
С.С. |
||
|
|
|
|
|
||||||
|
5 |
1 |
1 |
5 |
|
|
3 |
|
½ |
2 |
|
-4 |
1 |
|
2 |
|
|
2 |
-1/2 |
-1/2 |
- |
|
2 |
-1 |
1 |
2 |
|
|
0 |
-1/2 |
½ |
- |
F= |
0 |
-2 |
-3 |
|
|
F= |
6 |
-1/2 |
-3/2 |
|
Найденный план не
является опорным, так как у него одна
координата отрицательная
![]() .
Чтобы найти опорный план, поступим
следующим образом. Разрешающим столбцом
будет столбец под переменной
.
Выберем в качестве разрешающей строку,
в которой находится переменная
,
так как симплексное отношение в ней
наименьшее. Тогда разрешающим элементом
будет
.
Чтобы найти опорный план, поступим
следующим образом. Разрешающим столбцом
будет столбец под переменной
.
Выберем в качестве разрешающей строку,
в которой находится переменная
,
так как симплексное отношение в ней
наименьшее. Тогда разрешающим элементом
будет
![]() .
Делим разрешающую строку на (-2), -
разрешающий столбец – на
.
Делим разрешающую строку на (-2), -
разрешающий столбец – на
![]() .
Все остальные элементы вычисляем по
правилу прямоугольника. Меняем местами
переменные
и
.
Получаем таблицу 1.13.
.
Все остальные элементы вычисляем по
правилу прямоугольника. Меняем местами
переменные
и
.
Получаем таблицу 1.13.
Найден начальный
опорный план
![]() (точка
С рис. 1.12), все координаты которого
положительны. Этот план не является
оптимальным, так как в F
– строке
имеются отрицательные элементы. Делаем
шаг симплексных преобразований. Для
этого выбираем в качестве разрешающего
столбца тот, в котором наименьший
элемент, а именно (-3/2). Вычисляем
симплексные отношения. Единственное
значение в симплексном столбце, которое
даёт возможность определить разрешающую
строку это значение 2, в строке, в которой
находится неизвестная
.
Таким образом, разрешающим элементом
будет
(точка
С рис. 1.12), все координаты которого
положительны. Этот план не является
оптимальным, так как в F
– строке
имеются отрицательные элементы. Делаем
шаг симплексных преобразований. Для
этого выбираем в качестве разрешающего
столбца тот, в котором наименьший
элемент, а именно (-3/2). Вычисляем
симплексные отношения. Единственное
значение в симплексном столбце, которое
даёт возможность определить разрешающую
строку это значение 2, в строке, в которой
находится неизвестная
.
Таким образом, разрешающим элементом
будет
![]() .
.
Делаем обычные симплексные преобразования, получаем новую таблицу 1.14.
Таблица 1.14 Таблица 1.15
Б.П. |
1 |
С.П. |
С.С. |
|
Б.П. |
1 |
С.П. |
||
|
|
|
|
|
|||||
|
2 |
2/3 |
1/3 |
6 |
|
|
3/2 |
|
|
|
3 |
1/3 |
-1/3 |
- |
|
|
7/2 |
|
|
|
1 |
1/3 |
2 |
3/2 |
|
|
3/2 |
|
|
F= |
13 |
7/3 |
-1/3 |
|
|
F= |
27/2 |
5/2 |
1/2 |
Очередной опорный
план
![]() (точка
В рис.1.12). Он не является оптимальным,
так как в F
– строке
есть ещё один отрицательный элемент.
Необходимо сделать следующий шаг
симплексных преобразований. Разрешающим
столбцом будет столбец под переменной
.
Вычисляем симплексные отношения.
Наименьшим будет отношение 3/2, расположенное
в строке, где находится переменная
(точка
В рис.1.12). Он не является оптимальным,
так как в F
– строке
есть ещё один отрицательный элемент.
Необходимо сделать следующий шаг
симплексных преобразований. Разрешающим
столбцом будет столбец под переменной
.
Вычисляем симплексные отношения.
Наименьшим будет отношение 3/2, расположенное
в строке, где находится переменная
![]() .
Тогда разрешающим элементом будет
.
Тогда разрешающим элементом будет
![]() .
.
Делаем обычный
шаг симплексных преобразований, получаем
таблицу 1.15, в которой все переменные и
элементы F
– строки положительны. Значит, найден
оптимальный опорный план
![]() (точка А рис.1.12). Максимальное значение
целевой функции
(точка А рис.1.12). Максимальное значение
целевой функции
![]() .
.
Г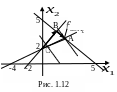 еометрическое
решение изображено на Рис.1.12. Точка С
соответствует опорному плану
.
еометрическое
решение изображено на Рис.1.12. Точка С
соответствует опорному плану
.
Точка В соответствует опорному плану .
Точка А – оптимальному опорному плану
.
Пример 10. Найти решение задачи
![]() ,
,
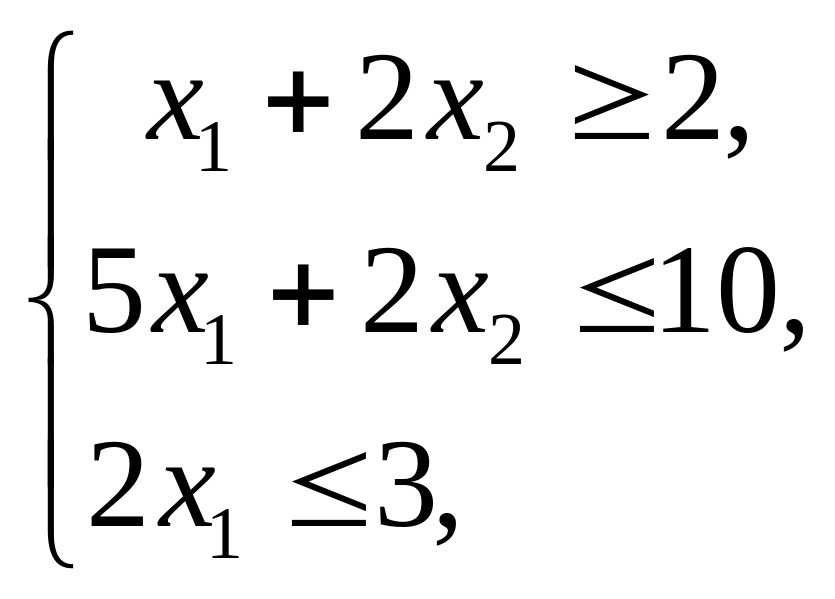
Решение. Для решения задачи используем соотношение:
![]() ,
,
тогда получим
![]()
Ограничения преобразуем к каноническому виду введением балансовых переменных
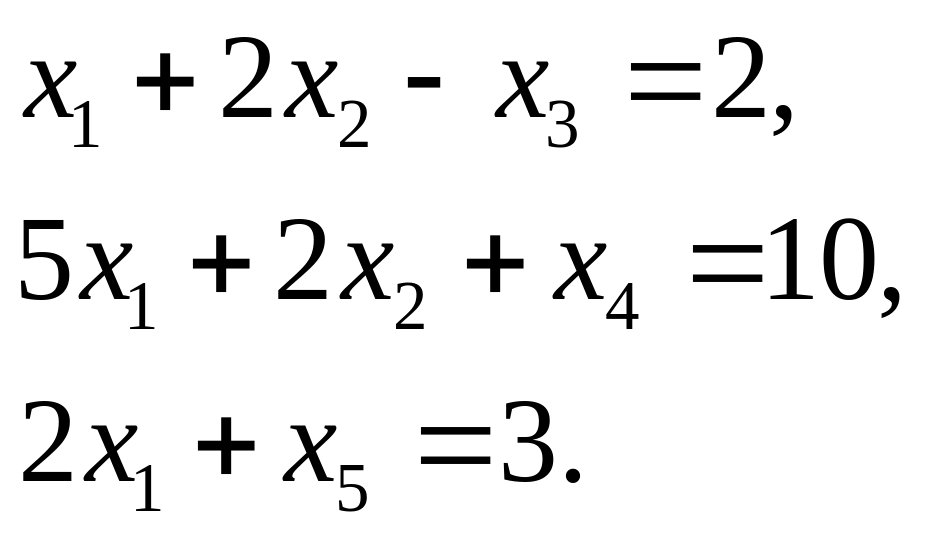
Балансовые переменные примем за базисные:
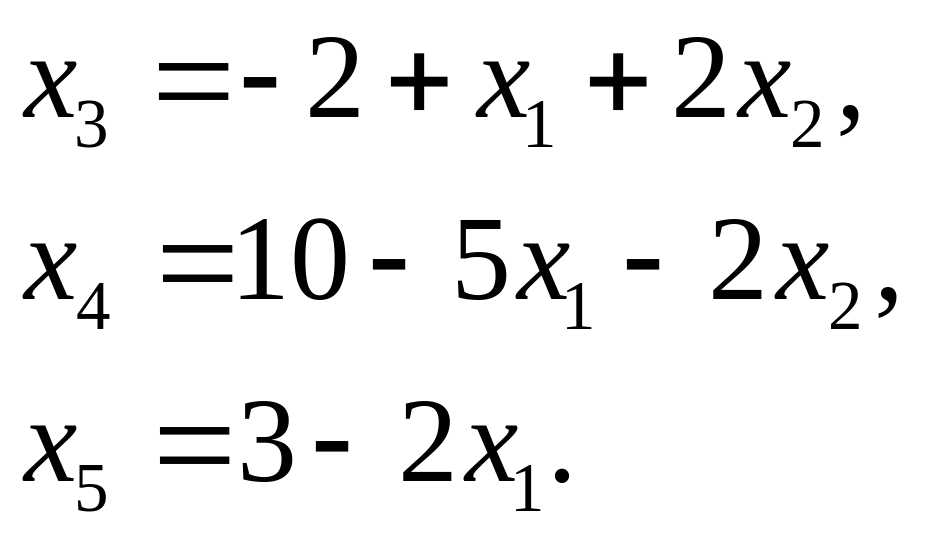
Составляем симплексную таблицу 1.16.
Таблица 1.16 Таблица 1.17
Б.П. |
1 |
С.П. |
С.С. |
|
Б.П. |
1 |
С.П. |
С.С. |
||
- |
- |
|
- |
- |
||||||
= |
-2 |
-1 |
|
1 |
|
= |
1 |
½ |
-1/2 |
2 |
= |
10 |
5 |
2 |
5 |
|
= |
8 |
4 |
1 |
2 |
= |
3 |
2 |
0 |
- |
|
= |
3 |
|
0 |
-3/2 |
|
0 |
-2 |
1 |
|
|
= |
-1 |
-5/2 |
1/2 |
|
Полученное базисное
решение не является опорным планом, так
как в нём есть отрицательный элемент
![]() .
Находим опорный план. В строке с
неизвестной величиной
,
там, где свободный член отрицательный,
находим наименьший элемент (-2), этот
столбец под неизвестной
будет разрешающим. Вычисляем элементы
симплексного столбца. Находим
.
Находим опорный план. В строке с
неизвестной величиной
,
там, где свободный член отрицательный,
находим наименьший элемент (-2), этот
столбец под неизвестной
будет разрешающим. Вычисляем элементы
симплексного столбца. Находим
![]() .
Следовательно, разрешающей строкой
будет строка, в которой находится
неизвестная
,
а разрешающим элементом будет (-2). Меняем
местами
и
.
Проделываем все вычисления одного шага
симплексных преобразований. Получаем
таблицу 1.17.
.
Следовательно, разрешающей строкой
будет строка, в которой находится
неизвестная
,
а разрешающим элементом будет (-2). Меняем
местами
и
.
Проделываем все вычисления одного шага
симплексных преобразований. Получаем
таблицу 1.17.
Полученный план
![]() является опорным, так как все координаты
его положительны, но не является
оптимальным, так как в
–
строке есть отрицательный элемент
(-5/2). Чтобы найти оптимальный план,
сделаем столбец с элементом (-5/2)
разрешающим. Вычислим симплексные
отношения. Найдём
является опорным, так как все координаты
его положительны, но не является
оптимальным, так как в
–
строке есть отрицательный элемент
(-5/2). Чтобы найти оптимальный план,
сделаем столбец с элементом (-5/2)
разрешающим. Вычислим симплексные
отношения. Найдём
![]() .
Следовательно, разрешающий элемент
будет находиться в строке, где расположена
неизвестная
.
Проделываем вычисления очередного шага
симплексных преобразований, получаем
таблицу 1.18
.
Следовательно, разрешающий элемент
будет находиться в строке, где расположена
неизвестная
.
Проделываем вычисления очередного шага
симплексных преобразований, получаем
таблицу 1.18
Таблица 1.18
|
1 |
- |
- |
= |
1/4 |
|
|
= |
2 |
|
|
= |
3/2 |
|
|
|
11/4 |
5/4 |
1/2 |
Вначале вычислим
все свободные члены и элементы
–
строки. Так как все они положительны,
то остальные элементы таблицы можно не
вычислять. Получен оптимальный опорный
план
![]() при этом значение функции
при этом значение функции
![]() .
Тогда, минимум функции f
будет
.
Тогда, минимум функции f
будет
![]() .
.



 /3
/3