
- •Задачи линейного программирования
- •Постановка задачи
- •Задачи для решения
- •1.2. Свойства решений задач линейного программирования
- •Графический метод решения задач линейного программирования Случай двух переменных
- •Случай многих переменных
- •1.4.2.Симплексный метод
- •Этап 1. Определение начального опорного плана.
- •Случай вырождения
- •Задачи для решения
- •Метод искусственного базиса
- •Задачи для решения
- •1.5. Теория двойственности в линейном программировании
- •1.5.1. Постановка задачи
- •Некоторые частные случаи
- •1.5.2. Основные теоремы двойственности
- •Задачи для решения
- •1.5.3. Геометрическая интерпретация двойственных задач
- •1.5.4. Двойственный симплекс – метод
- •Этап 1. Определение начального опорного плана (псевдоплана).
- •Этап 2. Определение оптимального плана.
- •Задачи для решения
- •1.6. Экономическая интерпретация двойственности
- •1.6.1. Анализ моделей на чувствительность.
- •Использование графического метода.
- •Использование симплекс-метода.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Использование графического метода.
- •Использование симплекс-таблицы.
- •Применение компьютера Инструкция по использованию надстройки «Поиск решения»
- •1.10. Решение задачи с использованием
Использование графического метода.
Изобразим вектор
![]() ,
граничные прямые
,
граничные прямые
х1 + х2 = 8; (L1);
4х1 + 10х2 = 40; (L2);
х1 = 4 (L3);
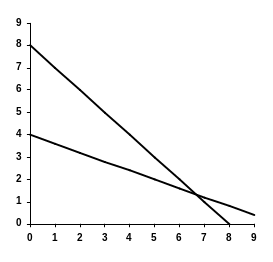
и построим многоугольник решений OABC, как показано на рис. 1.15.
L1
х2
х1
L2
L3
A
B
C
D
E
G
K
O
F


![]()

Рис. 1.15
Проведем линию
уровня прямую F.
Перпендикулярно к ней построим вектор
![]() .
Для поиска максимального значения
целевой функции перемещаем прямую F
параллельно самой себе в направлении
вектора
.
Целевая функция достигает своего
экстремума в одной из вершин многоугольника
решений.
.
Для поиска максимального значения
целевой функции перемещаем прямую F
параллельно самой себе в направлении
вектора
.
Целевая функция достигает своего
экстремума в одной из вершин многоугольника
решений.
В нашем примере максимальное значение целевой функции достигается в точке B – точке пересечения двух прямых: L2 и L3. Оптимальное решение задачи: х1 = 4, х2 = 2,4, F =15,2.
Использование симплекс-метода.
Преобразуем исходную математическую модель к каноническому виду
, (1*)
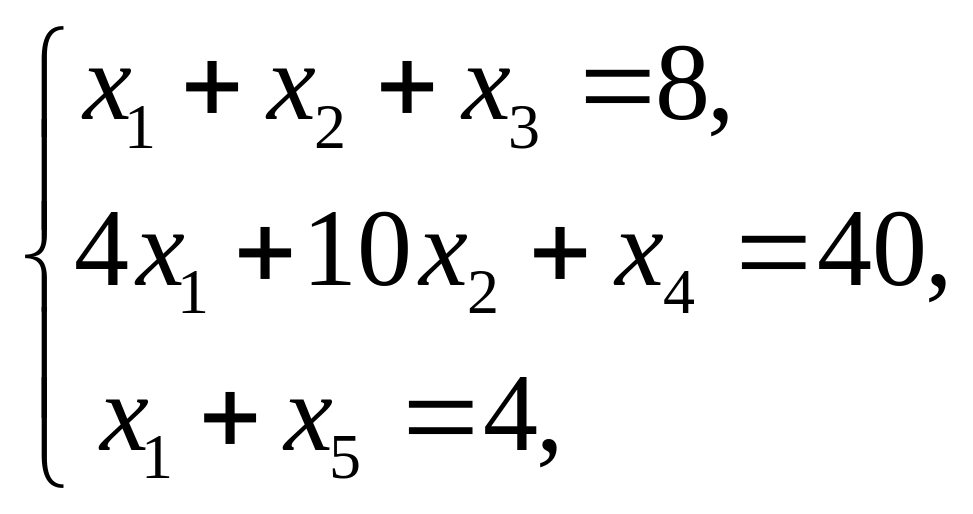 (2*)
(2*)
х1 ³ 0, х2 ³ 0, х3 ³ 0, х4 ³ 0, х5 ³ 0. (3*)
Здесь х3, х4, х5 – дополнительные балансовые (остаточные) переменные, добавленные в неравенства для преобразования их в равенства.
Допустимое базисное
решение имеет вид
![]() ,
,
![]() 0.
0.
Построим начальную симплекс-таблицу 1.36.
Решение
не является оптимальным, так как в
![]() -
строке таблицы стоят отрицательные
элементы.
-
строке таблицы стоят отрицательные
элементы.
Таблица 1.36
Б.П. |
1 |
С.П. |
||
-x1 |
-x2 |
С.С. |
||
x3 |
8 |
1 |
1 |
8/1=8 |
x4 |
40 |
4 |
10 |
40/10=4 |
x5 |
4 |
1 |
0 |
|
Fmax |
0 |
–2 |
–3 |
|
Столбец x2 выберем в качестве разрешающего, поскольку в - строке симплекс-таблицы для столбцов свободных переменных именно в нем находится наименьшее отрицательное число (–3).
Строку x4 определим в качестве разрешающей, так как ей соответствует наименьшее симплекс-отношение симплекс - столбца.
На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент, равный 10.
Делаем один шаг симплексных преобразований.
Таким образом, симплекс-таблица примет вид.
Таблица 1.37
Б.П. |
1 |
С.П. |
||
-x1 |
-x4 |
С.С. |
||
x3 |
4 |
0,6 |
–0,1 |
4/0,6=20/3 |
x2 |
4 |
0,4 |
0,1 |
4/0,4=10 |
x5 |
4 |
1 |
0 |
4/1=4 |
Fmax |
12 |
–0,8 |
0,3 |
|
Новое базисное
решение
![]() ,
,
![]() 12,
хотя и улучшает значение целевой функции
по сравнению с начальным, но не является
оптимальным, поскольку в последней
-
строке симплекс-таблицы имеется
отрицательный элемент (значение ( –0,8)
в столбце х1).
12,
хотя и улучшает значение целевой функции
по сравнению с начальным, но не является
оптимальным, поскольку в последней
-
строке симплекс-таблицы имеется
отрицательный элемент (значение ( –0,8)
в столбце х1).
Выберем столбец х1 в качестве разрешающего, как содержащий отрицательный элемент в - строке симплекс-таблицы 1.37.
Строку x5 определим в качестве разрешающей, так как ей соответствует наименьшее симплексное отношение. Делаем шаг симплексных преобразований. Получаем таблицу 1.38
Таблица 1.38
Б.П. |
1 |
С.П. |
|
-x4 |
-x5 |
||
x3 |
1,6 |
–0,1 |
–0,6 |
x2 |
2,4 |
0,1 |
–0,4 |
x1 |
4 |
0 |
1 |
F |
15,2 |
0,3 |
0,8 |
Оптимальное решение
найдено, поскольку в последней строке
симплекс-таблицы 1.38 отсутствуют
отрицательные элементы. Для небазисных
переменных значения элементов последней
строки положительны, следовательно,
задача имеет единственное оптимальное
решение
![]() ,
при этом
,
при этом
![]() 15,2.
15,2.
2. Построим математическую модель двойственной задачи (1*) - (3*).
![]() , (4*)
, (4*)
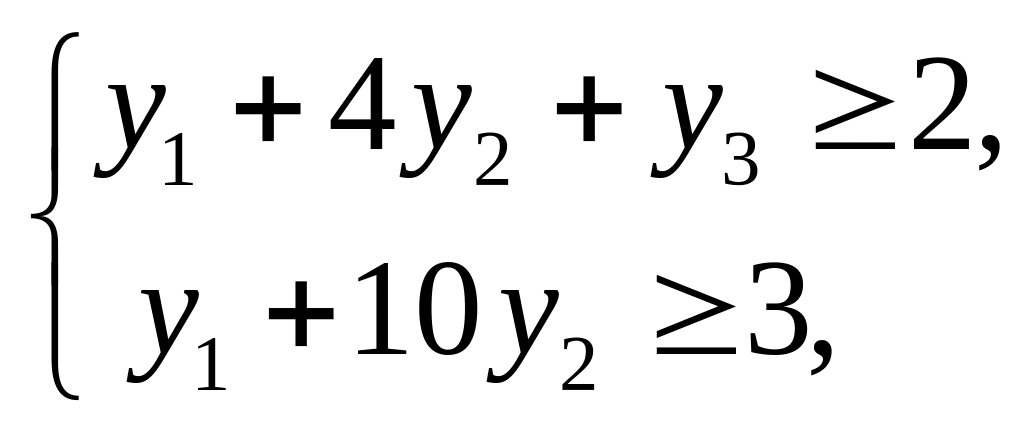 (5*)
(5*)
y1 ³ , y2 ³ 0, y3 ³ 0. (6*)
Оптимальное решение двойственной задачи можно определить на основе оптимального решения прямой задачи
Из теорем двойственности следует:
1) экстремальные значения целевых функций разрешимых прямой и двойственной задач совпадают, следовательно, 15,2;
2) компоненты оптимального плана двойственной задачи находятся в строке целевой функции итоговой симплекс-таблицы прямой задачи.
Значение переменной yi двойственной задачи соответствует теневой цене i-го ресурса прямой задачи.
При приведении
исходной задачи линейного программирования
к каноническому виду в первое неравенство,
соответствующее ресурсу Р1,
для преобразования его в равенство
добавлялась балансовая переменная х3.
Таким образом, значение переменной y1
следует искать в последней строке
итоговой симплекс-таблицы в столбце х3
и так далее. Исходя из принципа соответствия
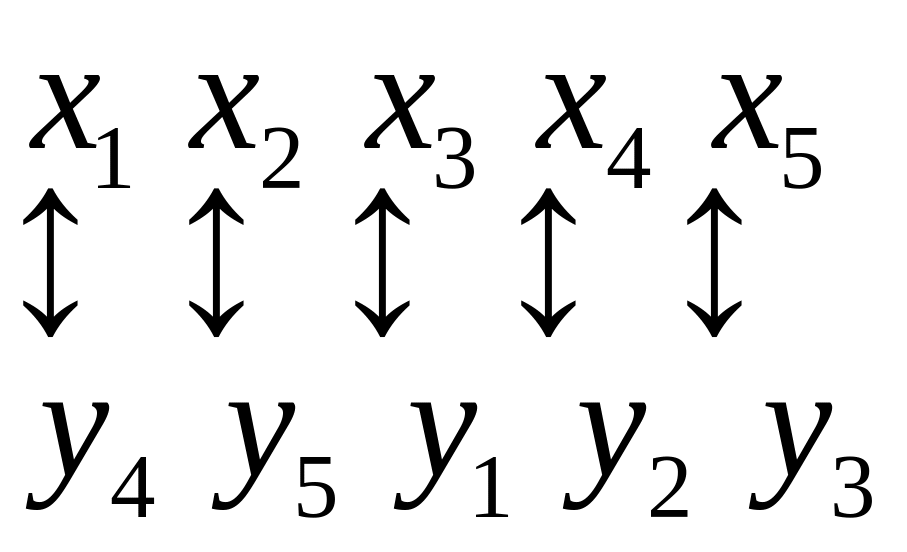 ,
находим остальные переменные. Симплексная
таблица 1.39 с двойственными решениями
будет иметь вид
,
находим остальные переменные. Симплексная
таблица 1.39 с двойственными решениями
будет иметь вид
Т аблица
1.39
аблица
1.39
Б.П. |
= |
= |
= |
|
С.П. |
С.П. Б.П. |
1 |
-x4 |
-x5 |
|
= |
1,6 |
–0,1 |
–0,6 |
|
= |
2,4 |
0,1 |
–0,4 |
|
= |
4 |
0 |
1 |
1 |
F= |
15,2 |
0,3 |
0,8 |
Оптимальное решение
двойственной задачи будет
![]() (0;0,3;0,8;0;0).
(0;0,3;0,8;0;0).
3. Определим статус ресурсов.
