Програмне забезпечення вирішення задачі
Інструкція користувача
Для реалізації цієї задачі була створена програма мовою С++. Вона є досить легка у використанні. З початку необхідно знайти файл з назвою – fs1і розширенням – txt (fs1.txt) (Рис.1).
Рис.1
В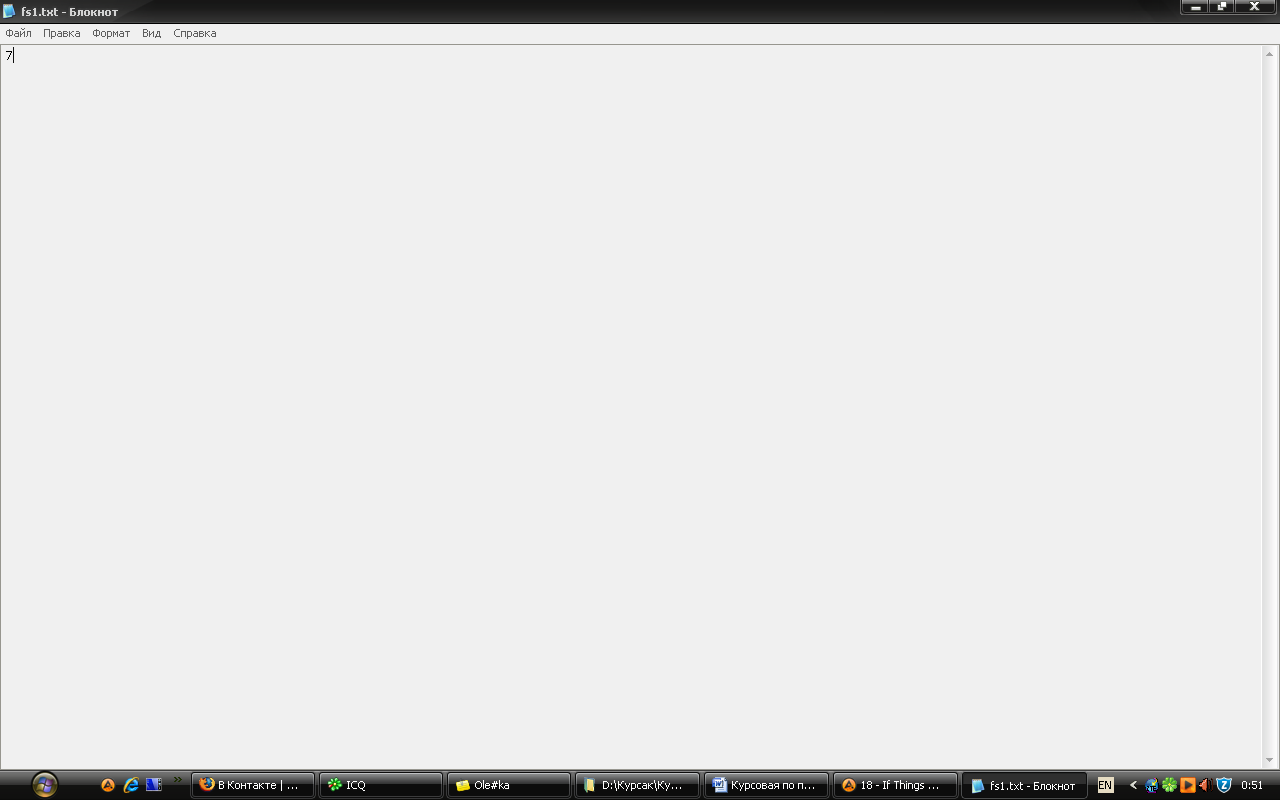
цьому файлі повинна зберігатися початкова
інформація. У першій строчці вводиться
кількість людей, що прийшли на олімпіаду,
іншими словами – кількість вершин графа
(Рис.2).
Рис.2
У наступному кроці вводиться матриця суміжності у такому вигляді (Рис.3).
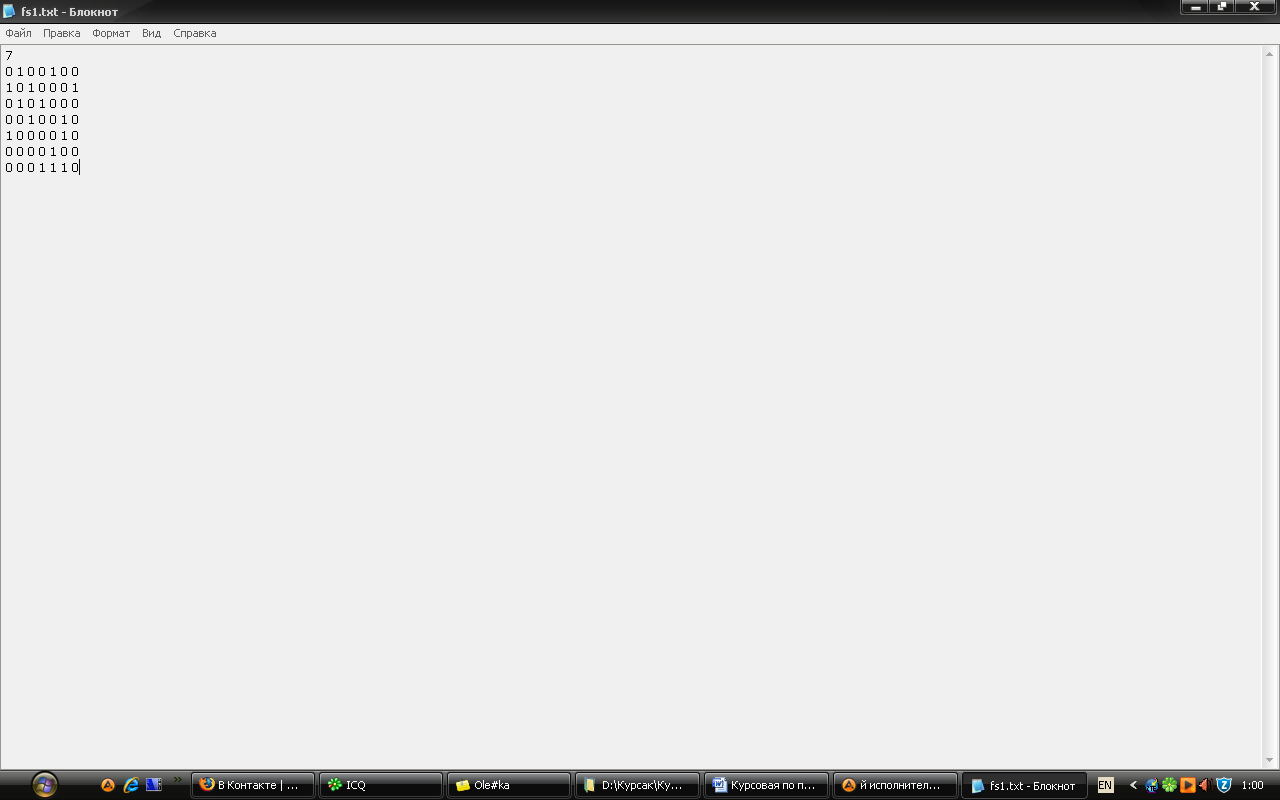
Рис.3
Далі буде безпосередній запуск програми. Закриваєте файл fs1.txt – він Вам більше не потрібен. У цій же течці шукаєте файл GRAF.exe (Рис.4).
Рис.4
Запускаєте файл GRAF.exe, він відкривається і одразу ж закривається, уся інформація про результати вирішення поміщається у файл FS2.TXT, що створюється автоматично із закінченням роботи GRAF.exe (Рис.5).
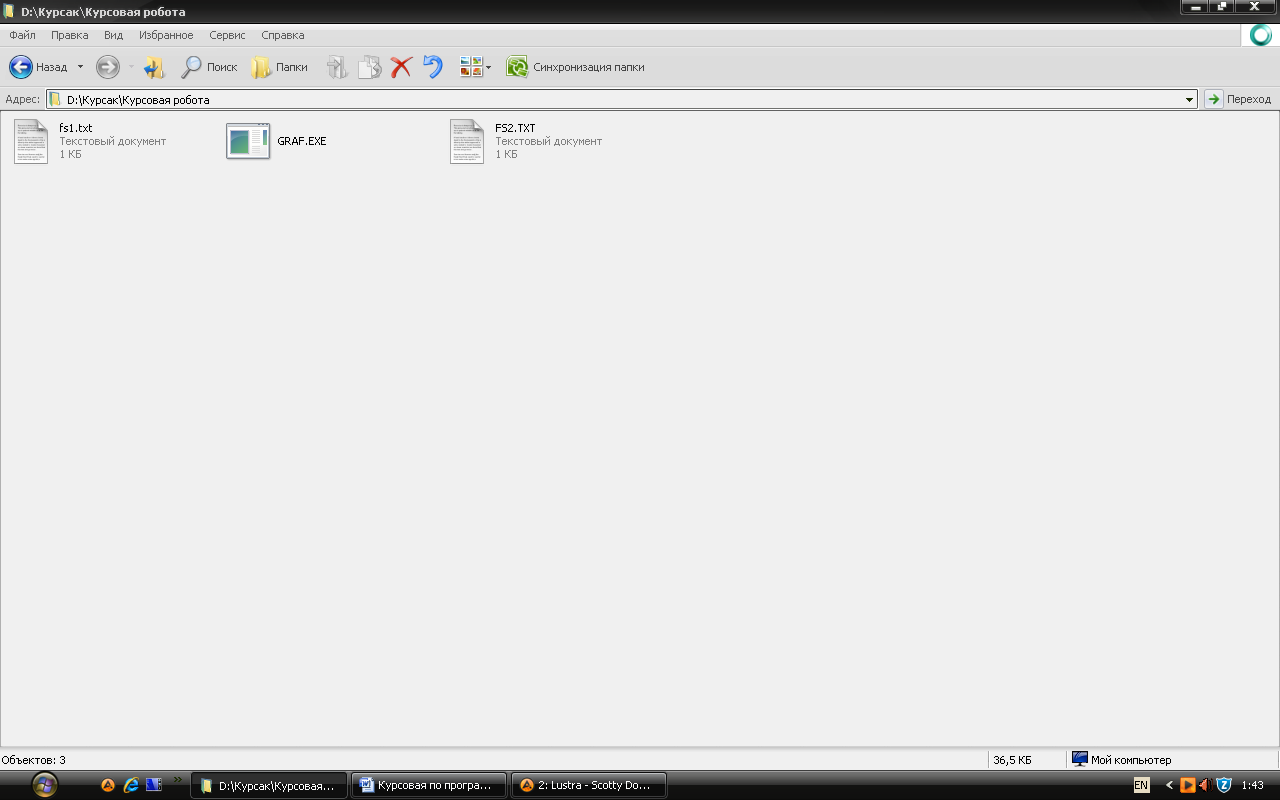
Рис.5
У файлі знаходиться відповідь на основне запитання задачі: «Чи можливо опосередковано перезнайомити їх усіх між собою?» - Yes або No, а також час початку й кінця роботи програми, відповідно (Рис.6).
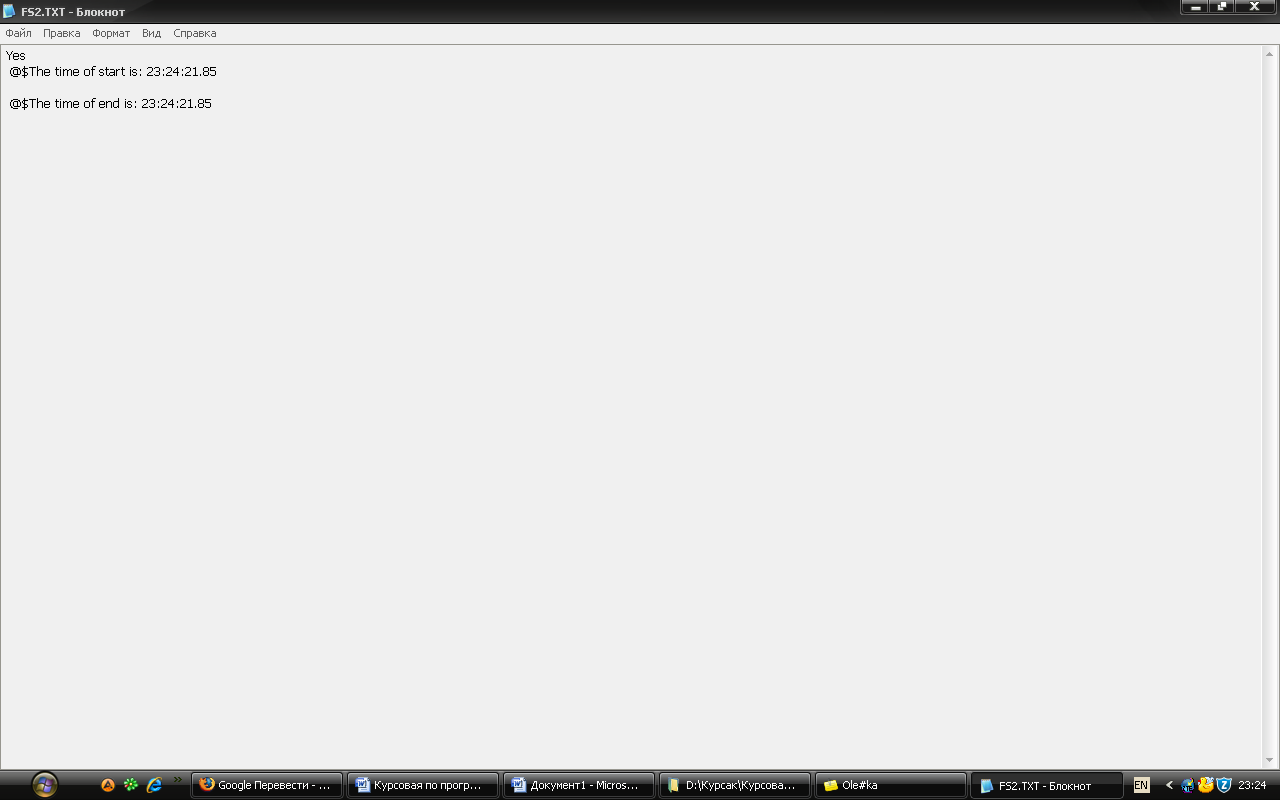
Рис.6
Відповідно, якщо у файлі знаходиться слово Yes – людей можливо перезнайомити, тобто граф – зв’язний, якщо ж No – не можливо, тобто граф – не зв’язний.
Розрахунок контрольних прикладів
№ 1. Вирішення задачі вручну. Початкові данні: N=5
Графічне зображення графа, що відображає хто із ким знайомий (Рис.7).
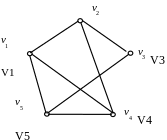V2
Рис.7
Матриця суміжності по графу:
X |
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
0 |
3 |
1 |
1 |
0 |
0 |
1 |
4 |
0 |
1 |
0 |
0 |
1 |
5 |
1 |
0 |
1 |
1 |
0 |
Виконуємо такі дії:
Помічаємо вершину №1.
X |
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
0 |
3 |
0 |
1 |
0 |
0 |
1 |
4 |
1 |
1 |
0 |
0 |
1 |
5 |
1 |
0 |
1 |
1 |
0 |
Шукаємо вершини суміжні вершині №1 – це вершини№2, №4, №5. Помічаємо їх також.
X |
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
0 |
3 |
0 |
1 |
0 |
0 |
1 |
4 |
1 |
1 |
0 |
0 |
1 |
5 |
1 |
0 |
1 |
1 |
0 |
Серед непомічених вершин шукаємо вершини суміжні вершинам №2 і №5 – це №3. Помічаємо знайдену вершину.
X |
1 |
2 |
3 |
4 |
5 |
1 |
0 |
1 |
0 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
0 |
3 |
0 |
1 |
0 |
0 |
1 |
4 |
1 |
1 |
0 |
0 |
1 |
5 |
1 |
0 |
1 |
1 |
0 |
Кількість помічених вершин дорівнює кількості вершин графа взагалі, отже граф зв'язний – всіх людей можливо перезнайомити між собою!
№2. Вирішення задачі за допомогою написаної програми.
Початкові данні містяться в файлі “fs1.txt”: N=6, матриця суміжності (Рис.8).
Рис.8
Запускаємо файл GRAF.exe й отримуємо відповідь у файлі FS2.TXT (Рис.9).
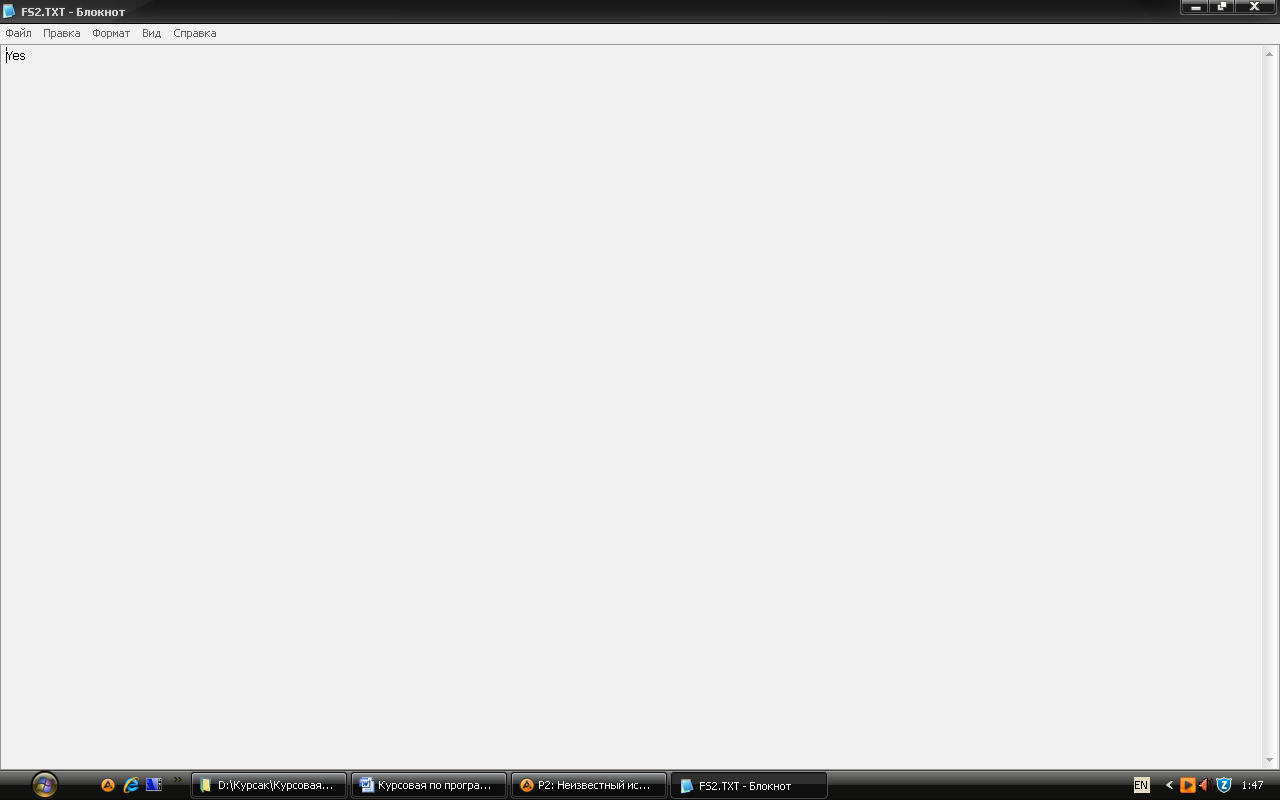
Рис.9
№3. Вирішення задачі за допомогою написаної програми.
Початкові данні містяться в файлі “fs1.txt”: N=6, матриця суміжності (Рис.10).
X |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
2 |
1 |
0 |
1 |
1 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
1 |
0 |
4 |
1 |
1 |
0 |
0 |
1 |
0 |
5 |
1 |
0 |
1 |
1 |
0 |
1 |
6 |
0 |
0 |
0 |
1 |
0 |
0 |
Рис.10
Запускаємо файл GRAF.exe й отримуємо відповідь у файлі FS2.TXT (Рис.11).
Рис.11
№4. Вирішення задачі за допомогою написаної програми.
Початкові данні містяться в файлі “fs1.txt”: N=7, матриця суміжності (Рис.12).
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
5 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
Рис.12
Запускаємо файл GRAF.exe й отримуємо відповідь у файлі FS2.TXT (Рис.13).
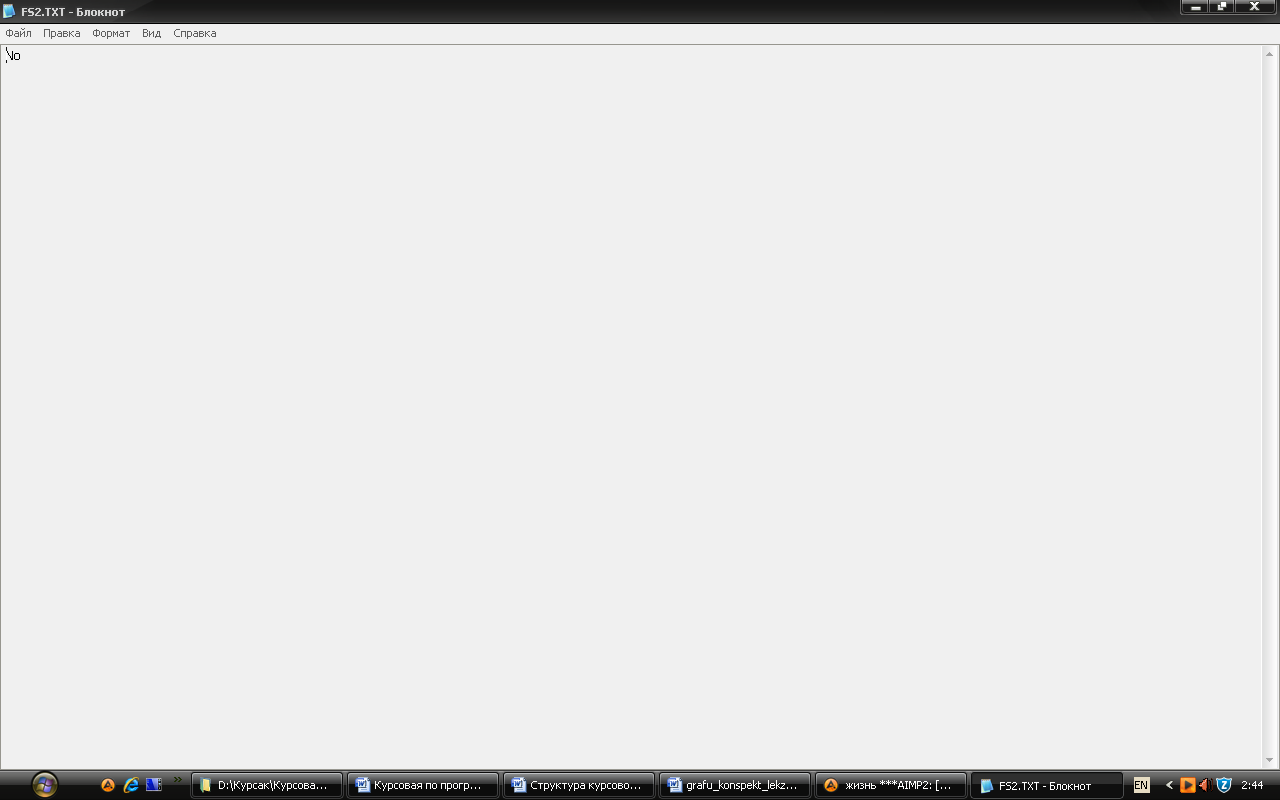
Рис.13