Задача 3.

Даны результаты тестирования для каждого из тестированных и теста длины в виде матрицы , а также вектор эталонных ответов , где – эталонный ответ на задание номер . Необходимо оценить валидность каждого задания теста.

Простейший алгоритм решения этой задачи состоит из следующих этапов.

1. Определяем для очередного задания теста по матрице количество тестированных, давших правильный ответ на -ое задание и находим их средний балл .

2. Находим аналогично количество тестированных, давших неправильный ответ на j-ое задание и их средний балл .

3. Находим дробь : знаменатель – количество тестированных, давших правильный ответ на данное задание номер , числитель – количество тестированных.

4. Находим дробь : знаменатель – количество тестированных, давших неправильный ответ на данное задание номер , числитель – количество тестированных.

5. Оцениваем дисперсию каждого -го задания и стандартное отклонение .

6. Находим стандартное отклонение 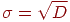по всему тесту.

7. Находим коэффициент корреляции (меру валидности задания):

8. Если 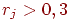, то задание считаем валидным, иначе – не валидным (отметим, что с точки зрения критериальной валидности, задания, выполненные всеми или невыполненные никем, не являются валидными).

9. Конец алгоритма.

Задача 4.

Даны результаты нормативно-ориентированного тестирования для каждого из тестированных и теста длины в виде матрицы , а также вектор эталонных ответов , где – эталонный ответ на задание номер . Необходимо оценить надежность теста (степень устойчивости результатов тестирования каждого испытуемого, если тестирование было проведено в совершенно одинаковых условиях).

Для вычисления надежности нормативно-ориентированного теста используем коэффициент корреляции между результатами двух параллельных тестов. Сравнивая коэффициенты корреляции, делаем заключение о надежности (внутренней) теста. Если две половины теста коррелированны, то и тест надёжен; в противном случае – не надёжен (или необходимо применить другой, более тонкий математический аппарат исследования надежности).

Простейший алгоритм решения этой задачи состоит из следующих этапов.

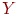1. Делим тест на две равные части и , например, по четным и нечетным номерам заданий. Этот метод называется методом расщепления теста. Таким образом, мы имеем данные по двум параллельным тестам и – индивидуальные баллы , , где – количество тестированных.

2. Для каждого задания группы выполняем предыдущий алгоритм.

3. Для каждого задания группы выполняем предыдущий алгоритм.

4. Находим коэффициент корреляции и по формуле:

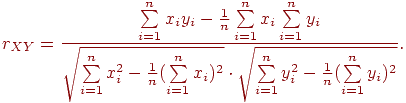
5. Находим надежность всего теста по формуле (Спирмена-Брауна):

6. Конец алгоритма.

Задача 5.

Необходимо на основе имеющихся результатов тестирования (матрица ) получить для каждого из тестированных интегральный (обобщенный) показатель выполнения теста длины , а затем по вычисленным значениям этого интегрального показателя разбить всех тестированных на заданное количество групп (задача классификации).

Алгоритм решения этой задачи состоит из следующих этапов.

1. Если для -го задания увеличение значений результатов измерения свидетельствует об улучшении соответствующего свойства, то с ним свяжем признак , а если свидетельствует об ухудшении – признак .

2. Выполняем нормирование элементов исходной матрицы так, чтобы в каждом столбце они изменялись в "одном направлении": для каждого задания (при фиксированном 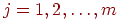) и для каждого испытуемого вычислим новое значение

где , – наибольшее и наименьшее значения элементов -го столбца и применяем преобразование вида

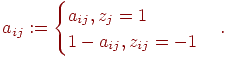
3. Для каждого столбца полученной новой матрицы (нормированной) вычисляется среднее квадратичное отклонение по формуле

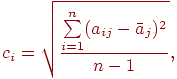
где – среднее арифметическое элементов -го столбца.

4. Вычисляется классификационный интегральный показатель

где – значение интегрального показателя для -го обучаемого , – весовой коэффициент -го задания в тесте или в банке всех заданий, – элемент матрицы или его преобразованное (нормированное, например, по отношению к максимальному элементу или к норме матрицы).

5. Находим наименьшее и наибольшее 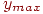значения интегрального показателя (по всем тестированным). Отрезок 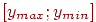делим на заданное число интервалов. Часто берут (при построении, например, гистограммы) . Всех тестированных, для которых вычисленные значения интегрального показателя попадают в один и тот же интервал, отождествляем и относим к одному классу.

6. Выдаем результаты: значения интегрального показателя для каждого тестированного, а также его класс (или классификацию тестированных по интегральному показателю).

7. Конец алгоритма.