
- •1. Предмет и задачи курса.
- •1.1 Определение эконометрики. Взаимосвязь с другими науками. Эконометрика и экономическая теория. Эконометрика и статистика. Эконометрика и экономико-математические методы.
- •Чем собственно занимается эконометрист?
- •1.2 Области применения эконометрических моделей. Методологические вопросы построения эконометрических моделей: обзор используемых методов.
- •2. Спецификация переменных в уравнениях регрессии.
- •2.1. Эконометрические модели: общая характеристика, различия статистического и эконометрического подхода к моделированию.
- •2. Регрессионные модели с одним уравнением.
- •3. Системы одновременных уравнений.
- •2.2.Спецификация переменных в уравнение регрессии. Ошибки спецификации.
- •3. Парная и множественная регрессия.
- •3.1.Понятие о функциональной, статистической и корреляционных связях. Основные задачи корреляционно-регрессионного анализа.
- •3.2. Уравнение регрессии, его смысл и назначение. Выбор типа математической функции при построении уравнения регрессии.
- •3.3 Линейная модель парной регрессии. Метод наименьших квадратов (мнк). Свойство оценок мнк.
- •Статистические свойства оценок метода наименьших квадратов.
- •Дополнительное предположение о нормальном распределении ошибок
- •Свойств выборочных вариаций (дисперсий) и ковариаций.
- •Свойства остатков
- •Несмещенность мнк-оценок
- •Состоятельность оценок
- •Эффективность (оптимальность) оценок
- •Несмещённость.
- •Эффективность.
- •Противоречия между несмещённостью и минимальной дисперсией.
- •Влияние увеличения размера выборки на точность оценок.
- •Состоятельность.
- •3.4.Ковариация. Коэффициент ковариации. Показатели качества регрессии: линейный коэффициент регрессии, коэффициент детерминации.
- •3.5.Стандартная ошибка уравнения регрессии. Оценка статистической значимости показателей корреляции, параметров уравнения регрессии. Дисперсионный анализ. Критерии Фишера и Стьюдента.
- •Интервалы прогноза по линейному уравнению регрессии.
- •3.6. Понятие о множественной регрессии. Классическая линейная модель множественной регрессии (клммр). Определение параметров уравнения множественной регрессии методом наименьших квадратов.
- •Классическая модель множественной линейной регрессии.
- •Предпосылки классической многомерной линейной регрессионной модели.
- •Выбор формы уравнения регрессии.
- •Частные уравнения регрессии
- •Множественная корреляция
- •Частная корреляция
- •3.8. Оценка качества модели множественной регрессии: f-критерий Фишера, t-критерий Стьюдента. Мультиколлинеарность. Методы устранения мультиколлинеарности.
- •Глава 4. Предпосылки метода наименьших квадратов
- •4.1. Исследование остатков величин регрессии.
- •4.2. Проблема гетероскедастичности. Её экономические причины и методы выявления.
- •4.3. Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками.
Частные уравнения регрессии
На основе линейного уравнения множественной регрессии
![]()
могут быть найдены частные уравнения регрессии:

т.е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами х при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения имеют следующий вид:

При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем:
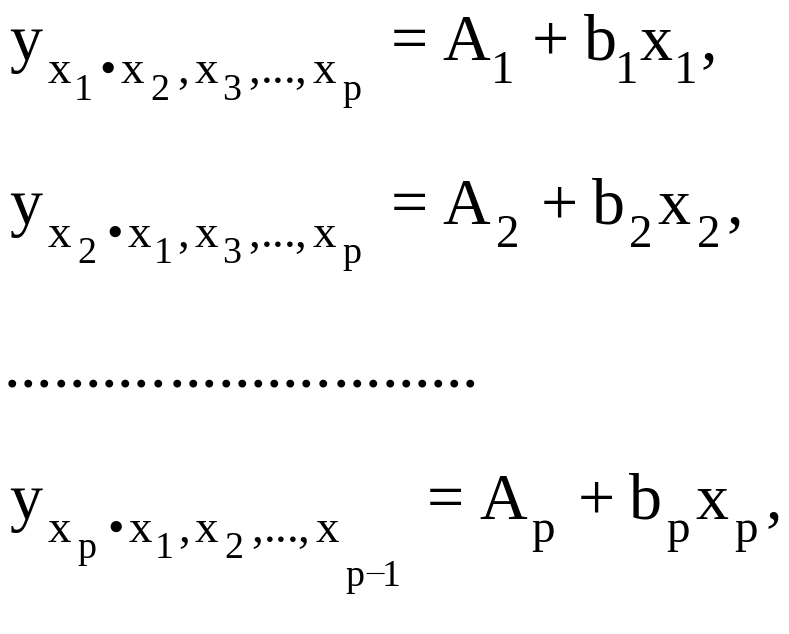
где

В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии.
Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:
 (3.4)
(3.4)
где bi – коэффициенты регрессии для фактора хi в уравнении множественной регрессии;
![]() – частное уравнение
регрессии.
– частное уравнение
регрессии.
Пример. Предположим, что по ряду регионов множественная регрессия величины импорта на определенный товар у относительно отечественного его производства х1, изменения запасов х2 и потребления на внутреннем рынке х3 оказалась следующей:
![]()
При этом средние значения для рассматриваемых признаков составили:
![]()
На основе данной информации могут быть найдены средние по совокупности показатели эластичности:
![]() (3.5)
(3.5)
Для данного примера они окажутся равными:
![]()
т.е. с ростом величины отечественного производства на 1% размер импорта в среднем по совокупности регионов возрастает на 1,053% при неизменных запасах и потреблении семей.
Для второй переменной коэффициент эластичности составляет:
![]()
т.е. с ростом изменения запасов на 1% при неизменном производстве и внутреннем потреблении величина импорта увеличивается в среднем на 0,056%.
Для второй переменной коэффициент эластичности составляет:
![]()
т.е. при неизменном объеме производства и величины запасов с увеличением внутреннего потребления на 1% импорт товар возрастает в среднем по совокупности регионов на 1,987%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. В рассматриваемом примере наибольшее воздействие на величину импорта оказывает размер внутреннего потребления товара х3, а наименьшее – изменение запасов х2.
Наряду со средними показателями эластичности в целом по совокупности регионов на основе частных уравнений регрессии могут быть определены частные коэффициенты эластичности для каждого региона. Частные уравнения регрессии в нашем случае составят:
![]()
т.е.
![]()
![]()
![]()
т.е.
![]()
![]()
![]()
т.е.
![]()
![]()
Подставляя в данные
уравнения фактические значения по
отдельным регионам соответствующих
факторов, получим значения моделируемого
показателями
![]() при заданном уровне одного значения и
средних значениях других факторов. Эти
расчетные значения результативного
признака используются для определения
частных коэффициентов по приведенной
выше формуле. Так, если, например, в
регионе х1=160,2;
х2=4,0;
х3=190,5,
то частные коэффициенты эластичности
составят:
при заданном уровне одного значения и
средних значениях других факторов. Эти
расчетные значения результативного
признака используются для определения
частных коэффициентов по приведенной
выше формуле. Так, если, например, в
регионе х1=160,2;
х2=4,0;
х3=190,5,
то частные коэффициенты эластичности
составят:
![]()
![]()
![]()
Как видим, частные коэффициенты эластичности для региона несколько отличаются от аналогичных средних показателей по совокупности регионов. Они могут быть использованы при принятии решений относительно развития конкретных регионов.
