
- •Постановка задачи
- •Построение математической модели в пространстве состояний
- •Переход от модели в пространстве состояний к модели «вход-выход»
- •Построение эквивалентной дискретной модели
- •Переход к модели «вход-выход» дискретного объекта
- •Уравнения свёртки и импульсные переходные функции
- •Операторный подход
Операторный подход
Выходной сигнал любой системы можно рассматривать как результат действия некоторого оператора:
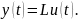
На рассматриваемые операторы накладывается 2 ограничения:
Причинность, т.е.
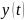 не может зависеть от
не может зависеть от
 при
при
 .
.Ограниченность.

где
 – ИПФ. Для оценки нужно рассмотреть
норму.
– ИПФ. Для оценки нужно рассмотреть
норму.
Нормы сигналов
Сигнал
измерим
на интервале
 .
Определим три основные нормы:
.
Определим три основные нормы:
 :
:

 – пространство ограниченных функций:
– пространство ограниченных функций:

 :
:

Нормы операторов
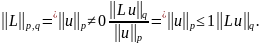

 ,
т.е.
,
т.е.
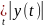 ;
;
Для дискретных объектов и систем будем обозначать соответствующие пространства:
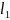 :
:
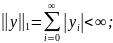
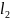 :
:
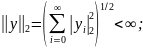
 :
:

Нормы передаточных функций
Рассмотрим матрицу
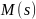 размера
размера
 ,
элементы которой – это аналитические
выражения комплексной переменной
,
элементы которой – это аналитические
выражения комплексной переменной
 в правой полуплоскости (т.е.
в правой полуплоскости (т.е.
 ).
Все полюса устойчивой системы
находятся в левой полуплоскости. Тогда:
).
Все полюса устойчивой системы
находятся в левой полуплоскости. Тогда:

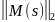 – спектральная норма матрицы
:
– спектральная норма матрицы
:

где
 – комплексно сопряжённая матрица.
Выражение под корнем – это максимальное
сингулярное число. В силу того, что
функция аналитическая, максимальное
значение достигается на границе (на
мнимой оси).
– комплексно сопряжённая матрица.
Выражение под корнем – это максимальное
сингулярное число. В силу того, что
функция аналитическая, максимальное
значение достигается на границе (на
мнимой оси).
Если
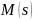 – скалярная передаточная функция, то
– скалярная передаточная функция, то

 – амплитудно-частотная характеристика.
– амплитудно-частотная характеристика.
Для устойчивых систем выполняется
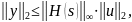

 показывает, во сколько раз может
измениться энергия сигнала при прохождении
через систему.
показывает, во сколько раз может
измениться энергия сигнала при прохождении
через систему.
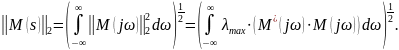
Если – скаляр, то

Вычислим вторую норму и норму-бесконечность передаточных функций непрерывной и дискретной моделей. Воспользуемся функцией Matlab:
norm(H,2)
ans =
0.1759
norm(H,inf)
ans =
1.4142
norm(Hd,2)
ans =
0.2478
norm(Hd,inf)
ans =
1.4142
Ранее говорилось, что норма-бесконечность показывает, во сколько раз может измениться сигнал при прохождении через систему. Полученные результаты говорят о том, что сигнал на выходе рассматриваемой системы может отличаться в 1,5 раза от сигнала на входе.
