Тема №7: Закон распределения. Характеристики рядов распределения.

7.1. Закономерности распределения.

В вариационных рядах существует связь в изменении частот и значении варьируемого признака, с увеличением варьирующего признака величина частот вначале возрастает до определенной величины, а затем уменьшается. Такие изменения называются закономерностями распределения.

Рассеивание кривой распределения по оси абсцисс является показателем колеблемости признака. На практике сталкиваются с различными видами распределений при изучении однородных совокупностей.

Изучение закономерности (формы распределения) включает решение следующих задач:

- выяснение общего характера распределения;

- выражение эмпирического распределения;

- проверка соответствия найденного теоретического распределения эмпирическому.

Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей ассиметрии и эксцесса.

Для однородной совокупности характерно одновершинное распределение. Появление двух и более вершин требует перегруппировки данных для получения более однородных совокупностей.

7.2. Характеристики рядов распределения.

Для выяснения однородности и общего характера распределения необходимо вычислить показатели ассиметрии и эксцесса.

Симметричным называется распределение, в котором частоты любых 2-х вариантов, равностоящих от центра распределения равны между собой.

Для симметричных распределений средняя арифметическая, мода, медиана равны между собой.

Для оценки используется коэффициент ассиметрии, который выражается соотношением:

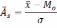
Величина A_s может быть положительной (указывает на наличие правосторонней ассиметрии), отрицательной (левосторонняя ассиметрия).

При правосторонней ассиметрии выполняется условие:

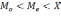
Первый график правосторонняя ассиметрия, второй – левосторонняя.

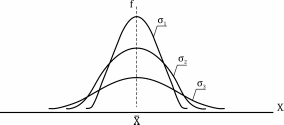
При левосторонней ассиметрии:

Ассиметрия считается существенной если выполняется соотношение:

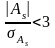
При этом среднеквадратическое отклонение рассчитывается по формуле:

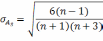
Для симметричных распределений используется показатель эксцесса:

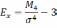
Оценка существенности показателей ассиметрии и эксцесса позволяет определить можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения.

7.3. Нормальный закон распределения

Для построения кривой нормального закона распределения необходимо знать среднее значение и среднеквадратическое отклонение.

Уравнение нормальной кривой:

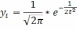
Где – ордината кривой нормального распределения;

t – нормированное отклонение:

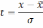
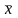
- арифметическая средняя распределения.

Особенности кривой нормального распределения:

- кривая симметрична максимальной ординаты, которой соответствует значение х=Мо=Ме и её величина будет равна 1/ ;

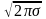- кривая приближается к оси абсцисс до бесконечности;

- кривая имеет две точки перегиба, находящиеся на расстоянии 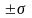от ;

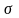- при с увеличением кривая становится более пологой;

- при находится 68,3 % всех значений признака;

- при 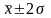находится 95,4 % всех значений признака;

- при 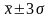находится 99,7 % всех значений признака.

Нормальное распределение возможно если на величину признака влияет большое число случайных величин. Для удобства вычислений случайная величина нормируется. Величина 1/ 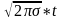называется нормированной функцией.

Для нормированной случайной величины математическое ожидание равно 0, а дисперсия равна 1. Тогда определенный интеграл вида:

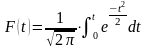называется нормированной функцией Лапласа и характеризует площадь от кривой в интервале от 0 до t.

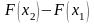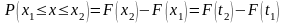Для того, чтобы оценить вероятность попадания в интервал от - до х рассматривается функция . Для определения попадания х в интервал от х1 до х2 необходимо вычислить разность , т.е. необходимо определить вероятность того, что х находится в интервале х1 и х2 , где .