Контрольные работы по Математике Преподаватель: проф. Мухарлямов Р.Г.

Курс: Первый Семестр: II Специальность: 220400 С и С А Т П

Заочное отделение Группы: 3122, 23 (после колледжа)________

30

Вариант:

Тема: " Интегральное исчисление функций одной переменной "

Задание 1. Вычислить неопределенные интегралы:

а) б) ; в) г)

Задание 2. Найти неопределенные интегралы: а) б) .

Задание 3. Вычислить определенные интегралы: а) б)

Задание 4. Вычислить площадь фигуры, ограниченной линиями:

а) ; б) ; в) .

Задание 5. Вычислить длину дуги кривой: .

Задание 6. Вычислить объем тела, образованного вращением фигуры вокруг оси ОХ:

.

Задание 7. Вычислить несобственные интегралы или доказать их сходимость или расходимость:

а) б)

Задание 8. Изменить порядок интегрирования в двойном интеграле: Задание 9. Вычислить объем тела, ограниченного заданными поверхностями:

х² + у² = 4, у + 2z – 4 = 0, z = 0.

Тема: " Интегральное исчисление функций одной переменной "

Задание 1. Вычислить неопределенные интегралы:

а) б) в) г)

Задание 2. Найти неопределенные интегралы: а) б) .

Задание 3. Вычислить определенные интегралы: а) б)

Задание 4. Вычислить площадь фигуры, ограниченной линиями:

а) ; б) ; в) .

Задание 5. Вычислить длину дуги кривой: .

Задание 6. Вычислить объем тела, образованного вращением фигуры вокруг оси ОХ:

.

Задание 7. Вычислить несобственные интегралы или доказать их сходимость или расходимость:

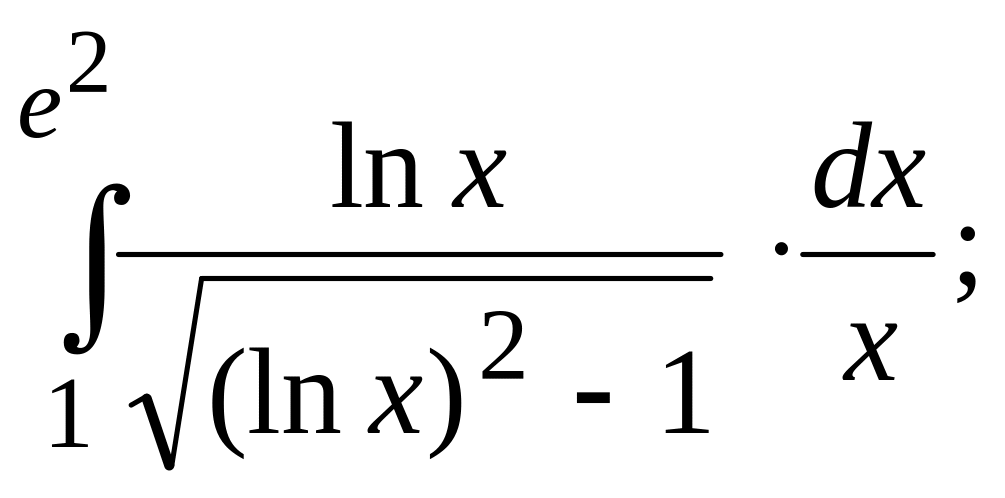а) б)

Задание 8. Изменить порядок интегрирования в двойном интеграле:

Задание 9. Вычислить объем тела, ограниченного заданными поверхностями:

х² + у² = 1, у + 2z + 2 = 0, z = 0.

Тема: " Интегральное исчисление функций одной переменной "

Задание 1. Вычислить неопределенные интегралы:

а) б) в) г)

Задание 2. Найти неопределенные интегралы: а) б) .

Задание 3. Вычислить определенные интегралы: а) б)

Задание 4. Вычислить площадь фигуры, ограниченной линиями:

а) ; б) ; в) .

Задание 5. Вычислить длину дуги кривой: .

Задание 6. Вычислить объем тела, образованного вращением фигуры вокруг оси ОХ:

.

Задание 7. Вычислить несобственные интегралы или доказать их сходимость или расходимость:

а) б)

Задание 8. Изменить порядок интегрирования в двойном интеграле:

Задание 9. Вычислить объем тела, ограниченного заданными поверхностями:

х² + у² = 4, у – 2z + 4 = 0, z = 0.

Тема: " Интегральное исчисление функций одной переменной "

Задание 1. Вычислить неопределенные интегралы:

а) б) в) г)

Задание 2. Найти неопределенные интегралы: а) б) .

Задание 3. Вычислить определенные интегралы: а) б)

Задание 4. Вычислить площадь фигуры, ограниченной линиями:

а) ; б) ; в) .

Задание 5. Вычислить длину дуги кривой: .

Задание 6. Вычислить объем тела, образованного вращением фигуры вокруг оси ОХ: .