Лабораторная работа №7 Явление резонанса в колебательном контуре

Цель работы: изучение зависимости тока в колебательном контуре от частоты источника ЭДС, включенного в контур, и измерение резонансной частоты контура.

В ведение

Рассмотрим процессы, протекающие в колебательном контуре, подключенном к источнику, ЭДС которого изменяется по гармоническому закону:

, (11.1)

где U – напряжение на контуре емкостью C; I – ток в контуре.

Полагаем, что мгновенные значения токов и напряжений удовлетворяют законам, установленным для цепей постоянного тока. Такие токи называются квазистационарными. В любой момент времени сумма падений напряжения на элементах цепи равны ЭДС (рис11.1):

. (11.2)

Падение напряжения на катушке индуктивностью L

, (11.3)

ток в катушке и контуре

. (11.4)

Подстановка (11.3) и (11.4) в (11.2) дает

. (11.5)

Разделим это уравнение на LC и введем обозначения:

; .

Обозначая дифференцирование по времени точкой, получим дифференциальное уравнение

. (11.6)

Его решение дает закон изменения напряжения на конденсаторе с течением времени и равно сумме полного решения однородного уравнения (11.7) и частного решения уравнения (11.6):

(11.7)

Однородное уравнение (11.7) имеет решение

, (11.8)

являющееся уравнением затухающих колебаний. Затухание определяется членом е^-βt. За время амплитуда колебаний уменьшается в е раз. Затухание в колебательном контуре связано с превращением энергии колебаний в джоулево тепло в сопротивлении R. При составляющая U₁ решения уравнения (11.6) исчезнет, следовательно, она отражает переходный процесс, определенный начальными условиями и параметрами контура. Установившиеся колебания в цепи происходят с частотой Ω и возможным сдвигом по фазе. Поэтому решение ищут в виде

, (11.9)

где U₀ и φ подлежат определению.

Подстановка (11.9) в (11.6) дает:

; (11.10)

. (11.11)

Таким образом, амплитуда и фаза напряжения на конденсаторе зависят от соотношения частоты источника ЭДС Ω и частоты ω₀.

Ток в контуре , где . Амплитуда тока в контуре также зависит от соотношения частот Ω и :

(11.12)

График зависимости от представлена на рисунке 11.2.

И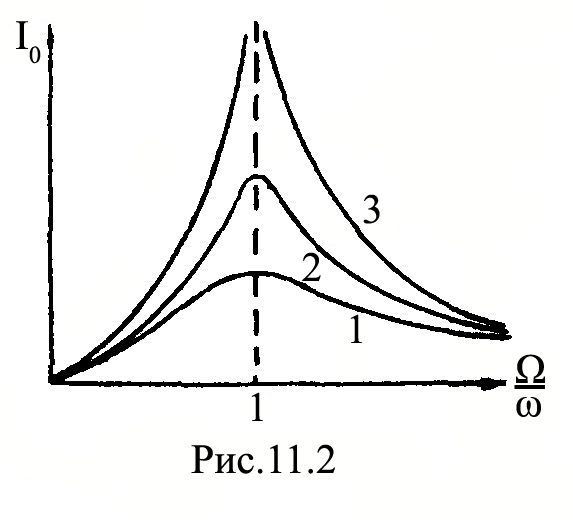 з графика видно, что амплитуда тока резко возрастает при приближении циклической частоты Ω источника ЭДС к частоте . Это явление называется резонансом, а кривые – резонансными кривыми. Величина максимума зависит от β: при β=0 (кривая 3); при увеличении β максимальное значение уменьшается (кривые 2 и 1), определяет разность фаз колебаний тока в контуре и внешней ЭДС:

(11.13)

график зависимости от частоты представлена на рисунке 11.3.

Кривые 1 и 2 соответствуют разным значениям β. При и .

Величина , где , называется добротностью колебательного контура. Добротность контура связана с остротой резонансных кривых. Найдем ширину резонансной кривой на высоте (рис. 11.4).

.

Из формулы (11.12) следует, что максимальное значение силы тока

а,

(11.14)

При формула (11.14) запишется

(11.15)

Выражение (11.15) можно преобразовать к виду или . Величина , а вблизи резонанса . После подстановки получим :

(11.16)

При малом затухании и относительная ширина резонансной кривой численно равна величине обратной добротности контура.

Если известны параметры контура, добротность может быть рассчитана по соотношению

. (11.16а)