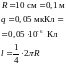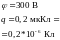- •9*. Ответ: .
- •4*. Составим полную систему уравнений для нахождения искомой величины :
- •9*. Ответ:
- •4*. Составим полную систему уравнений для нахождения искомой величины :
- •9*. Ответ:
- •4*. Составим полную систему уравнений для нахождения искомой величины :
- •4*. Составим полную систему уравнений для нахождения искомой величины :
- •9*. Ответ:
- •9*. Ответ: .
- •9. Ответ: , , ,
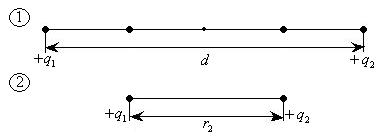
Задача 1
Точечные
заряды
 ,
,
 находятся
на расстоянии
находятся
на расстоянии
 друг
от друга. Определить напряженность поля
в точке, удаленной на
друг
от друга. Определить напряженность поля
в точке, удаленной на
 от
первого и на
от
первого и на
 от
второго заряда. Определить также силу
от
второго заряда. Определить также силу
 ,
действующую в этой точке на точечный
заряд
,
действующую в этой точке на точечный
заряд
 .
.
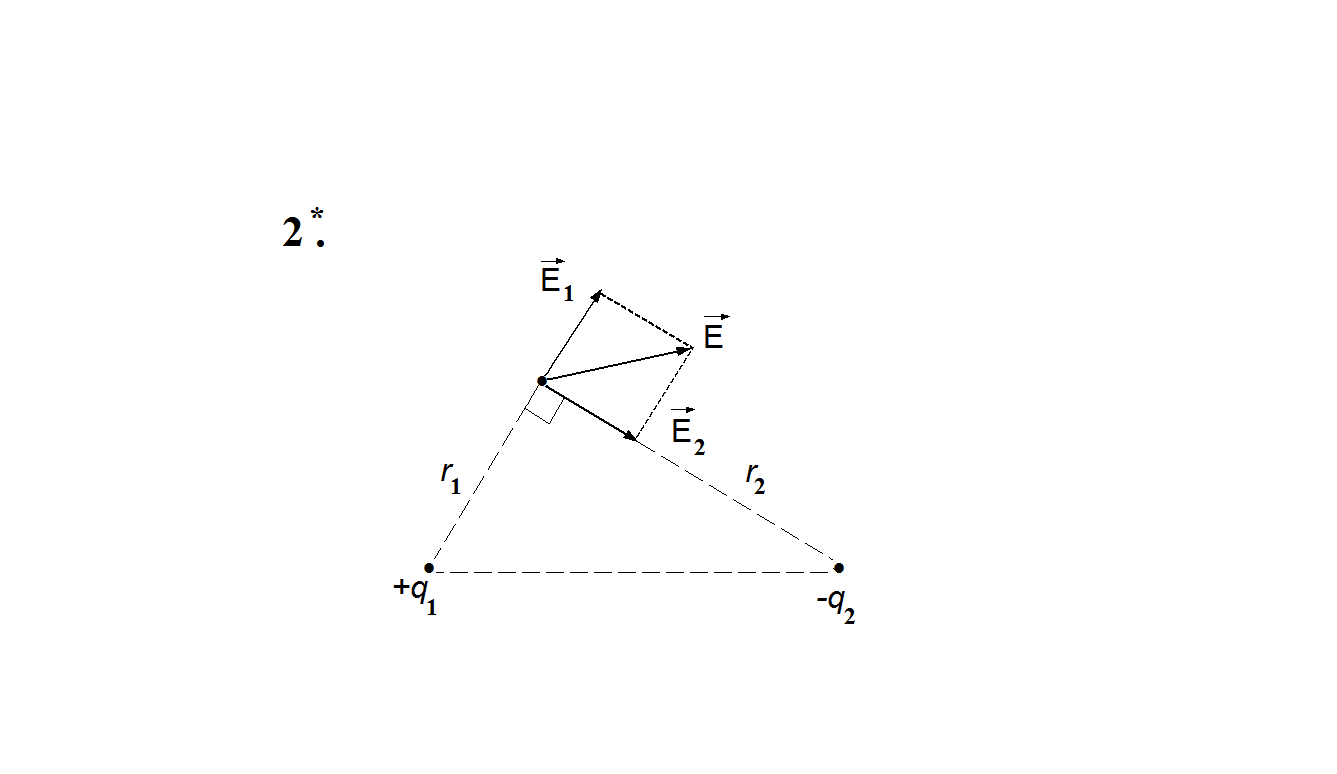
1* Дано: СИ: Решение:
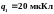



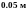


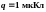

 -
?
-
?
 -
?
-
?
4*. Составим полную систему уравнений для нахождения искомой величины и уравнения для нахождения искомой величины .

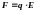
Система
трех уравнений (1)-(3) замкнута, т.к. содержит
три неизвестные величины:
 ,
,
 ,
,
 .
.
9*.
Ответ:
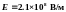 ;
;
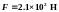 .
.
Задача 2
Три
одинаковых точечных заряда
 находятся
в вершинах равностороннего треугольника
со сторонами
находятся
в вершинах равностороннего треугольника
со сторонами
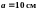 .
Определить модуль и направление силы
,
действующей на один из зарядов со стороны
двух других.
.
Определить модуль и направление силы
,
действующей на один из зарядов со стороны
двух других.
1* Дано: СИ: Решение:
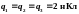

-?
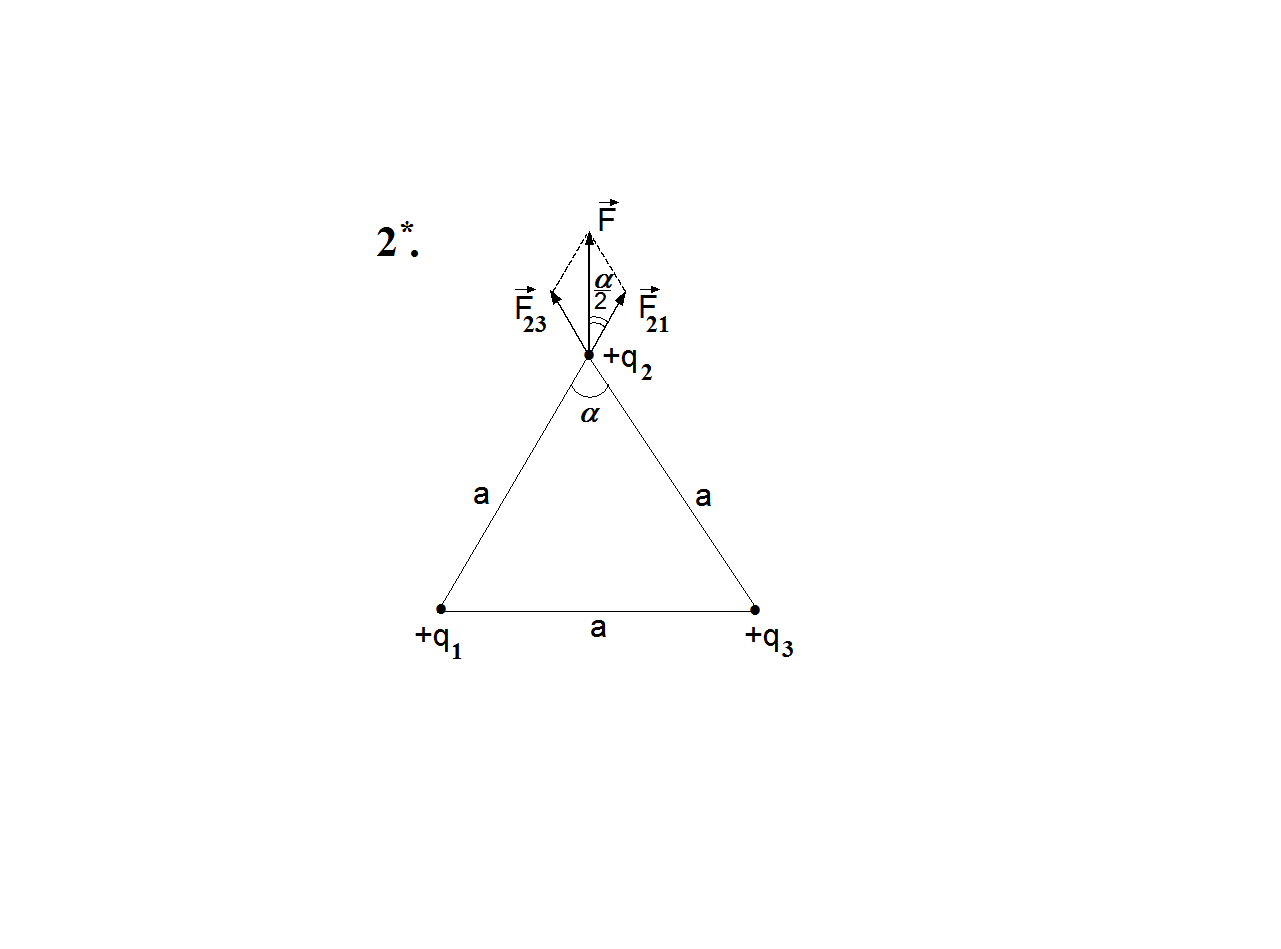
4*. Составим полную систему уравнений для нахождения искомой величины :

Система
двух уравнений (1)-(2) замкнута, так как
содержит 2 неизвестные величины:
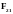 ,
,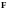 .
.
9*.
Ответ:
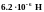
Задача 3
Два
одинаково заряженных шарика подвешены
в одной точке на нитях одинаковой длины.
При этом нити разошлись на угол
 .
Шарики погружают в масло. Какова плотность
.
Шарики погружают в масло. Какова плотность
 масла, если угол расхождения нитей при
погружении в масло остается неизменным?
Плотность материала шариков
масла, если угол расхождения нитей при
погружении в масло остается неизменным?
Плотность материала шариков
 , диэлектрическая проницаемость масла
, диэлектрическая проницаемость масла
 .
.
9.
Ответ:
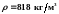
Задача 4
Четыре
одинаковых заряда
 закреплены
в вершинах квадрата со стороной
закреплены
в вершинах квадрата со стороной
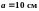 .
Найти силу
,
действующую на один из этих зарядов со
стороны трех остальных.
.
Найти силу
,
действующую на один из этих зарядов со
стороны трех остальных.
9.
Ответ:
 .
.
Задача 5
Точечные
заряды
 и
и
 находятся на расстоянии
находятся на расстоянии
 друг
от друга. Определить напряженность
электрического поля
в точке, удаленной от первого заряда на
расстояние
друг
от друга. Определить напряженность
электрического поля
в точке, удаленной от первого заряда на
расстояние
 ,
а от второго – на
,
а от второго – на
 .
.
9.
Ответ:
 .
.
Задача 6
В
вершинах правильного треугольника со
стороной
находятся заряды
 ,
,
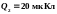 и
и
 .
Определить силу
,
действующую на заряд
.
Определить силу
,
действующую на заряд
 со стороны двух других зарядов.
со стороны двух других зарядов.
9.
Ответ:

Задача 7
В
вершинах квадрата находятся одинаковые
заряды
 .
Какой отрицательный заряд
.
Какой отрицательный заряд
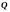 нужно поместить в центре квадрата, чтобы
сила взаимного отталкивания положительных
зарядов была уравновешена силой
притяжения отрицательного заряда?
нужно поместить в центре квадрата, чтобы
сила взаимного отталкивания положительных
зарядов была уравновешена силой
притяжения отрицательного заряда?
9.
Ответ:

Задача 8
На
расстоянии
находятся два точечных заряда:
 и
и
 .
Определить силу
,
действующую на заряд
.
Определить силу
,
действующую на заряд
 ,
удаленный от обоих зарядов на одинаковое
расстояние, равное
,
удаленный от обоих зарядов на одинаковое
расстояние, равное
 .
.
9.
Ответ:
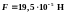 .
.
Задача 9
Тонкий
стержень длиной
 несет равномерно распределенный заряд
несет равномерно распределенный заряд
 .
Определить напряженность
.
Определить напряженность
1 *.
Дано: Решение:
*.
Дано: Решение:
 2*.
2*.

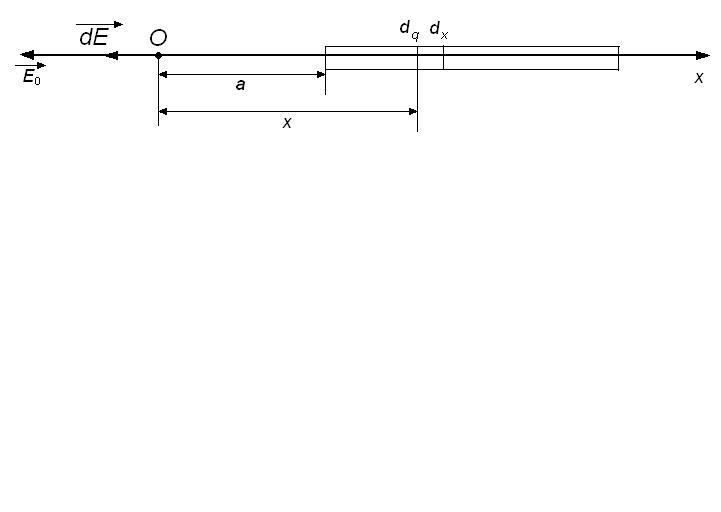
4*.
Составим
полную систему
уравнений для
нахождения искомой величины
 :
:
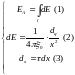
Решение
системы получается подстановкой (2) и
(3) в (1) и интегрированием по
 в
пределах от а до
в
пределах от а до .
.
9*.
Ответ:
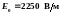
Задача 10
Бесконечный
тонкий стержень, ограниченный с одной
стороны, несет равномерно распределенный
заряд с линейной плотностью
 .
Определить напряженность
.
Определить напряженность
 электрического поля, создаваемого
распределенным зарядом в точке А,
лежащейся на оси стержня на расстоянии
электрического поля, создаваемого
распределенным зарядом в точке А,
лежащейся на оси стержня на расстоянии
 от его конца.
от его конца.
1 *.
Дано: Решение: 2*.
*.
Дано: Решение: 2*.



4*.
Составим полную
систему уравнений
для нахождения искомой величины
 :
:
Решение
системы получается подстановкой (2) и
(3) в (1) и интегрированием по x
в пределах от а до
 .
.
9*.
Ответ .
.
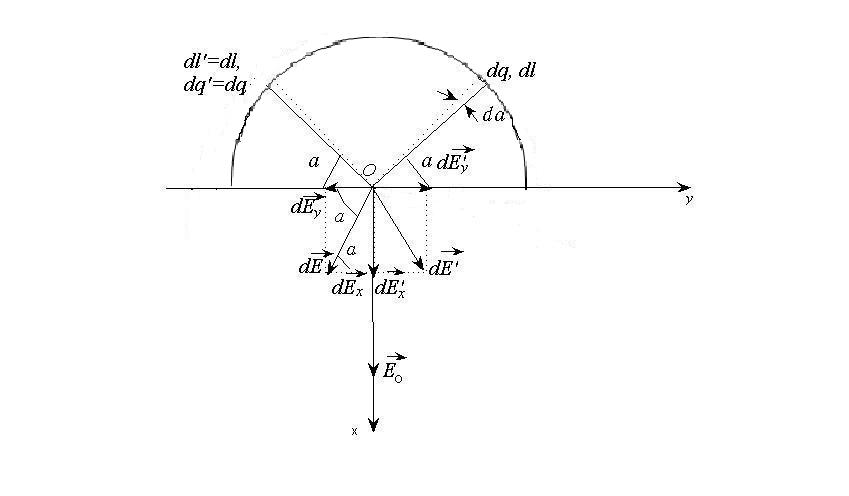
Задача 11
По
тонкому полукольцу радиуса
 равномерно распределен заряд с линейной
плотностью
равномерно распределен заряд с линейной
плотностью
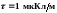 .
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
1 *.
Дано: Решение:
*.
Дано: Решение:

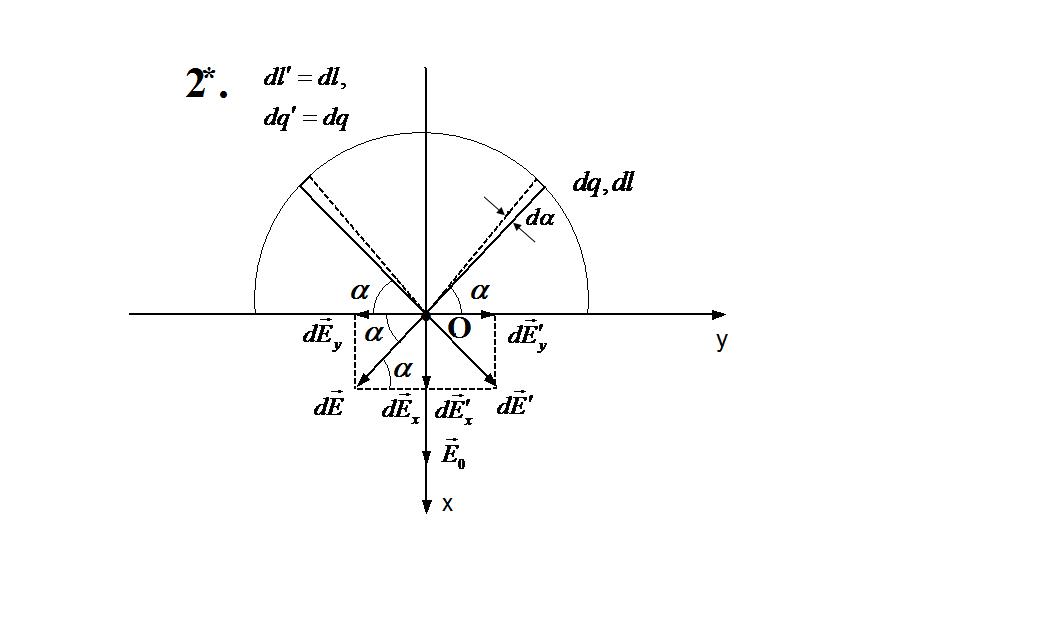
4*.
Составим полную систему уравнений для
нахождения искомой величины
 :
:
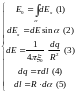
Решение
системы получается подстановкой (2),
(3), (4), (5) в (1) и интегрированием по
 в
пределах от 0 до π.
в
пределах от 0 до π.
9*.
Ответ:

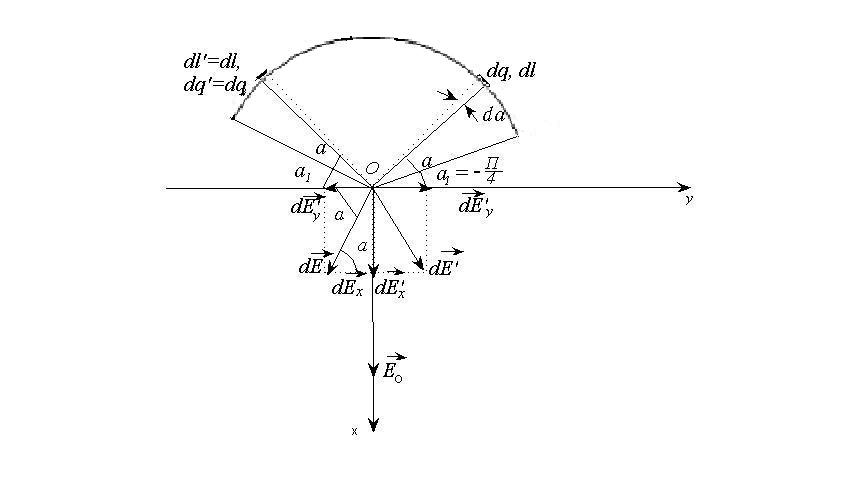
Задача 12
Треть
тонкого кольца радиуса
несет
равномерно распределенный заряд
 .
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
1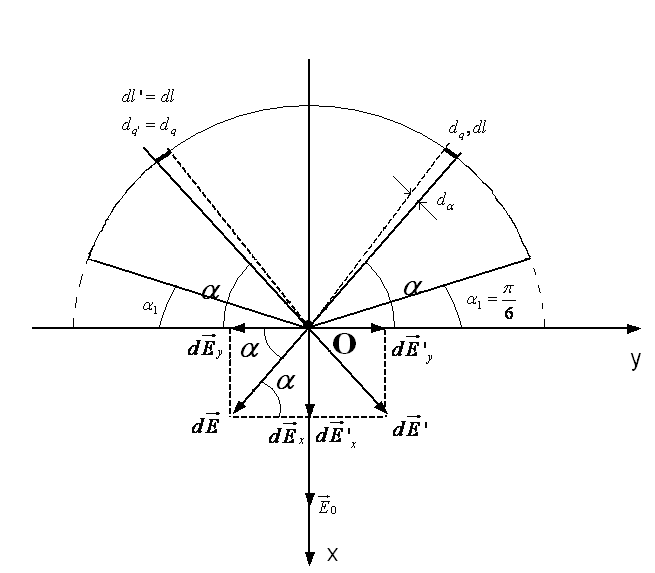 *.
Дано: Решение:
*.
Дано: Решение:
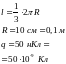
 2*.
2*.
4*. Составим полную систему уравнений для нахождения искомой величины E0:
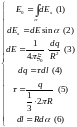
Решение
системы получается подстановкой (2),
(3), (4), (5), (6) в (1) и интегрированием по
от
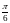 до
до
 .
.
9*. Ответ: .
Задача 13
Тонкое
кольцо несет равномерно распределенный
заряд
 .
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке А,
равноудаленной от всех точек кольца на
расстояние
.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке А,
равноудаленной от всех точек кольца на
расстояние
 .
Радиус кольца
.
.
Радиус кольца
.
1*. Дано:
|
Р 2*.
|
4*. Составим полную систему уравнений для нахождения искомой величины :

Решение
системы получается подстановкой (2),
(3), (4), (5), (6) в (1) и интегрированием по
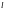 в пределах от 0 до
в пределах от 0 до
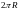 .
.
9*. Ответ:
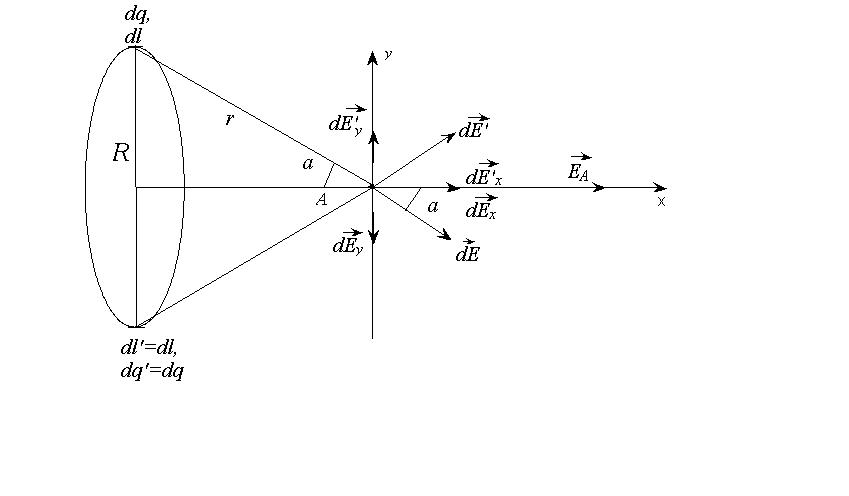
Задача 14
По
тонкому кольцу радиусом
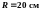 равномерно распределен с линейной
плотностью
равномерно распределен с линейной
плотностью
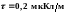 заряд.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке А,
находящейся на оси кольца на расстоянии
заряд.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке А,
находящейся на оси кольца на расстоянии
 от его центра.
от его центра.
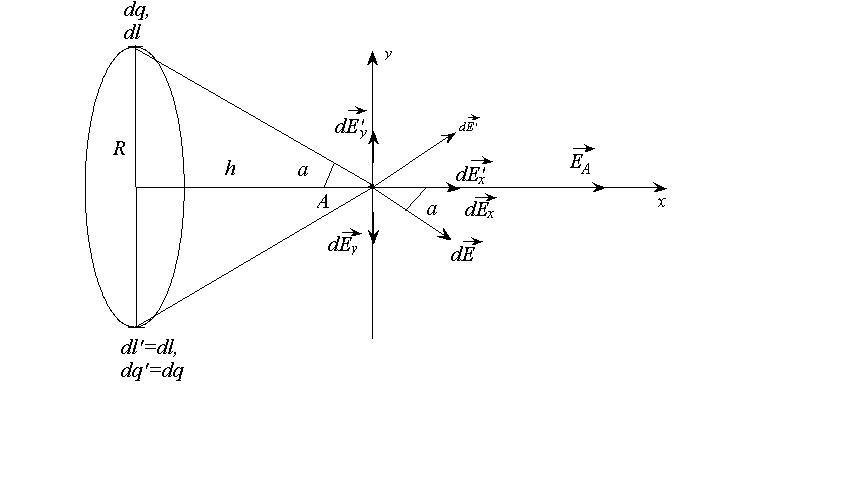
1 *. Дано:
|
Решение: 2*. |
4*. Составим полную систему уравнений для нахождения искомой величины :
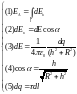
Решение системы получается подстановкой (2), (3), (4), (5), (6) в (1) и интегрированием по в пределах от 0 до .
9*. Ответ:
Задача 15
По
тонкому полукольцу равномерно распределен
заряд
 с
линейной плотностью
.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
с
линейной плотностью
.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
1*. Дано:
|
Решение: 2
|
|
|
4*. Составим полную систему уравнений для нахождения искомой величины :
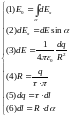
Решение
системы получается подстановкой (2),
(3), (4), (5), (6) в (1) и интегрированием по
в пределах от 0 до
 .
.
9*.
Ответ:
=
 В/м.
В/м.
Задача 16
Четверть
тонкого кольца радиуса
несет равномерно распределенный заряд
 .
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке О,
совпадающей с центром кольца.
1*. Дано:
|
Решение: 2*.
|
|
|
4*. Составим полную систему уравнений для нахождения искомой величины :

Решение
системы получается подстановкой (2),
(3), (4), (5), (6) в (1) и интегрированием по
в пределах от

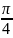 до
до
 .
.
9*. Ответ:
Задача 17
По
тонкому кольцу равномерно распределен
заряд
 с
линейной плотностью
с
линейной плотностью
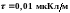 .
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке А, лежащей
на оси кольца и удаленной от его центра
на расстояние, равное радиусу кольца.
.
Определить напряженность
электрического поля, создаваемого
распределенным зарядом в точке А, лежащей
на оси кольца и удаленной от его центра
на расстояние, равное радиусу кольца.
1*. Дано:
|
Решение: 2*.
|
|
|
4*.
Составим полную систему уравнений для
нахождения искомой величины
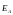 :
:
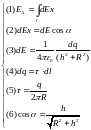
Решение системы получается подстановкой (2), (3), (4), (5), (6) в (1) и интегрированием по в пределах от 0 до .
9*.
Ответ:

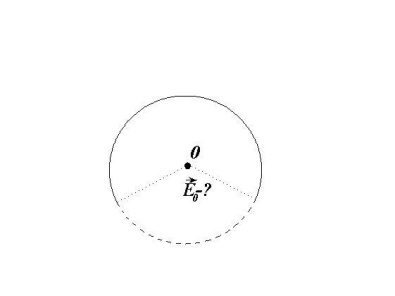
Задача 18
Две трети тонкого кольца радиусом несут равномерно распределенный с линейной плотностью заряд. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.
1 *. Дано:
|
Решение: 2*.
|
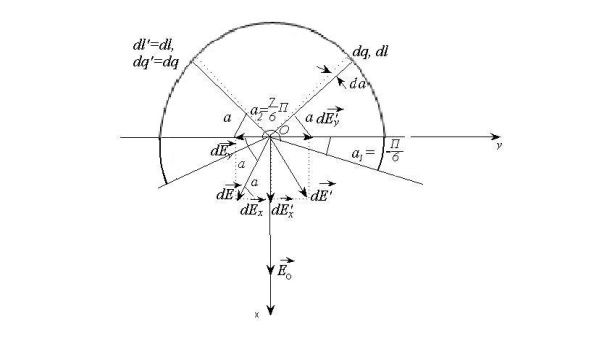
4*. Составим полную систему уравнений для нахождения искомой величины :
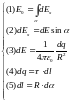
Решение
системы получается подстановкой (2),
(3), (4), (5), (6) в (1) и интегрированием по
в пределах от
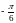 до
до
 .
.
9*.
Ответ:
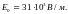
Задача 19
Два
точечных заряда
 и
и
 находятся на расстоянии
находятся на расстоянии
 друг от друга. Какую работу
друг от друга. Какую работу
 необходимо совершить внешним силам,
чтобы уменьшить расстояние между
зарядами вдвое?
необходимо совершить внешним силам,
чтобы уменьшить расстояние между
зарядами вдвое?
1*. Дано: Решение:
|
|
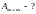
4*.
Составим полную систему уравнений для
нахождения искомой величины
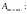

Система четырех уравнений (1) – (4) замкнута, так как содержит четыре неизвестные величины:
 Решение
системы получается подстановкой (2) ,
(3) , (4) в (1) , что приводит к единственному
уравнению с одним неизвестным.
Решение
системы получается подстановкой (2) ,
(3) , (4) в (1) , что приводит к единственному
уравнению с одним неизвестным.
9*.
Ответ:

Задача 20
Электрическое
поле создано заряженным проводящим
шаром, потенциал которого
 .
Определить работу
.
Определить работу
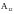 сил поля по перемещению заряда
из точки 1 в точку 2.
сил поля по перемещению заряда
из точки 1 в точку 2.
1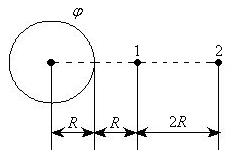 *.
Дано: 2*.
*.
Дано: 2*.
|
|
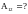
4*.
Составим полную систему уравнений для
нахождения искомой величины
 .
.
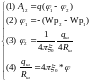
Система четырех уравнений (1) – (4) замкнута, так как содержат четыре неизвестные величины:
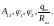
Решение системы получается подстановкой (2) , (3) , (4) в (1) , что приводит к единственному уравнению с одним неизвестным.
9*.
Ответ:

Задача 21
Электрическое
поле создано зарядами
 и
и
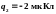 ,
находящимися на расстоянии
друг от друга. Определить работу
,
находящимися на расстоянии
друг от друга. Определить работу
 сил поля, совершаемую при перемещении
заряда
сил поля, совершаемую при перемещении
заряда
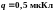 из точки 1 в точку 2.
из точки 1 в точку 2.
1*. Дано: Решение:
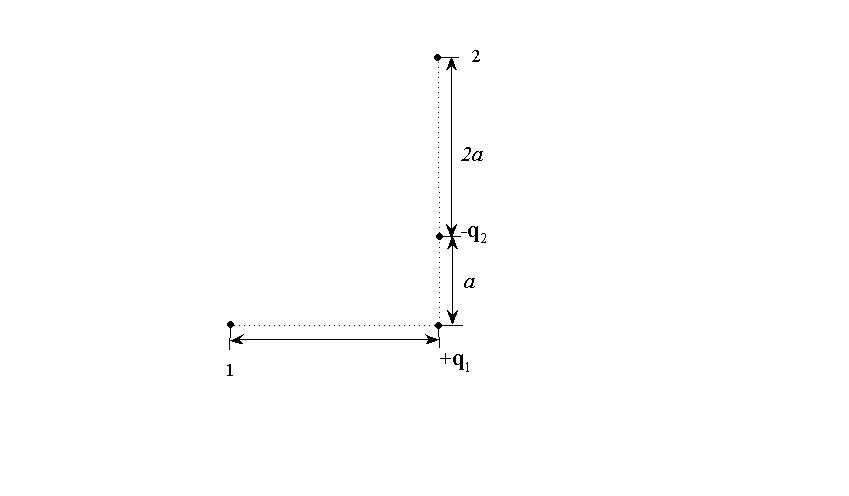
 2*.
2*.

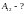
4*. Составим полную систему уравнений для нахождения искомой величины :

Полученная
система уравнений (1)-(7) замкнута, так
как содержит семь неизвестных величин
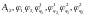 .
.
9*.
Ответ:
 .
.
Задача 22
Тонкий
стержень согнут в кольцо радиусом
.
Он равномерно заряжен с линейной
плотностью заряда
 .
Определить
потенциал
.
Определить
потенциал
 электрического поля в точке, находящейся
на оси кольца на расстоянии
электрического поля в точке, находящейся
на оси кольца на расстоянии
 от его центра.
от его центра.
1*. Дано: Решение:
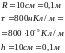
 2*.
2*.

4*.
Составим полную
систему уравнений
для нахождения искомой величины
 :
:

Решение
системы (1)-(4) получается подстановкой
(2),(3),(4) в (1) и интегрированием по
в пределах от
 до
.
до
.
9*.
Ответ:
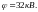
Задача 23
Электрическое
поле образовано бесконечно длинной
заряженной нитью, линейная плотность
заряда которой
 .
Определить разность потенциалов
.
Определить разность потенциалов
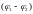 между двумя точками поля, отстоящих от
нити на расстоянии
между двумя точками поля, отстоящих от
нити на расстоянии
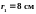 и
и
 .
.
1*. Дано Решение:
|
2*. |

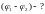
4*. Составим полную систему уравнений для нахождения искомой величины :

Решение
системы (1) – (3) получается подстановкой
(1) и (2) в (3) и интегрированием по r в
пределах от .
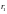 до
до .
.
9*.
Ответ:
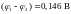
Задача 24
Пылинка
массой
 ,
несущая на себе заряд
,
несущая на себе заряд
 ,
влетела в электрическое поле в направлении
силовых линий. После прохождения разности
потенциалов
,
влетела в электрическое поле в направлении
силовых линий. После прохождения разности
потенциалов
 пылинка имела скорость
пылинка имела скорость
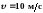 .
Определить скорость
.
Определить скорость
 пылинки до того, как она влетела в поле.
пылинки до того, как она влетела в поле.
1*. Дано Решение:
|
2*. |

4*.
Составим полную систему уравнений для
нахождения искомой величины
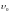 :
:
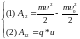
Полученная
система уравнений (1) – (2) замкнута, так
как содержит две неизвестные величины
 .
.
9*.
Ответ:
 .
.
Задача 25
Электрон,
обладавший кинетической энергией
 ,
влетел в однородное электрическое поле
в направлении силовых линий. Какой
скоростью будет обладать электрон,
пройдя в этом поле разность потенциалов
,
влетел в однородное электрическое поле
в направлении силовых линий. Какой
скоростью будет обладать электрон,
пройдя в этом поле разность потенциалов
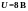 ?
?
1 *. Дано: СИ: Решение:
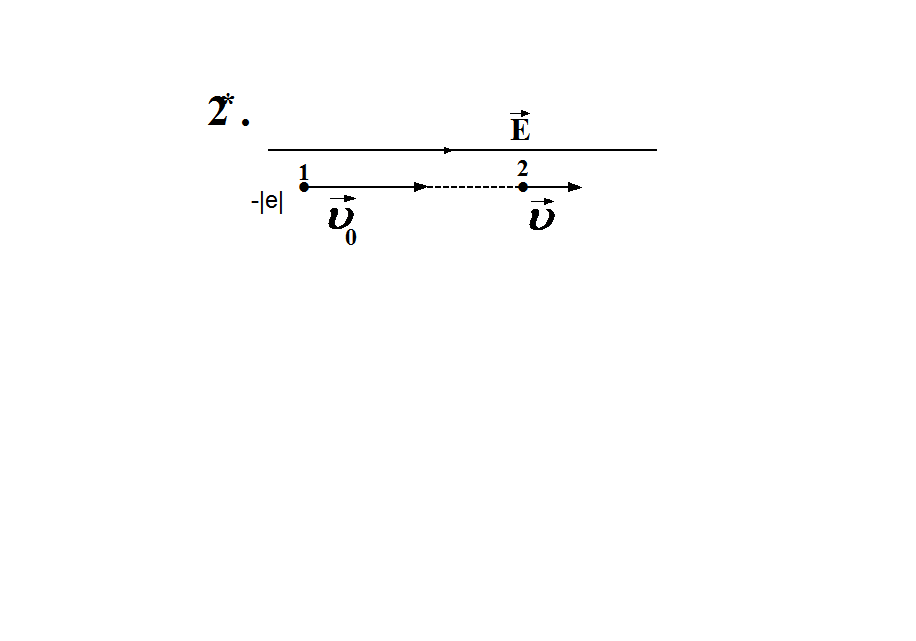

 -?
-?
4*.
Составим полную систему уравнений для
нахождения искомой величины
 :
:

Полученная
система уравнений
 замкнута, так как содержит две неизвестные
величины
замкнута, так как содержит две неизвестные
величины
 ,
,
 .
.
9*.
Ответ:

Задача 26
Электрон,
пройдя в плоском конденсаторе путь от
одной пластины до другой, приобрел
скорость
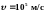 .
Расстояние между пластинами
.
Расстояние между пластинами
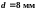 .
Найти: 1) разность потенциалов
.
Найти: 1) разность потенциалов
 между пластинами; 2) поверхностную
плотность заряда
между пластинами; 2) поверхностную
плотность заряда
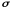 на
пластинах.
на
пластинах.
1 *. Дано: СИ: Решение:
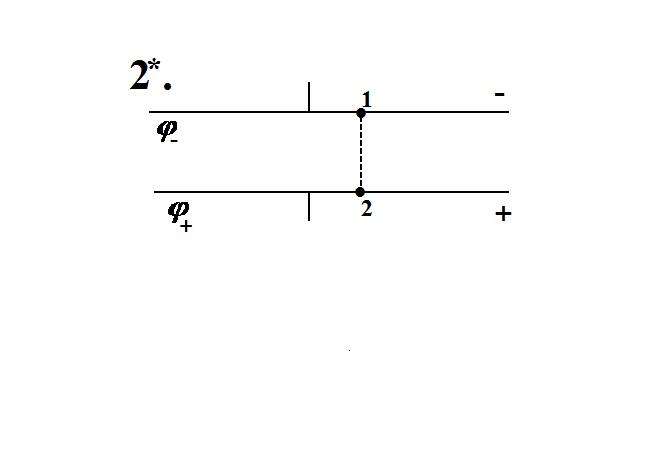


1) -?
2) -?
4*. 1) Составим полную систему уравнений для нахождения искомой величины :

Полученная
система (1)-(3) замкнута, так как содержит
три неизвестные величины
, ,
.
,
.
2) Составим полную систему уравнений для нахождения искомой величины :

Полученная
система уравнений (1)-(5) замкнута, так
как содержит пять неизвестных величин:
,
 ,
,
,
.
,
,
,
.
9*.
Ответ:
1)
 ;
2)
;
2)
 .
.
Задача 27
Пылинка
массой
 ,
несущая на себе
,
несущая на себе
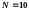 электронов,
прошла в вакууме ускоряющую разность
потенциалов
электронов,
прошла в вакууме ускоряющую разность
потенциалов
 .
Какова кинетическая энергия
.
Какова кинетическая энергия
 пылинки. Какую скорость
пылинки. Какую скорость
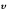 приобрела пылинка? 1*.
Дано:
Решение:
приобрела пылинка? 1*.
Дано:
Решение:
|
|


4*. 1) Составим полную систему уравнений для нахождения искомой величины :
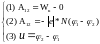
Полученная
система уравнений (1) – (3) замкнута, так
как содержит три неизвестные величины
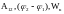
Составим
полную систему уравнений для нахождения
искомой величины
 :
:

Полученная
система уравнений (1) – (4) замкнута, так
как содержит четыре неизвестные величины
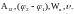
9*.
Ответ: 1)
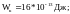 2)
2)
 .
.
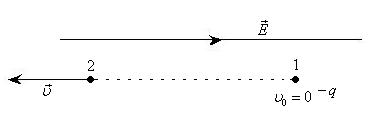
Задача 28
В
однородное электрическое поле
напряженностью
 влетает
(вдоль силовой линии) электрон со
скоростью
влетает
(вдоль силовой линии) электрон со
скоростью
 .
Определить расстояние
.
Определить расстояние
 ,
которое пройдет электрон до точки, в
которой его скорость будет равна половине
начальной.
,
которое пройдет электрон до точки, в
которой его скорость будет равна половине
начальной.
1*. Дано 2*. Решение:
|
|
 4*.
Составим полную систему уравнений для
нахождения искомой величины
4*.
Составим полную систему уравнений для
нахождения искомой величины

Полученная
система уравнений (1) – (3) замкнута, так
как содержит три неизвестные величины:
9*.
Ответ:

Задача 29
Электрическое
поле создано бесконечной заряженной
прямой линией с равномерно распределенным
зарядом
 .
Определить кинетическую энергию
.
Определить кинетическую энергию
 электрона в точке 2, если в точке 1 его
кинетическая энергия
электрона в точке 2, если в точке 1 его
кинетическая энергия
 .
.
1*. Дано: Решение:
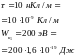

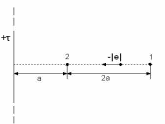 2*
2*
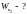
4*. Составим полную систему уравнений для нахождения искомой величин Wк2:
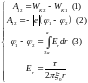
Полученная
система уравнений (1)-(4) замкнута, так
как содержит четыре независимые величины

Ответ:
 .
.
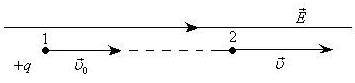
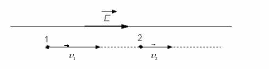
Задача 30
Электрон
движется вдоль силовой линии однородного
электрического поля. В некоторой точке
поля с потенциалом
 электрон имел скорость
электрон имел скорость
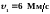 .
Определить потенциал
.
Определить потенциал
 точки поля, дойдя до которой электрон
потеряет половину своей скорости.
точки поля, дойдя до которой электрон
потеряет половину своей скорости.
1 *.
Дано: Решение:
*.
Дано: Решение:

 2*.
2*.

4*. Составим полную систему уравнений для нахождения искомой величины φ2:

Полученная
система уравнений (1)-(3) замкнута, так
как содержит три неизвестные величины:
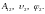




 ешение:
ешение:

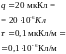 =
=


 *.
*.