3.4. Потери напора

Движущийся поток жидкости на своем пути преодолевает силы трения жидкости о стенки трубы или канала и различные местные сопротивления, вследствие чего возникают потери удельной энергии. Потери напора различают двух видов:

- потери по длине потока h_l;

- потери на преодоление местных сопротивлений h_м.с..

Полные потери напора равны сумме всех потерь

. (29)

3.4.1. Потери напора по длине

При равномерном движении в трубах потери напора по длине, как при турбулентном, так и при ламинарном движении определяются для круглых труб по формуле Дарси:

, (30)

а для труб любой другой формы сечения по формуле:

. (31)

В некоторых случаях также используют формулу:

. (32)

Потери давления на трение по длине , Па, определяются по формуле:

, (33)

где		- соответственно длина участка трубы или канала, м;
		- диаметр эквивалентный, м;
		- средняя скорость течения, м/с;
		- гидравлический радиус трубы, м.
		- коэффициент гидравлического трения;
	С	- коэффициент Шези, связанный с коэффициентом гидравлического трения зависимостями:

; .

В зависимости от режима движения применяются различные формулы для определения коэффициента гидравлического трения.

Ламинарный режим.

При движении жидкости по трубам круглого сечения:

, (34)

а для труб любой формы сечения:

, (35)

где А - коэффициент, численное значение которого зависит от формы поперечного сечения трубы.

Тогда формула для определения потерь напора по длине при ламинарном режиме принимает вид:

. (36)

Турбулентный режим.

При турбулентном движении различают три области гидравлических сопротивлений:

1. область гидравлически гладких труб при числе Рейнольдса ( - эквивалентная шероховатость);

, (37)

или

. (38)

2. переходная область сопротивлений при

. (39)

3. автомодельная область (или квадратичная область сопротивления) при

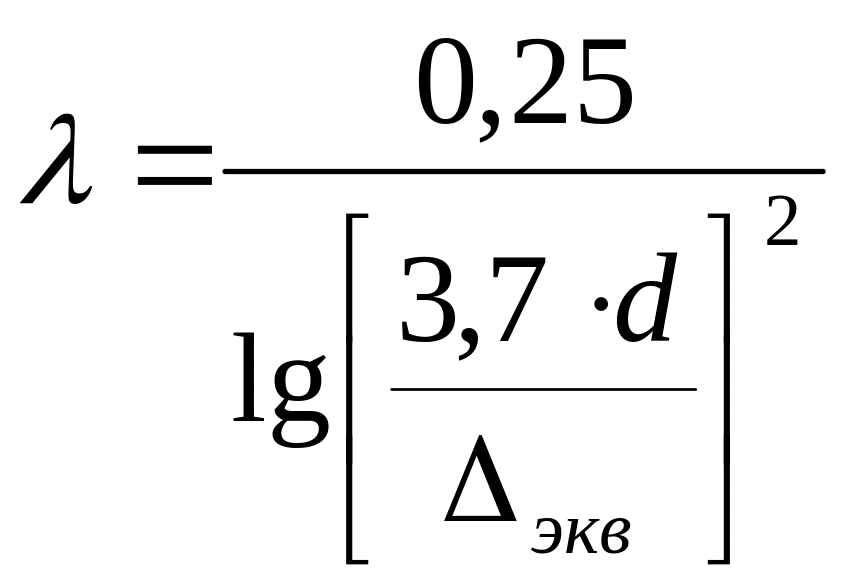, (40)

или

. (41)

3.4.2. Потери напора на местные сопротивления

Местные потери h_м.с возникают в местах, где изменяется конфигурация потока, приводящая к деформации эпюр распределения скоростей и зависят от скорости течения и вида местных сопротивлений. Движение в трубопроводе при наличии местных сопротивлений является неравномерным. Определяются по эмпирической формуле Вейсбаха:

, (42)

где - коэффициент гидравлических сопротивлений для местных потерь напора.

Значения коэффициентов местных сопротивлений зависят от конфигурации местного сопротивления и режима потока, подходящего к сопротивлению.

1. Внезапное расширение потока.

Потери напора при внезапном расширении (рис. 7) трубопровода находят по формуле Борда:

, (43)

где - средние скорости течения соответственно до и после расширения, м/с.

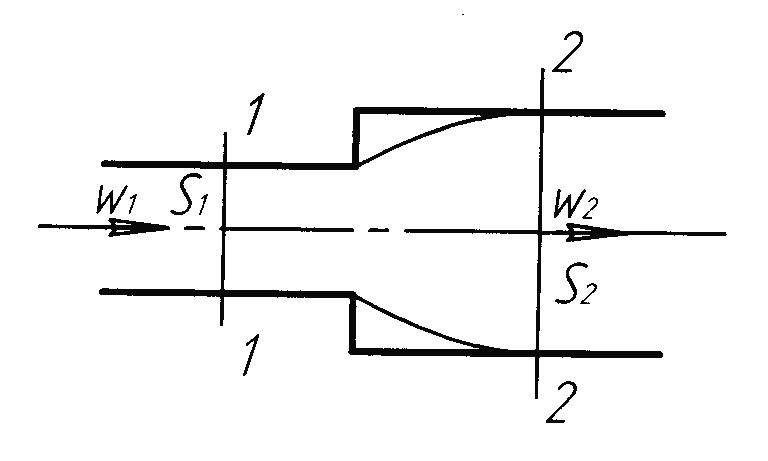
Рис. 7. Внезапное расширение трубопровода

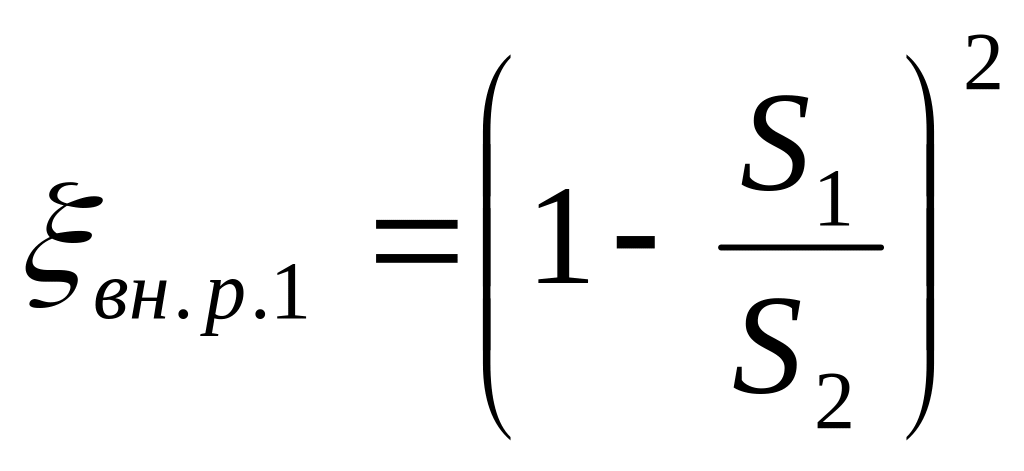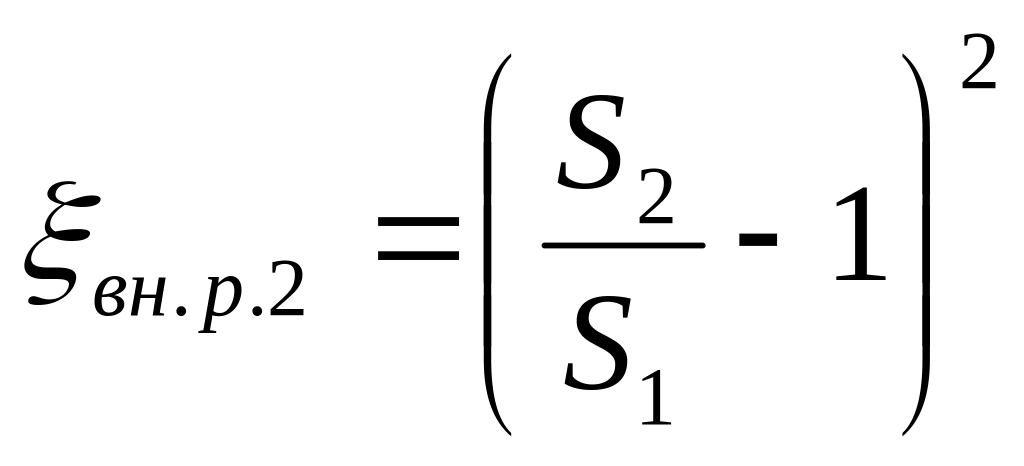; , (44)

где , - площадь поперечного сечения трубопровода до и после расширения соответственно, м².

Значения приведены в приложении 7.

2. Внезапное сужение трубопровода.

Коэффициент местного сопротивления при внезапном сужении (рис. 8):

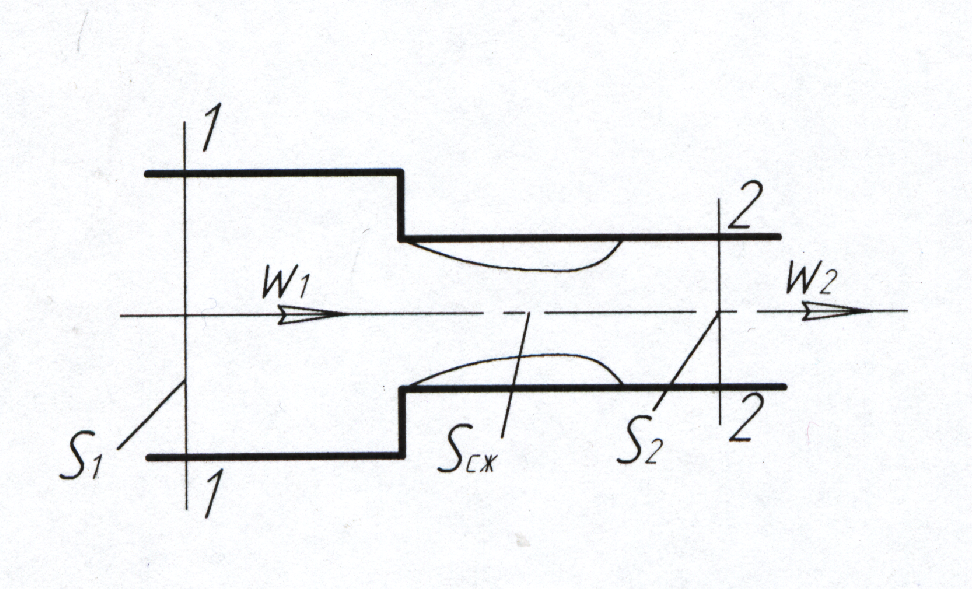
Рис. 8. Внезапное сужение трубопровода

, (45)

где - коэффициент сжатия струи, представляющий собой отношение площади сечения сжатой струи в узком трубопроводе к площади сечения узкой трубы

. (46)

Коэффициент сжатия струи зависит от степени сжатия потока

, (47)

и может быть найден по формуле Альтшуля:

. (48)

Значения , подсчитанные по формуле (48) приведены в табл. 1.

Таблица 1

п	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
	0,609	0,613	0,618	0,623	0,631	0,642	0,656	0,678	0,713	0,785	1

Значения приведены в приложении 8.

3. Диафрагма на трубопроводе.

Коэффициент местного сопротивления диафрагмы (рис. 9), расположенной внутри трубы постоянного сечения (отнесенный к сечению трубопровода):

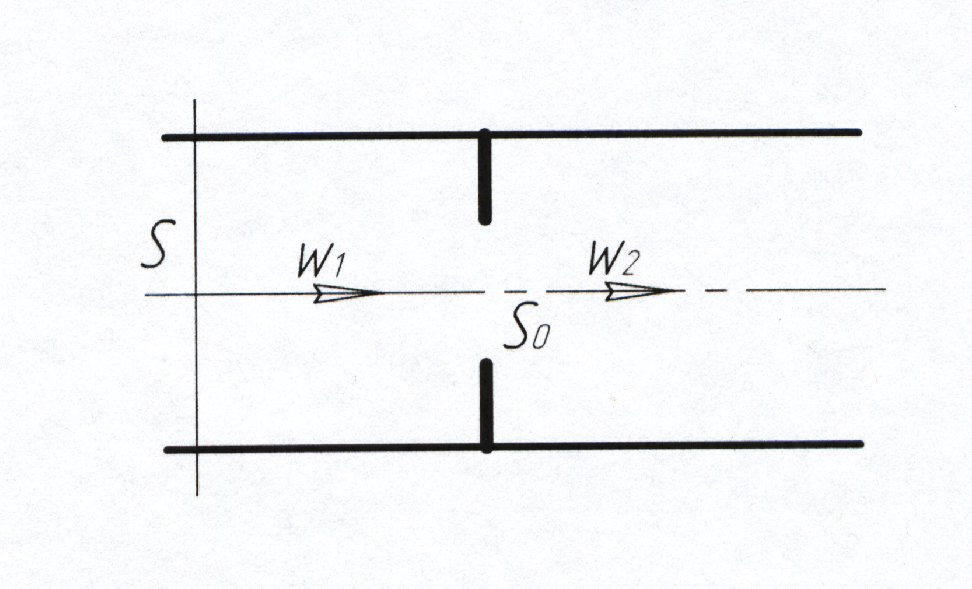
Рис. 9. Диафрагма на трубопроводе

, (49)

где - отношение площади отверстия диафрагмы к площади сечения трубы.

Значения приведены в приложении 9.

4. Вход в трубу из резервуара.

Для коэффициента сопротивления следует принимать следующие значения:

- при острых кромках	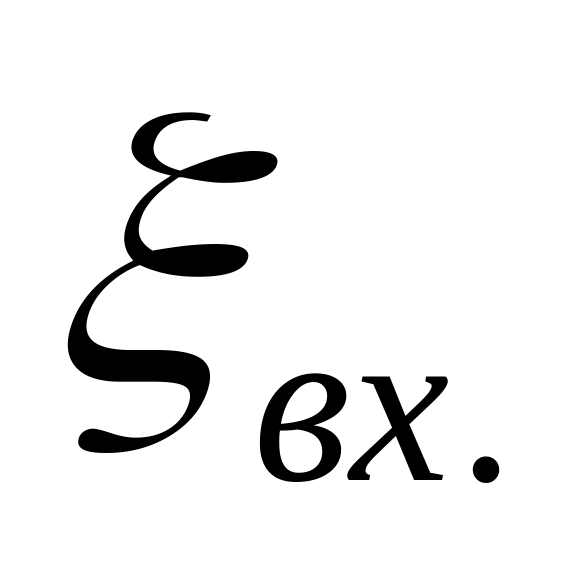= 0,4 - 0,5;
- при закругленных кромках	= 0,2;
- при плавном входе	= 0,05.

5. Выход из трубы в резервуар.

Коэффициент сопротивления , отнесенный к сечению трубы:

. (50)

При выходе из трубы через диафрагму в конце трубопровода (рис. 10)

. (51)

Значения приведены в приложении 10.

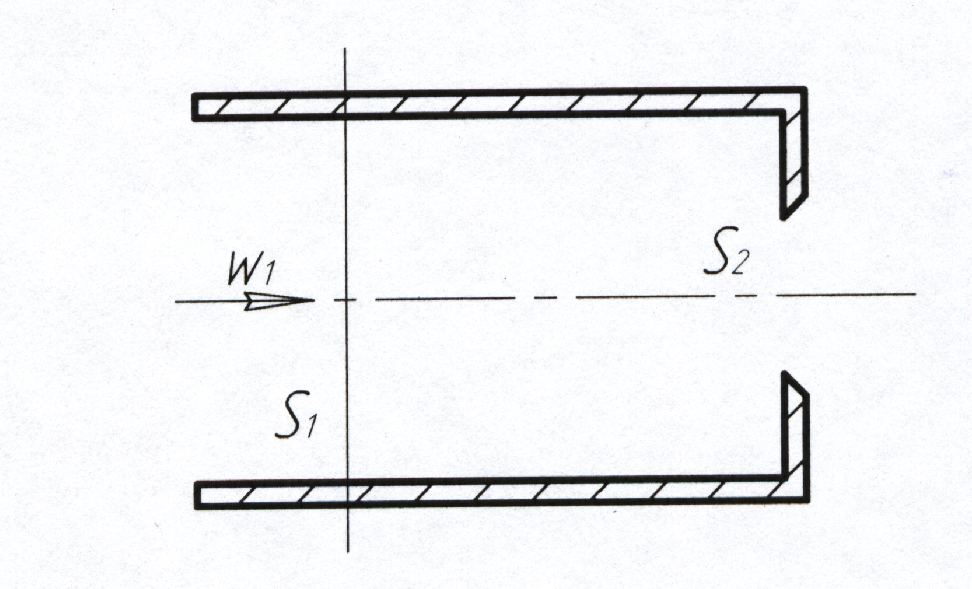
Рис. 10. Вход из трубы через диафрагму

6. Постепенное расширение трубопровода.

Коэффициент сопротивления для конически расходящихся переходных конусов (диффузоров) зависит от угла конусности и соотношения диаметров (рис. 11). Для коротких конусов коэффициент сопротивления, отнесенный к более широкому сечению:

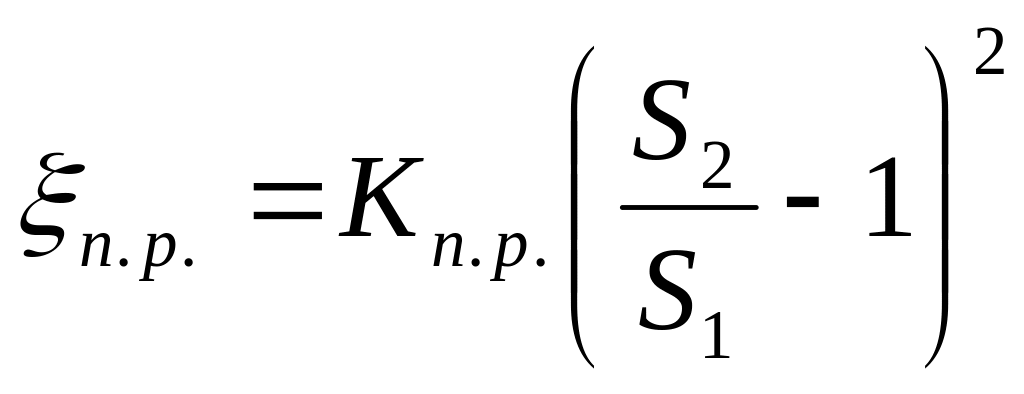, (52)

где - коэффициент смягчения при постепенном расширении, зависящий от угла конусности α (рис. 11), значения приведены в табл. 2.

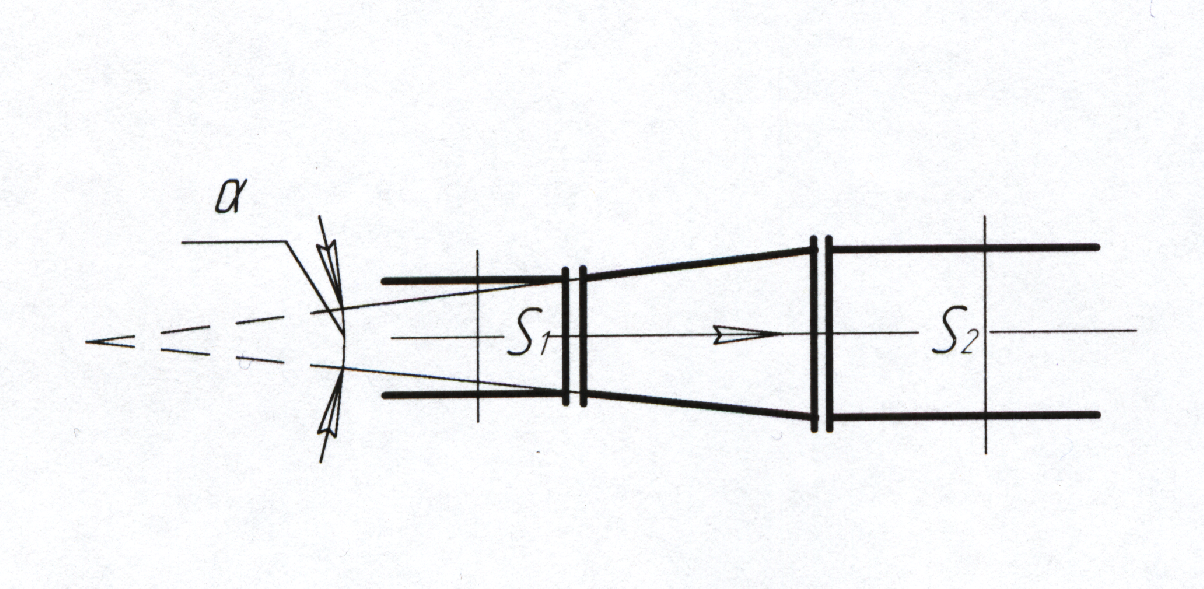
Рис. 11. Постепенное расширение трубопровода

Таблица 2

α, град	4	8	15	30	60	90
	0,08	0,16	0,65	0,80	0,95	1,07

Для длинных конусов нужно учитывать также потери по длине.

7. Постепенное сужение трубопровода.

Коэффициент сопротивления для сходящихся переходных конусов (конфузоров) зависит от угла конусности и соотношения диаметров. Для коротких конусов:

, (53)

где - коэффициент смягчения при постепенном сужении, зависящий от угла конусности α, значения приведены в табл. 3.

Таблица 3

α, град	10	20	40	60	80	100	140
	0,40	0,25	0,20	0,20	0,30	0,40	0,60

8. Потери напора при повороте трубы.

а) Резкий поворот трубы круглого поперечного сечения на угол α.

, (54)

где - значение коэффициента сопротивления для угла 90⁰ (приложение 11); для ориентировочных расчетов следует принимать .

б) плавный поворот трубы круглого поперечного сечения (закругленное колено, отвод, рис. 12).

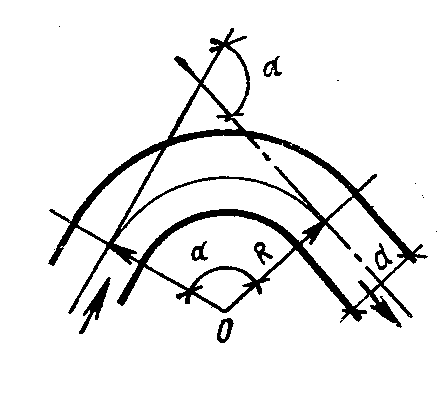
Рис. 12. Плавный поворот трубы

, (55)

Значение параметра приведены в приложении 12.

Коэффициент определяется по формуле Альтшуля:

, (56)

где d – диаметр трубопровода, м;

R – радиус закругления, м.

9. Потери напора в запорных устройствах.

Значения коэффициентов местных сопротивлений для некоторых запорных устройств (задвижка, вентиль, кран и др.) приведены в приложении 11.

Теоретические значения коэффициента сопротивления для задвижки можно также найти по формуле:

, (57)

где S – площадь сечения, не стесненная запорным устройством, м²;

S₀ – площадь сечения трубы, м².

10. Потери напора в сетках.

Для сеток с квадратными ячейками коэффициент сопротивления:

, (58)

где		- коэффициент скважности сетки (а – размер стороны ячейки сетки; t – шаг сетки, м);
		- средняя скорость в ячейках сетки , здесь - средняя скорость на подходе к сетке, м/с.