9.2.2.3 Режим смешанных волн

В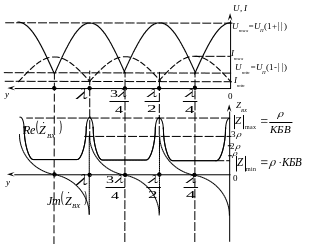 РСМВ за счет частичного поглощения энергии нагрузкой амплитуда отраженной волны меньше амплитуды падающей. Следовательно, даже в точках, где суммируются волны в противофазе не может быть полной компенсации и вместо узлов образуются минимумы. Соответственно, при суммировании падающей и отраженной волн, находящихся в фазе, образуются не пучности, а максимумы (рисунок 9.4).

Рисунок 9.4 - Зависимости U(y y _ВХy для R_Н

Значения токов, напряжений и Z_ВХ в конце линии определяются конкретными значениями нагрузок (при фиксированных значениях , _В, _i).

Мгновенные значения напряжений в РСМВ:

(9.8)

Первое слагаемое выражения (9.8) описывает бегущую волну, второе - стоячую. Соотношение доли бегущей и стоячей волн принято оценивать коэффициентом бегущей волны (КБВ) или обратным ему коэффициентом стоячей волны (КСВ)

КБВ = КСВ = . (9.9)

9.2.2.4 Работа лбп при изменяющейся чисто активной нагрузке

Весьма наглядно режимы работы ЛБП проявляются при изменении чисто активной нагрузки в пределах 0 - .

Таблица 9.2 - Распределение амплитуд напряжений вдоль линии

для разных активных нагрузок

Режим	U(y	Нагрузка		Р
РСВ		RН = 0 к.з.	1	1800
РСМВ		RН  	менее 1	1800
РБВ		RН = 	0	00
РСМВ		RН  	менее 1	00
РСВ		RН =  х.х.	1	00

9.2.3 Линия с потерями

Распределение токов и напряжений в линии с потерями в общем случае определяется выражениями (9.1) и (9.2), а входное сопротивление выражением (9.3). Наиболее наглядно влияние потерь можно оценить на примере РСВ.

В РСВ, независимо от наличия потерь, в конце линии, где х =  или y = 0,

или

Однако, по мере удаления от конца к началу линии значения напряжения в узлах и пучностях в линии с потерями все сильнее отличаются от идеальных. Так при встрече в противофазе падающей и отраженной волн (см. рисунок 9.2) уже не происходит их полного поглощения ( ), а образуется остаток или минимум, который тем больше, чем ближе к началу линии.

В “бывших узлах”

(9.10)

соответственно в “бывших пучностях” U_max(y) уже не равен 2 а имеет выражение

. (9.11)

Входные сопротивления ЛБП в РСВ имеют реактивный характер, а по модулю представляют чередование нулевых и бесконечно больших значений как на рисунке 9.5.а. Из-за потерь входное сопротивление становится комплексным, значения в “бывших нулях”

, при y<<1 ; (9.12)

в “бывших бесконечностях”

, при y<<1 , (9.13)

где  определяется погонными параметрами.

При y   Z_ВХ(y)  Z_В, как показано на рисунке 9.5.б для короткозамкнутой линии.

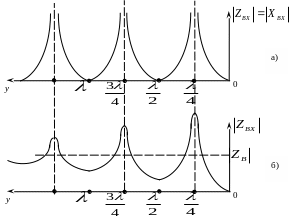
Рисунок 9.5 - Модуль входного сопротивления ЛБП (а) и линии

с потерями (б) при Z_Н=0 (к.з.)