Примеры
Пример
7.1. Определить
плотность вероятности величины
,
если X
- случайная величина, равномерно
распределенная на интервале
.
Решение.1.
Построим график величины
для x
в интервале
и определим диапазон значений Y:
(рис. 7.1).
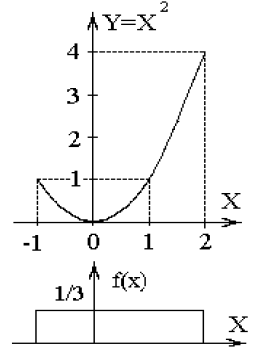
Рис. 7.1
2. В зависимости от числа k обратных функций выделим следующие интервалы для Y:
3.
На интервалах
и
обратные
функции не существует.
В
интервале
две обратных функции:
и
.
Вычислим модули производных обратных функций :
В
интервале
одна обратная функция
,
следовательно,
.
4. Так как Х равномерно распределена в интервале -1, 2, то ее плотность вероятности равна
По формуле (7.1) получим плотность вероятности величины Y
Задача 8. Двухмерные случайные величины Условия вариантов задачи
В задачах 8.1-8.40 (конкретные параметры приведены в табл. 8.1) двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 8.1 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
Вычислить коэффициент корреляции между величинами X и Y.
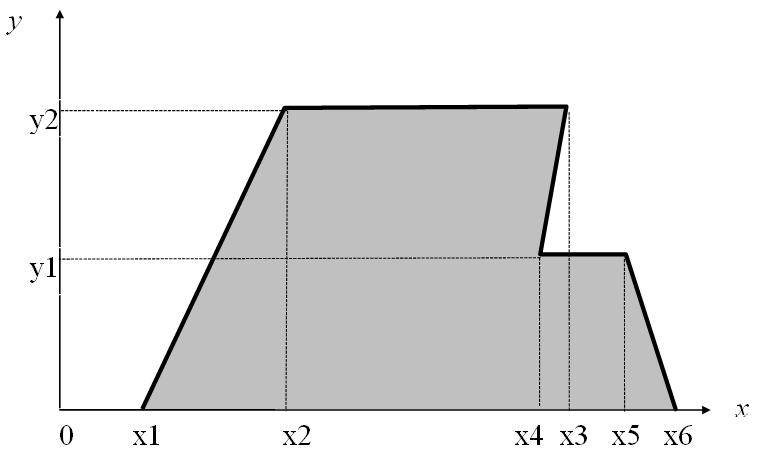
Рис. 8.1
Т
Вариант |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
y1 |
y2 |
8.1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
2 |
8.2 |
0 |
2 |
2 |
2 |
2 |
2 |
1 |
2 |
8.3 |
0 |
0 |
0 |
2 |
2 |
4 |
1 |
2 |
8.4 |
0 |
2 |
4 |
4 |
4 |
4 |
1 |
2 |
8.5 |
0 |
0 |
2 |
3 |
3 |
4 |
1 |
2 |
8.6 |
0 |
0 |
6 |
6 |
6 |
6 |
1 |
2 |
8.7 |
2 |
0 |
4 |
5 |
5 |
6 |
1 |
2 |
8.8 |
0 |
0 |
2 |
2 |
4 |
4 |
1 |
2 |
8.9 |
0 |
0 |
4 |
2 |
2 |
0 |
1 |
2 |
8.10 |
0 |
0 |
4 |
4 |
2 |
2 |
1 |
2 |
8.11 |
0 |
2 |
2 |
3 |
3 |
4 |
1 |
2 |
8.12 |
0 |
1 |
4 |
5.5 |
5.5 |
6 |
1 |
2 |
8.13 |
0 |
2 |
2 |
4 |
4 |
6 |
1 |
2 |
8.14 |
0 |
4 |
4 |
5 |
5 |
6 |
1 |
2 |
8.15 |
4 |
0 |
8 |
10 |
10 |
12 |
1 |
2 |
8.16 |
0 |
0 |
4 |
5 |
5 |
6 |
1 |
2 |
8.17 |
0 |
0 |
4 |
4 |
4 |
4 |
1 |
2 |
8.18 |
0 |
3 |
3 |
3 |
3 |
3 |
1 |
2 |
8.19 |
0 |
0 |
0 |
2 |
2 |
4 |
1 |
2 |
8.20 |
0 |
2 |
6 |
6 |
6 |
6 |
1 |
2 |
8.21 |
3 |
0 |
5 |
6,5 |
6,5 |
8 |
1 |
2 |
8.22 |
0 |
0 |
4 |
4 |
4 |
6 |
1 |
2 |
8.23 |
0 |
0 |
4 |
2 |
2 |
0 |
1 |
2 |
8.24 |
0 |
0 |
5 |
5 |
5 |
5 |
1 |
2 |
8.25 |
0 |
4 |
4 |
6 |
6 |
8 |
1 |
2 |
8.26 |
0 |
4 |
6 |
7 |
7 |
8 |
1 |
2 |
8.27 |
1 |
0 |
3 |
2,5 |
2,5 |
4 |
1 |
2 |
8.28 |
0 |
2 |
4 |
4 |
6 |
6 |
1 |
2 |
8.29 |
0 |
2 |
4 |
4 |
5 |
6 |
1 |
2 |
8.30 |
0 |
1 |
3 |
5 |
5 |
7 |
1 |
2 |
8.31 |
0 |
0 |
0 |
1 |
1 |
2 |
1 |
2 |
8.32 |
0 |
2 |
6 |
5 |
5 |
4 |
1 |
2 |
8.33 |
0 |
0 |
2 |
1 |
1 |
0 |
1 |
2 |
8.34 |
0 |
2 |
4 |
5 |
5 |
6 |
1 |
2 |
8.35 |
0 |
2 |
4 |
2 |
2 |
0 |
1 |
2 |
8.36 |
0 |
4 |
4 |
4 |
4 |
4 |
1 |
2 |
8.37 |
0 |
0 |
2 |
4 |
4 |
6 |
1 |
2 |
8.38 |
0 |
0 |
6 |
6 |
4 |
4 |
1 |
2 |
8.39 |
0 |
2 |
4 |
6 |
6 |
8 |
1 |
2 |
8.40 |
0 |
2 |
4 |
5 |
6 |
7 |
1 |
2 |