
Завдання
На основі абстрактних статистичних даних про залежність Х та У:
Оцінити параметри економетричної моделі парної лінійної регресії за допомогою МНК, використовуючи систему рівнянь і матричний оператор В;
Дати загальну характеристику адекватності моделі та її параметрів для рівня значущості α = 0,05:
обчислити залишкову дисперсію σu2 та стандартну похибку S;
перевірити тісноту загального впливу незалежної змінної на залежну змінну, обчисливши коефіцієнт детермінації R2 ;
перевірити на значущість коефіцієнтів регресії за допомогою F- і t- статистик;
перевірити на значущість вибіркового коефіцієнта кореляції
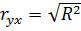 за допомогою t
– статистики;
за допомогою t
– статистики;визначити і записати межі надійності для R;
знайти надійні інтервали для регресії ;
визначити інтервали довіри для параметрів регресії.
Розрахувати точковий та інтервальний прогноз прибутку фірми для заданого прогнозного значення інвестицій: Хпр=7.
Розв’язання
Нехай задана таблиця статистичних експериментальних даних досліджуваної залежності :Уі , Хі, і = 1, n
За нашою умовою ми будемо мати наступні дані, які наведені у таблиці:
№ |
Уі |
Хі |
1 |
7,7 |
1 |
2 |
11,3 |
2 |
3 |
18,7 |
3 |
4 |
23,3 |
4 |
5 |
27,7 |
5 |
6 |
29,3 |
6 |
1. Для оцінки параметрів регресивної моделі використовуємо функцію в Excel «ЛИНЕЙН».
Ця функція має вигляд ЛИНЕЙН ( відомі значення значення у; відомі значення х; конст; статистика). Ця функція застосовує метод найменших квадратів.
«Відомі значення у» - множина значень у. «Відомі значення х» - множина значень х, що враховує або одну ( парна регресія), або кілька змінних (множинна регресія).
«Конст» - логічне значення. «Статистика» - логічне значення, яке вказує, чи потрібно обчислювати додаткову статистику за регресією. Якщо статистика має значення «ИСТИНА» або 1, то функція ЛИНЕЙН обчислює додаткову регресійну статистику у вигляді масиву.
Виділимо діапазон клітинок розміром 5×2 та у строчці формул отримаємо функцію «=ЛИНЕЙН(В2:В7,С2:С7,1,1)».
Тоді отримаємо:
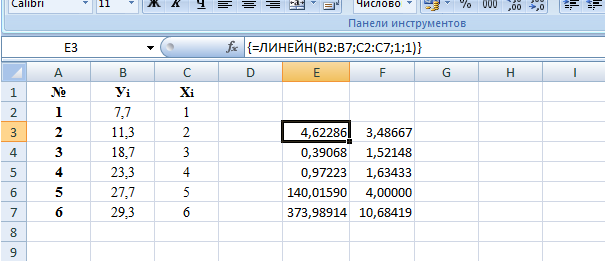
Після введення функції натискаємо F2 а потім комбінацію клавіш Ctrl+Shift+Enter. У масиві розміром 5×2 отримаємо необхідну статистику за регресією.
4,62286 |
3,48667 |
0,39068 |
1,52148 |
0,97223 |
1,63433 |
140,01590 |
4,00000 |
373,98914 |
10,68419 |
Де перший рядок містить значення параметрів парного лінійного рівняння регресії,тобто:
Відповідна 4,62286– оцінка параметра b1 ; 3,48667– оцінка параметра b0.
В другому рядку міститься значення стандартних похибок оцінок відповідних параметрів парного лінійного рівняння регресії: для параметра b0 він дорівнює 0,39068, а для параметра b1 він дорівнює 1,52148.
В першій комірці третього рядка знаходиться значення коефіцієнта детермінації R2, який дорівнює 0,97223; а друга комірка містить значення стандартної похибки залишків 1,63433.
В першій комірці четвертого рядка містить фактичне значення F-критерію, яке в нашому прикладі становить 140,01590; а друга комірка містить число ступенів свободи (n – m – 1), де n – кількість спостережень, m – кількість змінних у моделі: у нашому випадку n = 6, m = 1; це значення необхідне для визначення табличного значення F-критерію.
В
першій
комірці п'ятого рядка знаходиться
величина суми квадратів відхилень
значень результативної ознаки, обчислену
за парним лінійним рівнянням регресії,
від середнього її значення, обчисленого
за фактичними значеннями Σ
(![]() і
– Y
)2=
373,98914,
а друга комірка містить значення суми
квадратів відхилень фактичних значень
результативної ознаки від її значень,
обчислених за рівнянням регресії
Σ (Yі
-
і)2
=10,68419.
і
– Y
)2=
373,98914,
а друга комірка містить значення суми
квадратів відхилень фактичних значень
результативної ознаки від її значень,
обчислених за рівнянням регресії
Σ (Yі
-
і)2
=10,68419.
Параметри регресії будуть такими:
b1=4,62286;
b0= 3,48667.
Таким чином вибіркова регресійна функція записується у такому вигляді:
![]() =3,48667+
4,62286
*х.
=3,48667+
4,62286
*х.
Побудуємо рівняння парної регресії використовуючи систему рівнянь. Побудуємо додаткову таблицю у вигляді:
Таблиця 1:
№ |
Уі |
Хі |
Хі2 |
Хі*Уі |
1 |
7,7 |
1 |
1 |
7,7 |
2 |
11,3 |
2 |
4 |
22,6 |
3 |
18,7 |
3 |
9 |
56,1 |
4 |
23,3 |
4 |
16 |
93,2 |
5 |
27,7 |
5 |
25 |
138,5 |
6 |
29,3 |
6 |
36 |
175,8 |
Σ |
118 |
21 |
91 |
493,9 |
Підставимо, отримані в таблиці значення в систему вигляду (1):
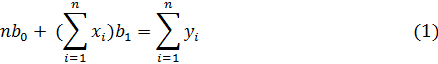
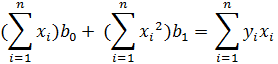
Отримаємо наступну систему:
6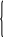 b0+21b1=118
b0+21b1=118
21b0 + 91b1=493,9
Використаємо метод Крамера для розвязку системи. Отримаємо:
∆ =
![]() = 546 – 441 = 105
= 546 – 441 = 105
∆b0
=
![]() = 10738 – 10371.9 = 366,1
= 10738 – 10371.9 = 366,1
∆b1=
![]() = 2963,4 – 2478 = 485,4
= 2963,4 – 2478 = 485,4
b0 = 366,1/105 = 3,48667 b1 = 485,4/105 = 4,62286
Рівняння парної регресії матиме вигляд:
= 3,48667 +4,62286*х
Також для визначення параметрів лінії регресії можна використати оператор вигляду (2) :
B= (XT*X)-1* XTY (2)
З наведених даних (Таблиця 1) випливає, що матриця Х має вигляд:
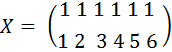
Виконаємо подальші перетворення:
ХT*X=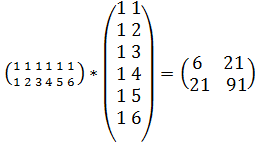 Перевіримо
чи існує матриця обернена до ХT*X,
для цього знайдемо її визначник:
Перевіримо
чи існує матриця обернена до ХT*X,
для цього знайдемо її визначник:
∆ =
=![]() = 0
= 0
Отже, можна зробити висновок, що обернена матриця існує знайдемо її :
(ХT*X)
-1=
![]()
Знайдемо матрицю ХT*Y:
ХT*Y
= ![]()
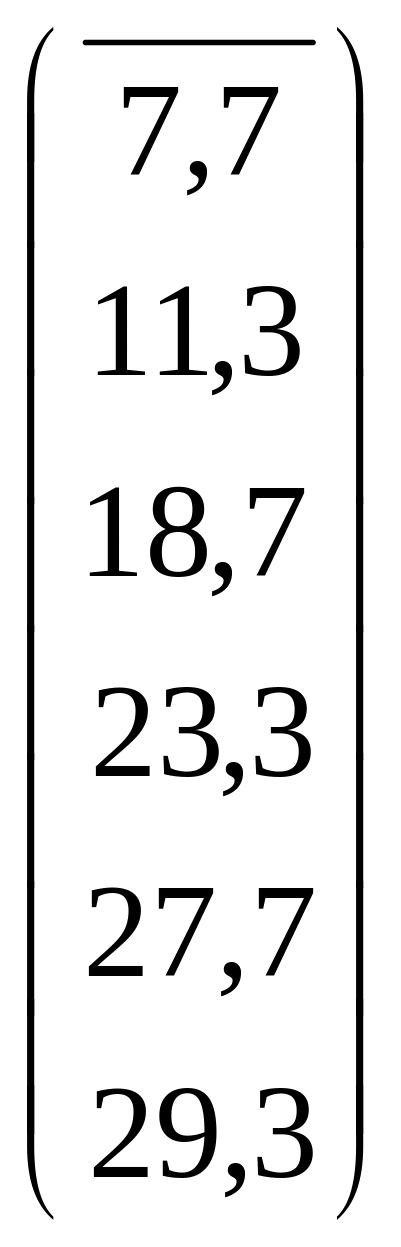 =
=
![]()
B
= ![]()
![]() =
=
![]()
b0 =3,4906 b1=4,6017
Рівняння парної регресії при таких даних матиме вигляд:
= 3,4906 +4,6017*х
2 .
Для обчислення інших параметрів регресії
сформуємо додаткову талицю:
.
Для обчислення інших параметрів регресії
сформуємо додаткову талицю:
Y = 118÷6= 19,66667
№ |
Уі |
Хі |
Хі2 |
Хі*Уі |
|
Уі - |
(Уі - )2 |
Уі
-
|
- |
(Уі - )2 |
|
|
( - )2 |
1 |
7,7 |
1 |
1 |
7,7 |
8,10953 |
-0,40953 |
0,167715 |
-11,96667 |
-11,55714 |
143,20119 |
|
|
133,56748 |
2 |
11,3 |
2 |
4 |
22,6 |
12,73239 |
-1,43239 |
2,051741 |
-8,36667 |
-6,93428 |
70,00117 |
|
|
48,08424 |
3 |
18,7 |
3 |
9 |
56,1 |
17,35525 |
1,34475 |
1,808353 |
-0,96667 |
-2,31142 |
0,93445 |
|
|
5,34266 |
4 |
23,3 |
4 |
16 |
93,2 |
21,97811 |
1,32189 |
1,747393 |
3,63333 |
2,31144 |
13,20109 |
|
|
5,34275 |
5 |
27,7 |
5 |
25 |
138,5 |
26,60097 |
1,09903 |
1,207867 |
8,03333 |
6,93430 |
64,53439 |
|
|
48,08452 |
6 |
29,3 |
6 |
36 |
175,8 |
31,22383 |
-1,92383 |
3,701122 |
9,63333 |
11,55716 |
92,80105 |
|
|
133,56795 |
Σ |
118 |
21 |
91 |
493,9 |
118,00008 |
-0,00008 |
10,68419 |
-0,00002 |
0,00006 |
384,67333 |
|
|
373,98961 |
Розрахуємо дисперсію залишків (залишкову дисперсію), враховуючи, що m=1 ( одна пояснювальна змінна), :
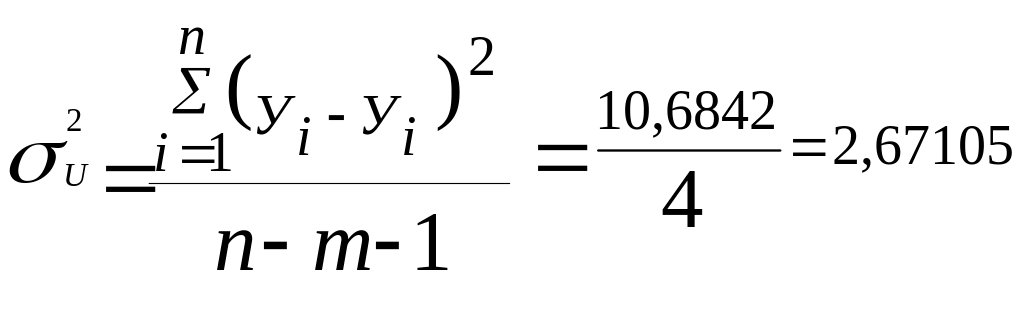
Визначимо стандартну похибку за формулою:
S
= ![]() =
=
![]() =1.63433
=1.63433
Це значення у нас також міститься у таблиці статистики функції ЛИНЕЙН у другій комірці третього рядка.
Перевіримо тісноту загального впливу незалежної змінної на незалежну змінну, обчисливши коефіцієнт детермінації R2 :
![]() =
373,98961/384,67333
= 0,97223
=
373,98961/384,67333
= 0,97223
Таке ж значення міститься і в таблиці статистики функції ЛИНЕЙН в першій комірці третього стовпчика.
Тоді коефіцієнт кореляції можна розрахувати так:
![]()
Оскільки коефіцієнт детермінації R2 = 0,97223, це свідчить, що варіація залежної змінної У на 97,2% визначається варіацією незалежної змінної Х. Коефіцієнт кореляції 0,98602 характеризує тісний зв’язок між цими показниками. Величини R2 і R для парної економетричної моделі свідчать про її достовірність, якщо вони наближаються до одиниці.
Перевіримо на значущість вибірковий коефіцієнт кореляції за допомогою t-статистики.
Кореляція – це систематичний і зумовлений зв'язок між двома видами явищ (факторів).
