2.2. Основные операции над множествами
Над множествами выполняются теоретико-множественные операции, в результате которых образуются новые множества: объединение, пересечение, разность, симметрическая разность, дополнение. Эти операции являются способами конструирования новых множеств из заданных множеств.
Рассмотрим
два произвольных множества: множество
и множество
.
Допустим, что каждому элементу множества
ставится в соответствие свойства
,
а каждому элементу множества
ставится в соответствие свойство
.
Таким образом, каждый элемент множества
и
обладает соответственно свойством
и
.
2.2.1. Объединение множеств
Под объединением
множеств
и
будем понимать множество, обозначаемое
и состоящее из таких элементов, которые
обладают хотя бы одним из свойств:
или
.
Высказывательная форма операции
объединения множеств имеет вид:
.
Таким
образом, элемент
принадлежит объединению множеств
тогда и только тогда, когда этот элемент
принадлежит хотя бы одному из множеств:
или
.
Если обозначить отношение «тогда и
только тогда» символом
,
то высказывательная форма последнего
выражения имеет следующий вид:
.
Приведённые высказывательные формы
содержат логическую операцию дизъюнкции
,
рассматриваемую нами ранее при изучении
функций алгебры логики. При этом
отмечалось, что операция дизъюнкции
выполняется над логическими переменными
,
принимающими значения из двухэлементного
множества
:
.
В применяемых же нами высказыватнльных
формах для объединения множеств операция
дизъюнкции выполняется над некоторыми
выражениями:
и
.
Возникает вопрос о правомерности
использования логической операции над
выражениями. Приведём обоснование этой
правомерности в выражении
.
Слева и справа от знака
стоят так называемые высказывания. В
логике под высказыванием понимают любое
языковое предложение, относительно
которого говорят об его истинности или
ложности. Таким образом, в математической
логике интересуются не содержанием
предложения, а его истинностным значением.
В двузначной логике в качестве множества
истинностных значений принято
двуэлементное множество
,
элементы которого интерпретируются
как «ложь», «истина». Принятие
высказываниями
и
значений из множества
и обосновывают правомерность выполнения
над ними операции дизъюнкции. Применим
выражение
для геометрической интерпретации
операции объединения множеств в виде
диаграммы Венна. Истинность выражения
,
стоящего справа от знака
,
должна повлечь за собой истинность
выражения
,
стоящего слева от этого знака. Но
результат операции «дизъюнкция» между
двумя переменными принимает значение
«истина», если хотя бы одна переменная
принимает значение «истина». При этом
могут представиться следующие варианты:
- высказывание
принимает значение «истина», а высказывание
принимает значение «ложь» (на рис. этому
варианту соответствуют точки
и
);
- высказывание
принимает значение «ложь», а высказывание
принимает значение «истина» (на рис.
этому варианту соответствуют точки
,
);
-
высказывание
и высказывание
принимают значение «истина» (на рис.
этому варианту соответствуют точки
,
).
Перечисленные варианты истинностных значений высказываний определяют диаграмму Венна, представленную на рис. 2.2.
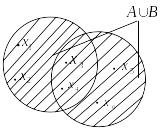
Рис. 2.2. Диаграмма Эйлера операции объединения множеств
Операция объединения может быть распространена и на большее количество множеств:
.
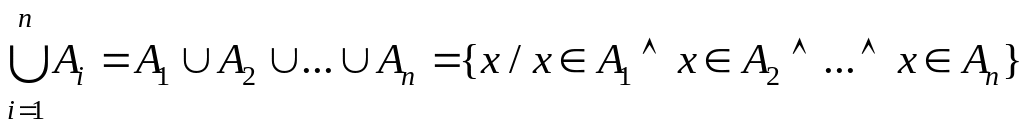Пример 2.1
Рассмотрим два множества, заданных перечислением своих элементов:
и
.
Объединение
множеств
и
представляет собой следующее множество:
.