Параграф 1.5. Вынужденные колебания. Переходный процесс.

Решения, полученные в параграфе 1.4, уравнение вынужденных колебаний не зависит от начальных условий и поэтому не является единственным и общим – это частное решения уравнения.

Для того, что бы найти общее решение заметим, что сумма решений нашего уравнения и уравнения затухающих колебаний

будет являться решением уравнения вынужденных колебаний, для того, что бы в этом убедиться подставим в уравнение решение.

Мы учли, что уравнение затухающих колебаний имеет вид:

- определяется параметрами системы, а -

являются произвольными и определяются изначальными условиями, поэтому полученное решение является общим и единственным при заданных начальных условиях.

Таким образом мы нашли 2 произвольные величины, которые удовлетворяют нулевым начальным условиям.

Тогда решение будет иметь вид:

Т.к. , то знак + не подходит.

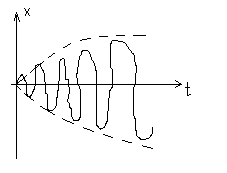
Таким образом, полученное решение состоит из 2х частей, при этом вторая часть решения с течением времени уменьшается, и через время релаксации практически исчезает. И начиная с этого времени в системе будут наблюдаться колебания (формула, для которых, была получена в п. 1.4) при этом говорят, что в системе наблюдается установившийся, или стационарный процесс. Поэтому частное решение из п. 1.4. часто называют стационарным решением. Это решение от начальных условий не зависит, если , то существуют обе части решения и в системе наблюдается переходный процесс. Форма этого процесса наблюдается начальными условиями. Рассмотрим случай, когда в системе нет затуханий при нулевых начальных условиях, при этом

Тогда ,

Решение будет иметь вид:

т.к. x(0)=0

то

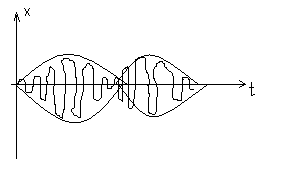
Таким образом, при отсутствии затухания никогда не будет наблюдаться установившееся решение, т.е. в системе все время происходит переходный процесс.

Колебания такого вида называются колебаниями биения.

Параграф 1.6. Сложение гармонических колебаний 2х частот.

В системе с 1ой степенью свободы могут существовать колебания только с 1ой частотой. Для того, что бы в системе могли наблюдаться колебания с различными частотами должно быть много степеней свободы. Если у нас осциллятор с 2мя степенями свободы, то в нём могут наблюдаться колебания с 2мя частотами.

В качестве примера системы с 2мя и 4мя степенями свободы рассмотрим 2 пружинных маятника.

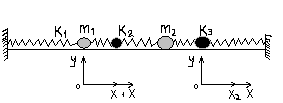
Пусть в положении равновесия все пружины не деформированы, координаты каждой из грузиков будем определять по отношению к его положению равновесия.

Тогда уравнение первого грузика будет:

Эту систему уравнений можно переписать в общем виде:

где

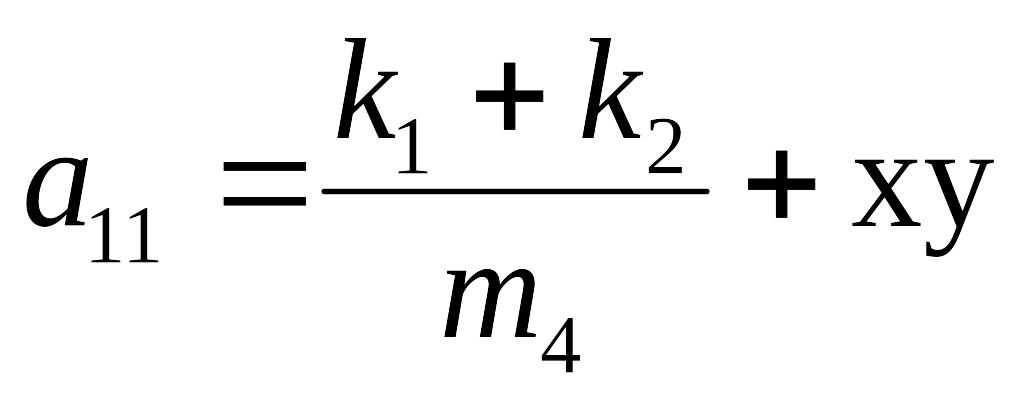
Решение этой системы будем искать в виде:

Как известно система линейных однородных уравнений имеет нетривиальное решение, если ее определитель = 0.

Это условие приводит к биквадратному уравнению для , из четырех корней которых выбираем 2 положительных и .

Тогда решение будет иметь вид

В результате сложения 2^х колебаний получаем биение.

Из математики известно, что систему однородных уравнений

Заменой переменной , а

Можно привести к виду:

т.е.система однородных уравнений распадается на 2 независимых.

Переменные и называются - нормальные координаты

системы.

Такие координаты существуют всегда.

Нормальных координат решение будет иметь вид

т.е. каждая нормальная координата будет изменяться по гармоническому закону с 1^ой собственной частотой и никаких сложений колебаний не происходит.

Таким образом сложение гармонических колебаний в системе с несколькими степенями свободы, при условии что эта система описывается не нормальные координаты.