9.Электрон в периодическом поле. Энергетические зоны.

Рассмотри электрон который находится в периодическом поле, представляет собой последовательность потенциальных ям с интервалом d

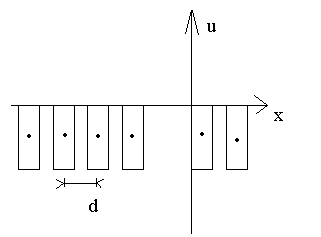
Представим что электрон находится в одной из этих ям когда за счет туннельного эффекта он может попасть в соседние ямы т.е. существует вероятность обнаружить электрон той же самой энергии в любой яме одна и такая же. Зависимость энергии электрона E от волнового числа k в периодическом поле будет практически такая же как у свободного электрона.

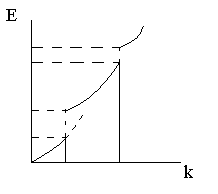
Однако в периодическом поле будут существовать некоторые особенности. Волновая функция электрона на каждой границе ямы. В общем случае электрические волны за исключении когда отрицательные волны находятся в фазе когда геометрическая разность хода будет равна числу волн. Αd=nλ=n2п/k ; k=(п/d)n

При сложении которой с падающей волны возникает стоячая волна. При таких k волновая функция электрона приставляет собой стоячею волну. Т.е. чередование узлов и пучности при этом возможны два варианта :

1. Пучности находятся под ямой

2. Узел находиться под ямой

В первом случае говорят что электрон захвачен ямой. Во втором случае электрон вне ямы. Энергия электрона в этих случаях будет различна, когда электрон в яме его энергия будет меньше чем энергия свободного электрона. Электрон в периодическом поле имеет нейтральный спектр энергии его движения не ограничена, также как и у свободного электрона. Влияния периодического поле приводит к возникновению в непрерывном спектре заряженных зон энергии.

Рассмотрим кристаллическую решетку твердого тела. Потенциальная энергия электрона у каждого узла решетки приставляет собой потенциальную яму. Если твердое тело кристаллическая, то по нему энергия электрона твердого тела будет периодической последовательность потенциальных ям.

Движение электронов в твердом теле будет похоже на движение электрона в периодическом поле.

Отличее состоит в том, что движение электронов в твердом теле ограничено размерами тела, а это означает, что энергия спектра в различных зонах энергии будет дискретным, но из-за того что размеры твердого тела много больше размера электрона, то интервал между ближайшим уровнем энергии будет ничтожно мал и по этому энергия электрона под действием внешнего поля может меняться непрерывно т.е. внешнее поле действует на электрон и его скорость меняется.

Если это не один электрон то картина резко меняется по принципу Паули в одном состоянии может находиться один электрон.

Если все состояния в разрешенной зоне энергетически заключена то энергия электронов под действием внешнего поля изменяться не может. Последняя полностью заполненная зона энергии называется валентной зоной. Специальная зона называется зоной проводимостью. Если между валентной зоной и зоной проводимости ∆ε >> kT , то такое тело называется диэлектриком. Если ∆ε << kT , или валентная зона полностью пустая то такое тело называется проводником. ∆ε = kT такое тело называется полупроводником.

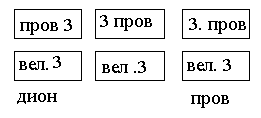
Скорость электрона в твердом теле совпадает с групповой скоростью волны.

V = (1/ћ)(dE/dk) ; a = (dV/dt) = (1/ћ)(d/dt)(dE/dk) = (1/ћ)(d²E/dt²)(dk/dt)=

=(d²E/dt²)(1/ћ²)(d(ћk)/dt) ; P = ћk ; dp/dt = F ; a = (1/ћ²)(d²E/dt²)F ; ma = F

m = h²/ d²E/dk²

Такое представление поведения электрона в твердом теле называется зонной теории. Суть зонной теории состоит в следующем что сложное взаимодействие электронов с внешним полем и с ионами кристаллической решетки заменяется на некоторый ящик с размерами твердого тела в котором нет никаких ионов а есть только электроны. Эти электроны ведут себя точно также как свободные электроны с тем лишь отличием, что в их энергетическом спектре появляются запрещенные зоны энергии.

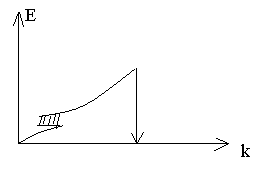
Вместо массы электрона надо использовать ексрентивную массу равную

m = ћ²/d²E/dk²

Зонная теория- это модель которая позволяет все упростить.