23 Універсальний підхід (а-схеми)

У межах універсального підходу існує можливість описувати процеси функціонування неперервних І дискретних, детермінованих і стохастичних об'єктів. Цей підхід базується на понятті агрегат ивної системи (англ. Aggregate system), що є формальною схемою загального вигляду (/(-схему).

При агрегативному описі складний об'єкт (система) розбивається на скінченну кількість частин (підсистем), зберігаючи при цьому зв'язки, що забезпечують їхню взаємодію. У результаті такої декомпозиції складна система подається у впідяді багаторівневої конструкції із взаємозалежних елементів, об'єднаних у підсиеіеми різних рівнів. Елементами Л-схеми виступають агрегат, а зв'язки між агрегатами (всередині системи іа із зовнішнім середовищем) здійснюються за допомогою оператора сполучення

R. Очевидно, що агрегат сам може розглядатися як .-(-схема, тобто може розбиватися па елементи (агрегати) наступного рівня.

Кожен із агрегатів характеризується такими множинами: моментів часу Г. вхідних сигналів X. вихідних сигналів У. станів Z у кожний момент часу (. Стан агрегату в момент часу ієТ позначається як z(t)Ђ.Z, вхідні й вихідні сигнали як x(i)gX і у(0є У відповідно.

Вважається, що перехід агрегату зі стану z(t/) у стан z(i-f*z(ti) визначаються власними (внутрішніми) параметрами самого агрегату /і(і)єН і вхідними сигналами х(і)єХта відбувається за малий інтервал часу, тобто має місце стрибок Sz. Моменти стрибків станів & називають особливими моментами часу Іс$, а стану z(t§) - особливими етапами /(-схеми.

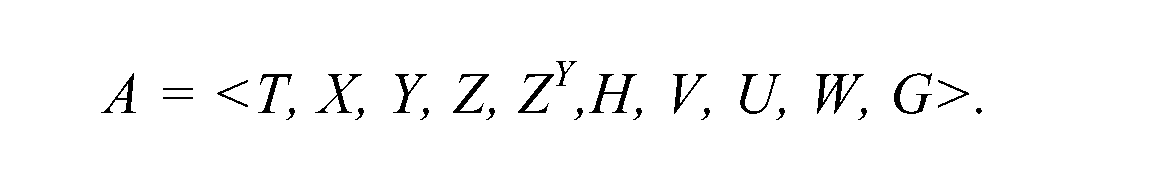
24 Мережсвий підхід.

Для математичного опису процесів функціонування дискретних об'єктів з паралельно та асинхронно взаємодіючими процесами розроблено сітьовий підхід на основі мереж Петрі (K.Petri).

Мережа Петрі моделює процеси, що подаються у вигляді послідовності подій. Вона подається у вигляді дводольного орієнтованого графа, який складається з вершин двох видів: позицій І переходів. Позиції відображують умови настання подій, а переходи - власне події. Достатні умови настання подій подаються шляхом розмітки (маркування) позицій мережі.

Вважається, що події настають миттєво і у різний час. Кожній події відповідає перехід мережі. Подія відбувається, якщо виконуються певні умови. Кожній Із умов відповідає певна позиція. Виконання умов відображується за допомогою маркерів (фішок), що позначаються у вигляді точок у середині відповідних позицій. Кількість можливих станів мережі визначається кількістю її можливих маркувань (розподілів маркерів за позиціями).

Моделювання мережею Нетрі відображується переміщенням маркерів між позиціями р,. Послідовність подій відображується як послідовність спрацювань (збуджень, запусків) переходів uf. Подія / наступає (перехід ut спрацьовує), якщо маркери присутні у всіх вхідних позиціях р, переходу. Здійснення події / відображаується у вилученні маркерів із усіх вхідних позицій переходу иf та поміщенні ного у всі вихідні позиції цього переходу.

Формально мережа Петрі (.V-схсма, від англ. Net — мережа) подається як кортеж, що має такий вигляд:

N=<P, U,F,H,Me>, (4.11)

де Р = {pi} - скінченна непуста множина позицій:

U = {и)f - скінченна непуста множина переходів;

F = PxU-*{0,l} вхідна функція інцидентності. яка вказує на наявність дуг, що пов'язують позиції з переходами;

Н'= U х Р-* {0, - вихідна функція інцидентності, яка вказує на наявніс і ь луї, що пов'язують переходи з позиціями;

Мц - початкова розмітка мережі, Мд: Р —> f(), І, 2, ...}, яка визначає початкове розміщення маркерів на позиціях мережі.