8 Ідентифікація за методом найменших квадратів.

Метод найменших квадратів

Нехай у моменті часу t₀, t­₁, … t_n і u(t_i) – вхідні сигнали y(t_i) – вихідних сигналів ,за відсутності додаткової інформації використовується метод найменших квадратів

Якщо є додаткова інформація щодо точності вимірювань доцільно використовувати метод найменших зважених квадратів

Критерії найменших зважних квадратів

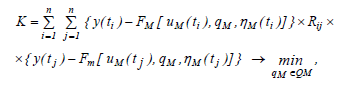
Rij – елемент коваріаційної матриці.

Для пошуку найкращого значень параметр треба розв’язати матрицю

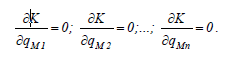
9, Формалізація опису системи: мста, критерії,обмеження.

Формалізація опису системи

Формалізація – подання опису формального(штучного) мовою(математичною) На ранніх етапах моделювання об’єкт подається як система

S =<E, R> (*) – об’єкт ‘ у вигляді системи

E –множина об’єктів

R- множина відношень

(*) має множину властивостей P=φ(E,R) (**).

Позначимо універсальні множини елементів (ті які охвачують ) E –елементи, R- відношення, P- властивості. На першому етапі виділяються найбільш важливі властивості об’єкта, які в подальшому формалізується і використовуються як часткові критерії оптимізації. Р_ф Р, E,R , E_c E R_c R - называють область існування

Виходячи з технічних,економічних, політичних, екологічних обмежень і т.д. область снувань звужується до E_g, R_g , - до допустимих. На останньому етапі постає питання вибору найкращого варіанту системі із областей

S⁰=<E⁰,R⁰> E⁰c E_g, R⁰ c R_g, тепер,що задовольняє умовам P P_ф .

Серед показників P_ф виділяють підмножини що характеризують ефект і витрати

Q={k₁,k₂,…., k_m­}ефект

C={k_m+1, … , k_n}витрати

Причому у загальному вигляді

в

_

Q

_

C

_

Q

_

C

иникає задача вибору наилучшего вариант построении системи за комплексними показником ,

S⁰=arg extr Q[ , , F] (***)

= F( )

Ф

_

Q

_

C

ункціонал – функція от функції.

Н

_

C

_

Q

а практиці через складність, зводиться до однієї задачі

S⁰=arg max(/S є S*) Q[ , <=C^*] – задача max ефективності

S⁰= arg min (/S є S*) Q` [ , <=Q*] – мінімум затрат

S* - допустимые расходы

10 Прийняття рішень за результатами моделювання.

Задача прийняття рішень

Глобальною метую моделювання : підвищення ефективності існуючої або створення максимально ефективної. Задача прийняття рішень формулюються в термінах ситуація мета, ситуація описує поточний стан а мета бажаний.

Розрізняють задачі прийняття рішень в умови

• Ризику

• Визначені

• Невизначеності

Задача в умовах визначеності в вибору альтернативи x є X що однозначно приводить до одного наслідку множин u -> U

В умовах ризику при вибору x⁰ є X приводить до різних наслідків u₁є U, u₂ є U,…, u_n є U з різною точністю.

В умовах невизначеності x⁰ є X приводить до різних наслідків u є U з невідомими ймовірностями

Для розв’язання задач є 2 під хода: ордіналістичний і кардіналістичний . В рамках першого підходу, альтернативні варіанти впорядковуються за корисністю(цінністю ). x₁ x₂ …x_n

В рамках кардінастилістинчному підходу дається кількісна оцінка його корисності чілостності тоді його варіант .

В рамках першого підходу використовується бінарного відношень. Бігармин відношенням

використовується апарат ошарннх відношень, шнарним відношенням а на непустій множині атьтернатнв Л' називають підмножнну множини всіх упорядкованих пар з X, що задасться прямим добутком Х*Х = {(х,у): х,уєХ}. Запис xRy (х перебуває у відношенні R до >')

означає, що fx, у) належить R: аналогічно не х R у (х R у) означає, що /х, у) не належить R, або що Л" не перебуває у відношенні R до .v.

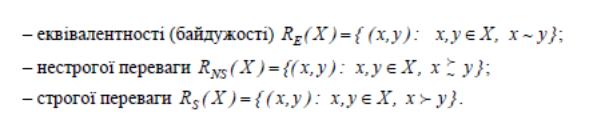- еквівалентності (байдужості) RE1X ) = { іх,у): х,уєХш х~у}\ -нестрогоїпереваги Rys(X) = {(x,y): х,у<=Х, х*у);

- строгої переваги RS(X )-{(х,у): х,у еХ, х> у}.

11 Проблема багатокрнтеріальної оптимізації.

Задачі прийняті я рішень традиційно формалізуються в термінах «умови - мета». При цьому «умови» розглядаюті>ся як множина станів об'єкта й операторів, що переводять його з одного стану в інший, а «мета» як бажаний стан об'єкта. Формально задача полягає у виборі альтернативи хєХ, що призводить до деякого наслідку (результату) мєС? (U - множина можливих наслідків). Ефективність рішення (розв'язку) визначається ступенем відповідності отриманого наслідку ucU поставленій меті й оцінюється за множиною показників (критеріїв).

Основними класами задач прийняття рішень є:

- задача в умовах визначеності - коли кожна альтернатива .тєА' призводить до єдиного наслідку ueUt тобто існує детермінована залежність наслідків від альтернатив;

- задача в умовах ризику - коли кожна з альтернатив хєХ може призводити до одного з декількох наслідків и є Ut з певною ймовірністю;

- задача в умовах невизначеності - коли кожна з альтернатив х є А' може