Задача № 7.

Коллимированный пучок электронов, прошедших ускоряющую разность потенциалов , падает нормально на тонкую поликристаллическую фольгу золота. На фотопластинке, расположенной за фольгой на расстоянии от неё, получена дифракционная картина, состоящая из ряда концентрических окружностей. Радиус первой окружности . Определите: а) брэгговский угол , соответствующий первой окружности; б) длину волны де Бройля электронов ; в) постоянную кристаллической решётки золота.

Решение:

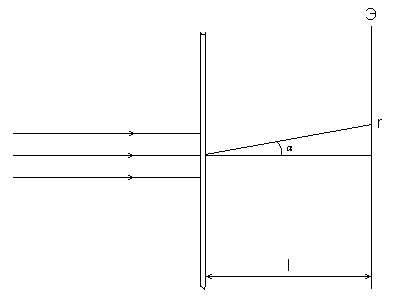
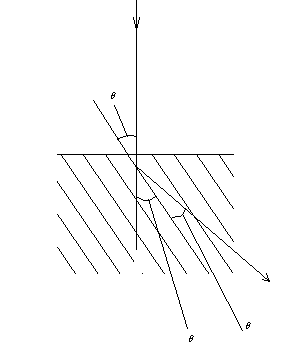
Рисунок 2 Рисунок 1

Используя рисунок 2, определим угол :

(1)

Как видно из рисунка 1, угол , где - брэгговский угол скольжения. Таким образом, мы можем найти брэгговский угол, соответствующий первой окружности:

(2)

Длина волны де Бройля падающих на золотую фольгу электронов:

(3)

где - импульс электронов. Считая электроны релятивистскими, определим их импульс:

(4)

где - кинетическая энергия электрона, а - масса покоя электрона. Тогда дебройлевская длина волны электронов равняется:

(5)

Воспользуемся условием Вульфа-Брэггов:

(6)

где - постоянная кристаллической решётки, - порядок максимума (в нашем случае максимум первого порядка ). Найдём из выражения (6) постоянную кристаллической решётки, учитывая, что значение и определяются соответственно выражениями (2) и (5):

(7)

Ответ:

а)

б)

в) .

Задача № 8.

Параллельный пучок электронов, ускоренный разностью потенциалов , падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми . Определите расстояние между соседними максимумами интерференционной картины на экране, отстоящим от щелей на расстоянии .

Решение:

Найдём длину волны де Бройля, соответствующую электрону:

(1)

где - импульс электрона, - его кинетическая энергия. Таким образом, длина волны де Бройля электрона:

(2)

На рисунке 1 представлена схема установки:

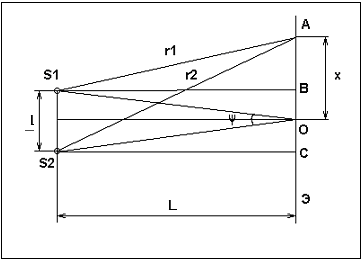
Рисунок 5

S1 и S2 –щели (вторичные источники). В результате интерференции волн от этих двух вторичных источников на экране появляется интерференционная картина. Из прямоугольных треугольников и по теореме Пифагора:

(3)

(4)

Вычтем из уравнения (4) уравнение (3):

(5)

Но, так как , где - оптическая разность хода двух интерферирующих волн , а , так как , то мы можем записать:

(6)

Если оптическая разность хода двух волн равна целому числу волн , то образуется максимум. Используя уравнение (6) и условие максимумов, определим положение максимумов на экране :

(7)

Тогда расстояние между соседними максимумами:

(8)

Подставим в выражение (8) дебройлевскую длину волны электронов, падающих на диафрагму, получим:

(9)

Подставляя числовые значения, получим:

Ответ:

.