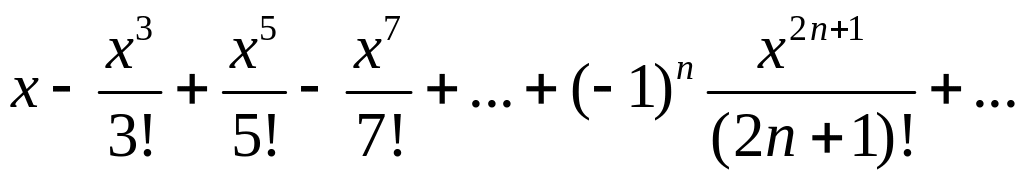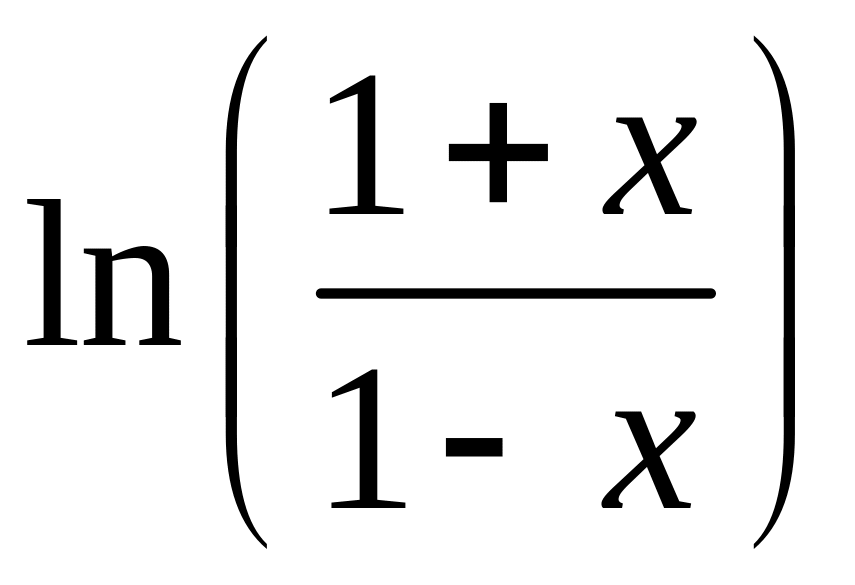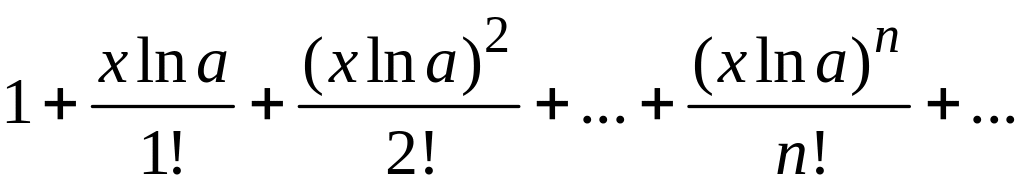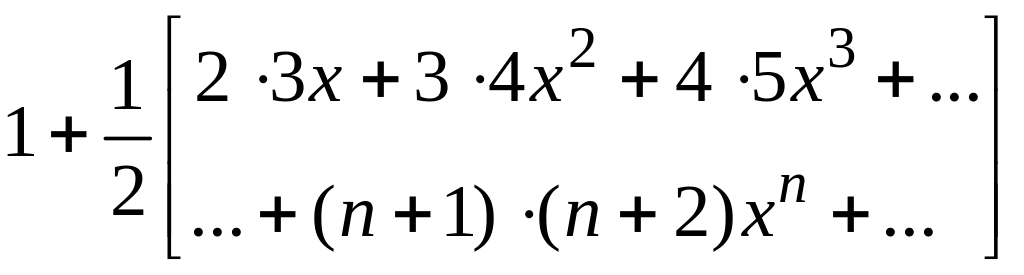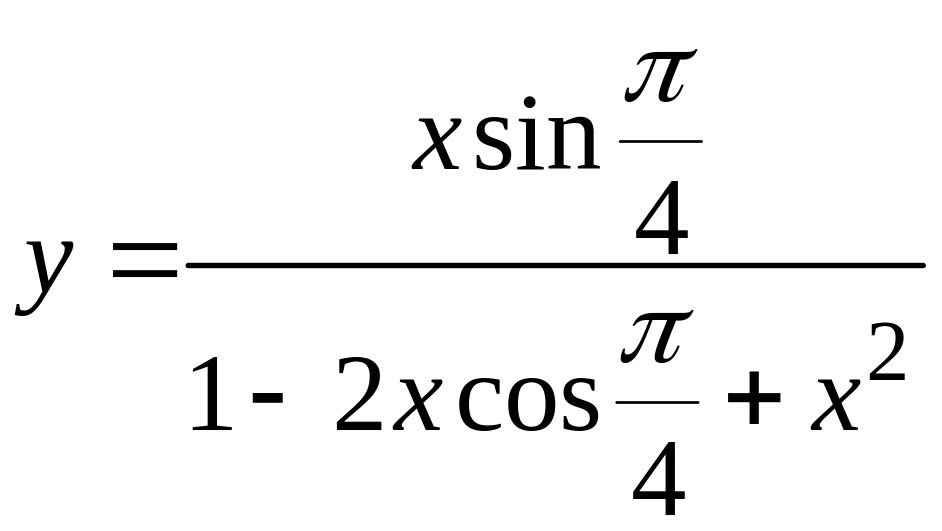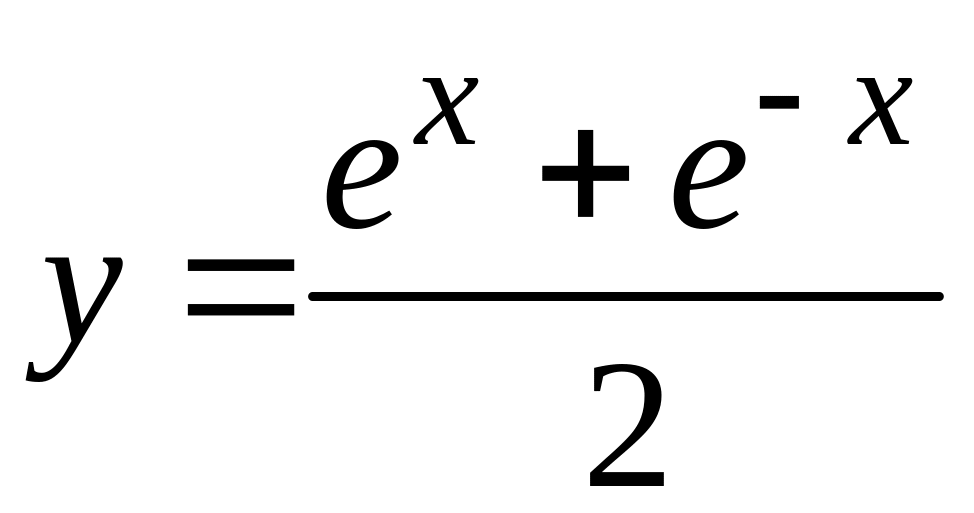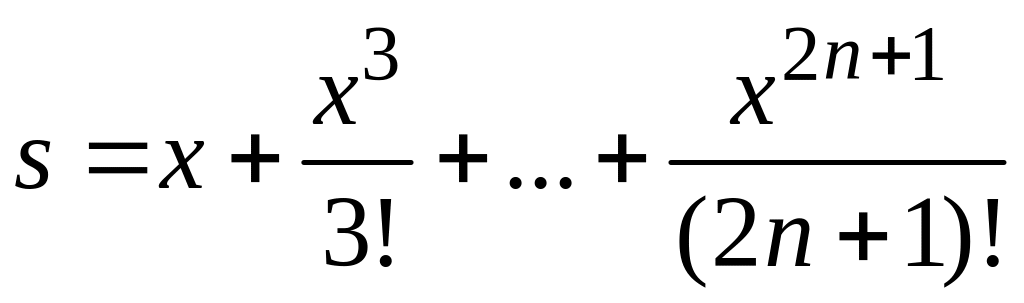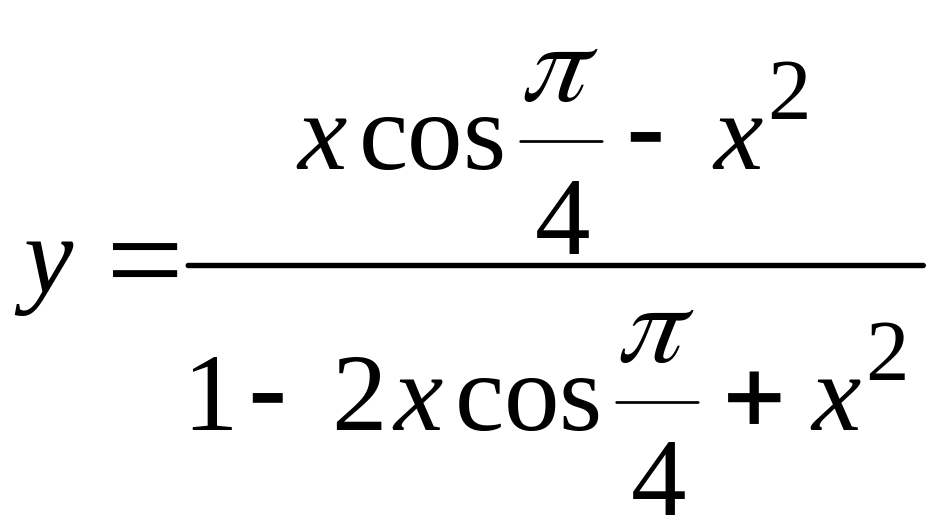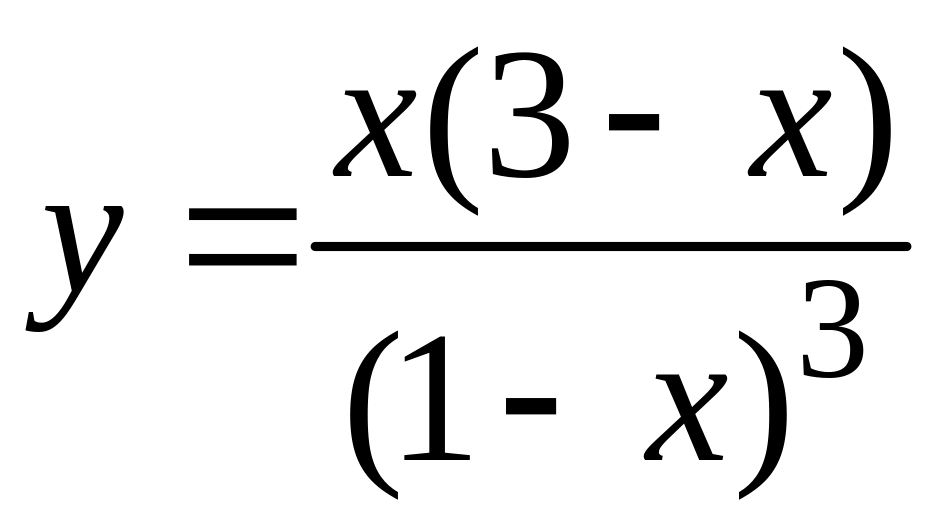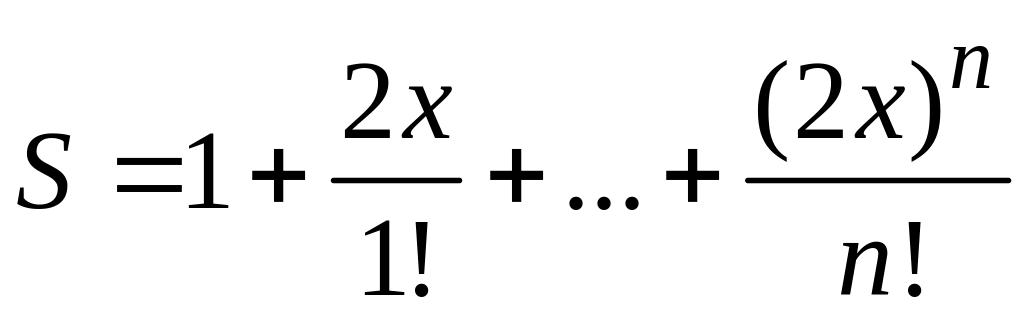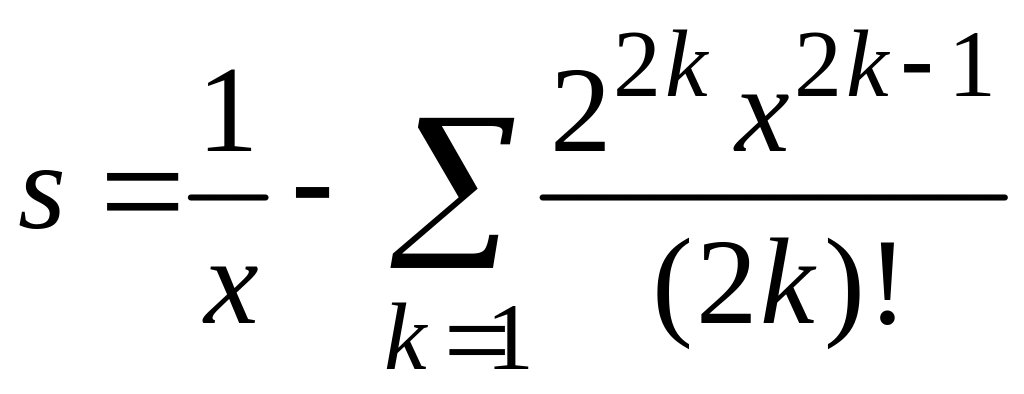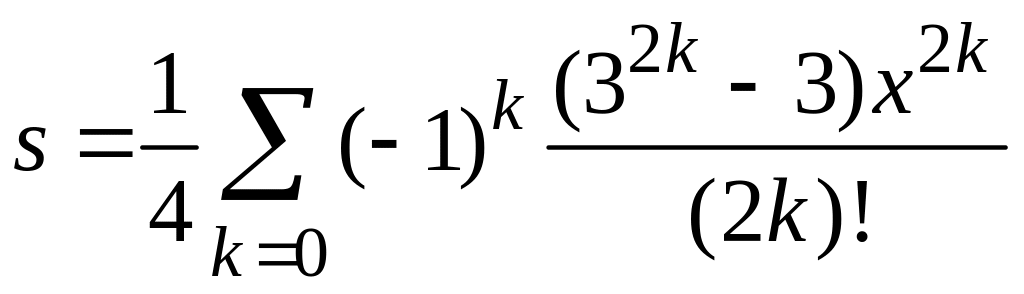9.4 Вычисление сумм числовых рядов Вычисление конечных сумм

Краткое теоретическое введение.

Задача вычисления конечных сумм сводятся к нахождению суммы некоторого количества слагаемых s=Σ a_n(x) при различных значениях параметра суммирования х. Каждое слагаемое суммы зависит от параметра х и номера п, определяющего место этого слагаемого в сумме.

Обычно формула общего члена суммы принадлежит к одному из следующих трех типов:

а)

б)

в)

В случае а) для вычисления члена суммы целесообразно исполь­зовать рекуррентные соотношения, т. е. выражать последующий член суммы через предыдущий. Это позволит существенно сократить объем вычислительной работы. Кроме того, вычисление члена суммы по общей формуле в ряде случаев невозможно (например, из-за наличия п!).

В случае б) применение рекуррентных соотношений нецелесооб­разно. Вычисления будут наиболее эффективными, если каждый член суммы вычислять по общей формуле.

В случае в) член суммы целесообразно представить в виде двух сомножителей, один из которых вычисляется по рекуррентному соотношению, а другой — непосредственно. Например:

то полагаем c_n=x⁴ⁿ⁺¹ и вычисляем c_n= c_n-1 х⁴, а - непосредственно.

Алгоритм решения задач суммирования при значениях параметра суммирования, изменяющегося в некотором диапазоне с заданным шагом, сводится к двум вложенным циклам. Внутренний цикл сум­мирует слагаемые при фиксированном параметре х, а внешний орга­низует изменение параметра х. Для всех вариантов, вычисляемая сумма является частичной суммой некоторого функционального ряда, поэтому наряду с вычислением суммы необходимо вычислять (для сравнения) и функцию y=f(x) (сумму функционального ряда).

Диапазон изменения аргумента х задан в виде а х b. Для каждого варианта вычисление суммы проводится для следующих значении аргумента х = а, a+h, …, a+9h, b, где h=(b-a)/10

Пример 9.4.1. (случай б)

Составить программу для вычисления суммы

(n=50) (9.1)

и функции: при 0,1 х 0,8 с шагом 0,1

Перепишем (9.1) в виде:

(9.2)

/***************************************************/

/* Выисление суммы ряда */

/************************************ **************/

#include <stdio.h>

#include <conio.h>

#include <math.h>

void main()

{

float a,b,h; //a- начало, b- конец, h-шаг

float c,s,x,y; // с- общий член, s-сумма ряда,

// x- аргумент функции,

// y- значение функции

int k,n; // k - параметр, n- кол-во членов ряда

clrscr();

printf("\n начало: а="); scanf("%f",&a);

printf(" конец: b="); scanf("%f",&b);

printf(" шаг: h="); scanf("%f",&h);

printf(" кол-во членов ряда: n=");

scanf("%d",&n);

printf("\na=%.2f\tb=%.2f\th=%.2f\t\n=%d",a,b,h,n);

for(x=a; x<=b+h/1000; x=x+h)

{

s=0;

for(k=1; k<=n; k++)

{

c=cos(2*k*x)/(4*k*k-1);

s=s+c;

}

y=0.5-M_PI/4*fabs(sin(x));

printf("\n x=%.2f \t s=%f \t y=%f",x,s,y);

}

getch();

}

Результаты работы программы:

начало: а=0.1

конец: b=0.8

шаг: h=0.1

кол-во членов ряда: n=50

a=0.10 b=0.80 h=0.10 n=50

x=0.10 s=0.421368 y=0.421591

x=0.20 s=0.344198 y=0.343965

x=0.30 s=0.267746 y=0.267899

x=0.40 s=0.194210 y=0.194152

x=0.50 s=0.123480 y=0.123460

x=0.60 s=0.056464 y=0.056531

x=0.70 s=-0.005891 y=-0.005967

x=0.80 s=-0.063464 y=-0.063410

Пример 9.4.2. (случай а)

Составить программу для вычисления суммы ряда:

(9.3)

и функции у=cos(x)+x sin(x) при 0 х 1 с шагом h=0,1

Перепишем формулу (9.3) в виде:

Общий член суммы относится к типу а).

Выразим (n+1)-й член через n-й:

Найдем коэффициент для рекуррентного отношения:

coef = a_n+1/a_n

= , где n=0,1, …, 9, а₀=1.

Вычисление суммы будем осуществлять с помощью рекуррентной формулы: s_n= s_n-1 + a_n, n=0,1, …, 9, s₀=1.

#include <stdio.h>

#include <conio.h>

#include <math.h>

void main()

{

float a,b,h; //a- начало, b- конец, h-шаг

float c,s,x,y; // с- общий член, s-сумма ряда, x- аргумент функции,

// y- значение функции

int k,n; // k - параметр, n- кол-во членов ряда

clrscr();

printf("\n начало: а="); scanf("%f",&a);

printf(" конец: b="); scanf("%f",&b);

printf(" шаг: h="); scanf("%f",&h);

printf(" кол-во членов ряда: n="); scanf("%d",&n);

printf("\n Введено:a=%.2f \t b=%.2f \t h=%.2f \t n=%d",a,b,h,n);

for(x=a; x<=b+h/1000; x=x+h)

{

s=1;

c=1;

for(k=0; k<=n; k++)

{

c=-c*x*x/((2*k-1)*(2*k+2));

s=s+c;

}

y=cos(x)+x*sin(x);

printf("\n x=%.2f \t s=%f \t y=%f",x,s,y);

}

getche();

}

Результаты работы программы:

начало: а=0

конец: b=1

шаг: h=0.1

кол-во членов ряда: n=10

Введено:a=0.00 b=1.00 h=0.10 n=10

x=0.00 s=1.000000 y=1.000000

x=0.10 s=1.004987 y=1.004987

x=0.20 s=1.019800 y=1.019800

x=0.30 s=1.043993 y=1.043993

x=0.40 s=1.076828 y=1.076828

x=0.50 s=1.117295 y=1.117295

x=0.60 s=1.164121 y=1.164121

x=0.70 s=1.215795 y=1.215795

x=0.80 s=1.270592 y=1.270592

x=0.90 s=1.326604 y=1.326604

x=1.00 s=1.381773 y=1.381773

Суммирование рядов с заданной точностью.

Если в знакочередующемся ряде абсолютные величины членов убывают и общий член стремиться к нулю, то его сумма по абсолютной величине меньше первого члена; остаток ряда r_n (точность, с которой вычисляется сумма ряда) по абсолютной величине меньше первого из отбрасываемых членов.

Пример 9.4.3 (случай в)

Составить программу для вычисления суммы S с заданной точностью е=10^-6

+…

и функции: при 0 х 0,1 с шагом 0,2

Перепишем сумму в виде:

Общий член суммы относится к типу в): целесообразно вычислять рекуррентно ( ); вычислять непосредственно. Таким образом, для члена суммы имеем: a_n= c_n ; c_n= -c_n-1; n=0,1, ...; c₁=x, а сумма изменяется на ее n-й член, т.е. s_n= s_n-1 + a_n. Суммирование производится до тех пор, пока |c_n | > ε.

#include <stdio.h>

#include <conio.h>

#include <math.h>

void main()

{

float a,b,h; //a- начало, b- конец, h-шаг

float c,s,x,y,e; // с- общий член, s-сумма ряда,

// x- аргумент функции,

// y- значение функции е - точность

int k; // k - параметр

clrscr();

printf("\n начало: а="); scanf("%f",&a);

printf(" конец: b="); scanf("%f",&b);

printf(" шаг: h="); scanf("%f",&h);

printf(" точность: е="); scanf("%f",&e);

printf("\n a=%.2f\tb=%.2f\th=%.2f\t e=%f",a,b,h,e);

for(x=a; x<=b+h/1000; x=x+h)

{

s=x;

c=x;

k=0;

do

{

c=-c*x*x*(2*k+1)/(2*(k+1));

k++ ;

s=s+c/(2*k+1);

}

while(fabs(c/(2*k+1))>e);

y=log(x+sqrt(x*x+1));

printf("\n x=%.2f \t s=%f \t y=%f",x,s,y);

}

getch(); }

Результаты работы программы:

начало: а=0

конец: b=1

шаг: h=0.2

точность: е=0.000001

a=0.00 b=1.00 h=0.20 e=0.000001

x=0.00 s=0.000000 y=0.000000

x=0.20 s=0.198690 y=0.198690

x=0.40 s=0.390035 y=0.390035

x=0.60 s=0.568825 y=0.568825

x=0.80 s=0.732669 y=0.732668

x=1.00 s=0.881374 y=0.881374

Примечание:

Обратные гиперболические функции:

Ареа-синус: y=Arsh(x) =

Ареа-косинус: y=Arсh(x) =

Ареа-тангенс: y=Arth(x) =

Ареа-котангенс: y=Arсth(x) =

9.4.1 Вычислить сумму ряда

№ вар	Сумма ряда	Математическое значение
		ln2
		2
		2/3
		1
		1/2
		2/3

9.4.2 Определить сумму ряда с заданной погрешностью ξ для произвольно заданного аргумента x. Определить число повторений итерациионного цикла.

№ вар	Бесконечная сумма	Диапазон	Выражение для проверки
			ех
			cos x
			sin x
			aх
			– ln(1 – x)
			ln(1 + x)
			ln x
			arctg(x)

9.4.3 Вычислить сумму и функцию

№ вар	Сумма и функция	Диапазон	Шаг	n

9.4.4 Вычислить сумму с заданной точностью и функцию в заданном диапазоне

№ вар	Сумма и функция	Точ-ность	Диапазон	Шаг