
- •Лекция 5.1. Основные определения
- •5.1.1. Основные определения теории графов
- •5.1.2. Некоторые виды графов
- •5.1.4. Маршруты, цепи, циклы
- •Определение. Простой цикл с р вершинами обозначается Ср . Например, граф – это одновременно граф с3.
- •5.2.2. Матрица смежности графа
- •3.2.4.Матрица инцидентности графа
3.2.4.Матрица инцидентности графа
Матрица инцидентности неориентированного графа.
Пусть – неориентированный граф с р вершинами и q ребрами. Произвольно переномеруем его вершины и ребра.
Определение. Матрицей инцидентности графа называется матрица с р строками (каждая строка соответствует одной из вершин графа) и q столбцами (каждый столбец соответствует одному из ребер графа), элементы которой определяются правилом
![]()
Пример графа и его матрицы инцидентности приведен на рис. 11
j i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
4 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
6 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
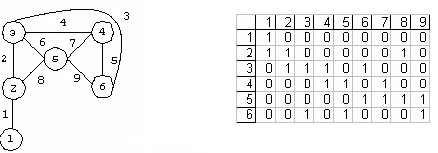
Рис. 11
Свойства матрицы инцидентности неориентированного графа.
Число единиц в i-й строке равно степени i-ой вершины, i = 1, 2, … , р.
Число единиц в -м столбце равно двум, так как любое ребро инцидентно двум вершинам, = 1, 2, …, р.
Число единиц в матрице равно удвоенному числу ребер графа.
Матрица инцидентности ориентированного графа.
Если в орграфе G
р вершин и q дуг,
то элементы
![]() его матрицы инцидентности определяются
правилом
его матрицы инцидентности определяются
правилом
![]()
i = 1, …, p; j = 1, … , q.
Пример орграфа и его матрицы инцидентности показан на рис. 12.
|
12 |
13 |
14 |
23 |
25 |
32 |
34 |
35 |
46 |
56 |
64 |
65 |
1 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
1 |
0 |
0 |
-1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
1 |
0 |
1 |
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
1 |
0 |
5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
-1 |
0 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
-1 |
-1 |
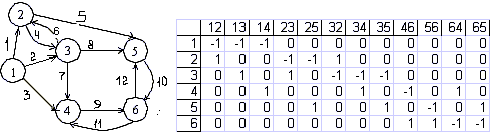
Рис. 12
Свойства матрицы инцидентности орграфа.
Число единиц в i-й строке равно степени входа i-ой вершины, i = 1, 2, … , р.
Число единиц с минусом в i-ой строке равно степени выхода i-ой вершины, i = 1, 2, … , р.
Число единиц в матрице равно числу единиц с минусом и равно числу дуг в графе.
В каждом столбце матрицы есть ровно одна единица и ровно одна единица с минусом, так как всякая дуга из одной вершины выходит и в одну вершину входит.
