Добавил:

guap4736_vkclub152685050 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Сопротивление материалов

Файл:

формула Ясинского.pdf

Скачиваний:

Добавлен:

15.08.2019

Размер:

6.15 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 33

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Изгиб

Плоский (прямой) изгиб — когда изгибающий момент действует в плоскости,

проходящей через одну из главных центральных осей инерции сечения, т.е. все силы

лежат в плоскости симметрии балки. Основные гипотезы (допущения): гипотеза о

не надавливании продольных волокон: волокна, параллельные оси балки,

испытывают деформацию растяжения – сжатия и не оказывают давления друг на

друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское

до деформации, остается плоским и нормальным к искривленной оси балки после

деформации. При плоском изгибе в общем случае возникают внутренние силовые

факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0,

если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются,

М>0

Q>0

снизу

растягиваются.

M ydF; Q ydF; N

Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью,

линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения:

E y

, — радиус кривизны нейтрального слоя, y — расстояние от некоторого

волокна до нейтрального слоя. Закон Гука при изгибе:

, откуда (формула

E J

Навье):

M y

, Jx — момент инерции сечения относительно главной центральной

оси, перпендикулярной плоскости изгибающего момента, EJx — жесткость при

изгибе,

— кривизна нейтрального слоя.

max

Максимальные

напряжения

при

изгибе

возникают

в точках,

наиболее

нейтр.ось

удаленных

от

нейтрального

слоя:

max

M ymax

Jx/ymax=Wx—момент

J x

сопротивления

сечения

при

изгибе,

Если

сечение

не имеет

max

горизонтальной оси симметрии,

то эпюра нормальных напряжений не

будет симметричной. Нейтральная ось сечения проходит через центр

тяжести сечения. Формулы для определения нормального напряжения

нейтр.ось

для чистого

изгиба

приближенно

годятся

когда Q 0. Это случай

max поперечного

изгиба.

При

поперечном

изгибе,

кроме изгибающего

момента

М,

действует поперечная сила Q и в сечении возникают не

только нормальные , но и касательные

напряжения.

Касательные напряжения

определяются формулой Журавского:

Q Sx (y)

, где Sx(y) — статический момент

b(y)

J x

относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии "y" от нейтральной оси; Jx — момент инерции

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в

слое, на котором определяются касательные напряжения.

Для

прямоугольного

сечения:

max

3 Q ,

F=b h,

для

круглого

2 F

max

4 Q

сечения:

max

, F= R , для сечения любой формы max

k— коэфф., зависящий от формы сечения (прямоугольник: k= 1,5; круг - k= 1,33).

Mmax

Qmax

скачок = R

определяются

из

скачок = R

эпюр

изгибающих

скачок = P

моментов

скачок = M

поперечных

сил.

экстремум

эпюра Q

Для

этого

балка

разрезается

на

две

части

эпюра M

рассматривается

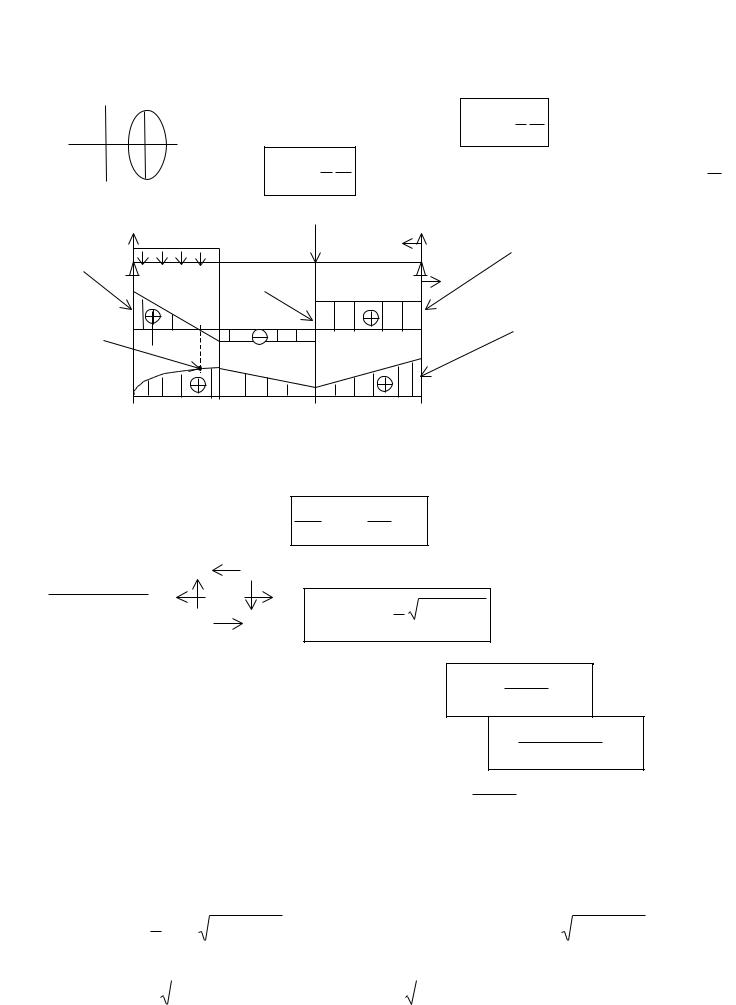
одна из них. Действие отброшенной части заменяется внутренними силовыми

факторами М и Q, которые определяются из уравнений равновесия. В некоторых

вузах момент М>0 откладывается вниз, т.е. эпюра моментов строится на растянутых

волокнах.

При

Q= 0 имеем

экстремум эпюры

моментов.

Дифференциальные

зависимости между М,Q и q:

q — интенсивность распределенной нагрузки [кН/м]

Главные напряжения при поперечном изгибе:

max

min

Расчет на прочность при изгибе: два условия прочности, относящиеся к различным

[ ]

точкам балки: а) по нормальным напряжениям

max

(точки наиболее

max

удаленные от С);

б)

по касательным напряжениям

Qmax Smax

[ ] , (точки на

b J x

нейтр.оси). Из а) определяют размеры балки:

max

, которые проверяют по б).

[ ]

В сечениях балок могут быть точки, где одновременно большие нормальные и

большие касательные напряжения. Для этих точек находятся эквивалентные

напряжения, которые не должны превышать допустимых. Условия прочности

проверяются по различным теориям прочности

I-я:

эквI

1 [

4 2 ] [ ];

II-я:

эквII

0,35 0,65[

4 2 ] [ ]

(при

коэфф.Пуассона =0,3); — применяются редко.


III-я:	эквIII	2 4 2 ] [ ]		, IV-я:	эквIV	2 3 2 ] [ ]		,

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

теория Мора:

эквM

1 m

] [ ],

[

]

(используется для

[

]

чугуна, у которого допускаемое напряжение на растяжение [ р] [ с] – на сжатие).

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

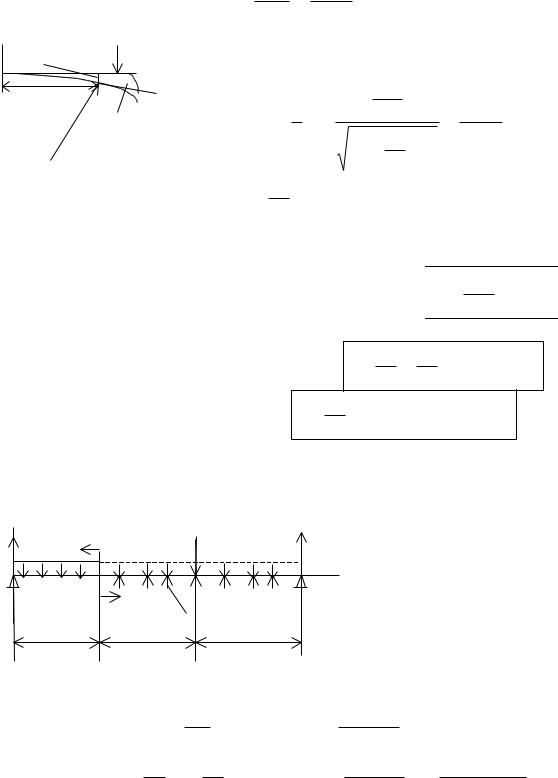
Определение перемещений в балках при изгибе

Имеем закон Гука при изгибе:

1(x)

M(x)

E J x

, где (х) — радиус кривизны изогнутой

y		F
	y, прогиб		x
			x
	x
	x
		, угол поворота
		сечения

оси балки в сечении х, М(х) — изгибающий момент в том же сечении, EJ — жесткость балки. Из высшей математики

		d	2	y
	1	d		y					M(x)
	1	dx		2					M(x)
				2
известно:			dy						EJ	— дифференциальное
		[1 (	dy		)	2	]	3	EJ
						2		3
			dx
			dx

уравнение изогнутой оси балки.

dy dx

— тангенс угла между осью х и касательной к

изогнутой оси. Эта величина очень мала (прогибы балки малы) ее квадратом пренебрегают и угол поворота сечения приравнивают тангенсу. Приближенное

дифференциальное ур-ние изогнутой оси балки:
дифференциальное ур-ние изогнутой оси балки:

направлена вверх, то знак (+). В некоторых вузах ось

	d	2	y
EJ	d		y	M(x)	. Если ось y
EJ	dx		2	M(x)



y	направляется вниз (—).

Интегрируя дифф. уравнение, получаем:

dy	1	M(x)dx C
dx	EJ

— ур-ние углов

поворота, интегрируем второй раз:

y	1	M(x)dxdx Cx D
	EJ

— получаем ур-ние

прогибов. Постоянные интегрирования С и D находятся из граничных условий, которые зависят от способов закрепления балки.

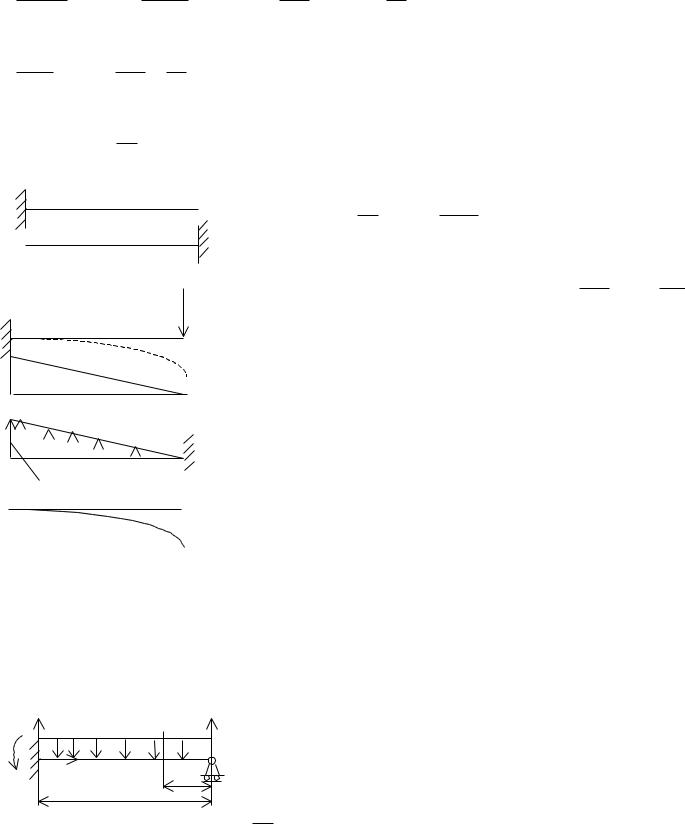
Метод начальных параметров. Начало координат выбирают в крайней левой точке. При включении в уравнение момента


	y	M				М,	который приложен на расстоянии
RA	q	M	P		RB	М,	который приложен на расстоянии
RA						"а"	от	начала		координат, его


A					B x умножают			на	множитель		(х — а)0,
			компенсирующая			который		равен		1.	Любую
	а	b	нагрузка	c		распределенную нагрузку продлевают
	а	b		c		до конца балки, а для ее компенсации
						до конца балки, а для ее компенсации
						прикладывают			нагрузку		обратного

направления. Для рис.:

						x	2					(x a)		2
														2
					q				0	+	q


EJ y = M(x) = RA x –						2		– M(x – a)					2
						2
EJ y			x	2			x	3					(x a)		3
	= EJ 0	+ RA	x		– q		x		– M(x – a) + q				(x a)
	= EJ 0	+ RA	2		– q		6		– M(x – a) + q				6
			2				6						6

– P(x –

– P	(x

a – b);

a b) 2

интегрируем:

;

EJy =EJy0 + EJ 0x + RA	x 3		x 4		(x a)2	+ q	(x a)4		(x a b)3
		– q		– M				– P		.
	6		24		2		24		6

Начальные параметры — то, что мы имеем в начале координат, т.е. для рис.: М0=0, Q0=RA, прогиб y0=0, угол поворота 0 0. 0 находим из подстановки во второе уравнение условия закрепления правой опоры: x=a+b+c; y(x)=0.

заданная балка

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Дифференциальные зависимости при изгибе:

dM(x) dx

Q(x)

;

dQ(x) dx

q(x)

;


	d	2	y
EJ	d		y
EJ	dx			2
				2

M(x)

;

dy dx

Определение перемещений способом фиктивной нагрузки. Сопоставляя уравнения:


2	M
d	M		q
dx		2	q
		2

2	y	M
d
dx	2	EJ

имеем аналогию, определение прогибов можно свести к

определению моментов от некоторой фиктивной (условной) нагрузки в фиктивной

балке:

y=0 =0

Mф=0

Qф=0

qф	M	.
	EJ

фиктивная балка

Момент от фиктивной нагрузки Мф после деления на EJ равен

y 0

прогибу

"y"

в заданной балке от заданной нагрузки.

Qф , получаем,

Учитывая,

что

что угол

M 0

поворота

заданной

балке

численно равен

фиктивной

Q 0

поперечной силе в фиктивной балке.

					При этом должна быть полная аналогия в граничных
					условиях двух балок. Каждой заданной балке
		эпюра М			соответствует своя фиктивная балка. Закрепление
		эпюра М			соответствует своя фиктивная балка. Закрепление
					фиктивных балок выбирается из того условия, чтобы на
					фиктивных балок выбирается из того условия, чтобы на
			фиктивная		концах балки и на опорах имелось полное соответствие
			балка		между "y" и " " в заданной балке и Мф и Qф в фиктивной
			балка

					балке. Если эпюры моментов как в действительной, так и в
	фиктивная				фиктивной балках строить со стороны растянутого волокна
	нагрузка
	нагрузка
					(т.е. положительный момент откладывать вниз), то линии
					прогибов в заданной балке совпадает с эпюрой моментов в

		эпюра М
		эпюра М
				Ф	фиктивной балке.
					фиктивной балке.
Статически неопределимые балки.

Статически неопределимыми называются системы, реакции в которых не могут быть определены из уравнений равновесия твердого тела. В таких системах больше связей, чем это необходимо для равновесия. Степень статической неопределимости балки (не имеющей промежуточных шарниров – неразрезные балки) равна избыточному (лишнему) числу внешних связей (более трех).

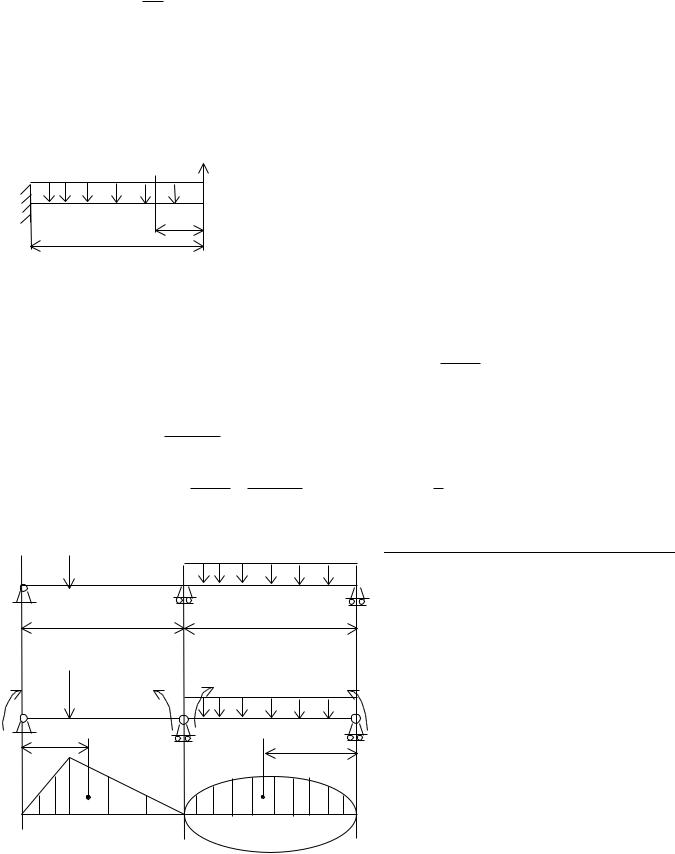
Раскрытие статической неопределимости с помощью дифф-ного урав-ния изогнутой

R		R	оси балки. Записываем дифф-ное урав-ние куда входит в
R		B
A	q		качестве неизвестной реакция RB и дважды его
	q		качестве неизвестной реакция RB и дважды его

	H
MA	A	x
MA		x
		L

интегрируем:

q x 3 + С; 6

	x 2			x 2
= RВ x – q	2 ;	EJ y	= RВ 2		–

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

EJy = RВ		x 3	– q
		6

y	=0; x=L, y=0.

x	4
x		+ С х + D. Используем условия закрепления балки: х=0, y=0,
24		+ С х + D. Используем условия закрепления балки: х=0, y=0,
24

Подставляем их в два последних уравнения, находи постоянные

интегрирования С и D и неизвестную реакцию RB. Далее из урав-ний статики: HA=0;

RA – q L + RB=0; RB L – q	L2	+ MA=0; находятся RA и MA.

2

Уравнение совместности перемещений. Статически определимая балка, которая

основная система	R	получается из статически неопределимой при удалении
	R
q	B	"лишнего" закрепления, называется основной системой.
		"лишнего" закрепления, называется основной системой.

		За "лишнюю" неизвестную можно взять любую из
x		реакций. Приложив к основной системе заданные
L		нагрузки добавляем условие, которое обеспечивает
		совпадение заданной балки и основной – уравнение

совместности перемещений. Для рис.: yB=0, т.е. прогиб в точке В = 0. Решение этого уравнения возможно разными способами.

Способ сравнения перемещений. Определяется прогиб точки В (рис.) в основной

системе под действием заданной нагрузки (q):

yВq=

q L4 8EJ

. Далее рассматривается

основная система под действием "лишней" неизвестной RB, и находится прогиб от

действия RB: yB

R B L3

. Подставляем в уравнение совместности перемещений:

3EJ

yB= yВq + yB

= 0,

т.е.

q L

= 0, откуда RB=

, далее остальные реакции

8EJ

3EJ

находятся из уравнений статики.

Теорема

трех

моментах.

Используется

при

расчете

неразрезных балок — балок на

Ln+1

многих

опорах,

одна

из

которых

неподвижна, остальные подвижны.

основная система

Для

перехода

от

статически

неопределимой балки к статически

Mn-1

Mn+1

определимой основной системе над

–лишними

опорами

вставляются

bn+1

шарниры.

Лишними

неизвестные:

моменты Mn, приложенные к концам

пролетов

над

лишними

опорами.

n+1

Строятся

эпюры моментов

для

эпюра М на n-ом пролете

эпюра М на n+1-ом пролете

каждого пролета балки от заданной

нагрузки,

рассматривая

каждый

пролет, как простую балку на двух опорах. Для каждой промежуточной опоры

"n"

составляется уравнение трех моментов:

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

2 M

) M

6 (

n 1

n 1	b	n 1	)
n 1		n 1
L
L
n 1

n, n+1–площади эпюр,

an – расстояние от центра тяжести левой эпюры до левой опоры, bn+1 – расстояние от центра тяжести правой эпюры до правой опоры. Число уравнений моментов равно числу промежуточных опор. Совместное их решение позволяет найти неизвестные опорные моменты. Зная опорные моменты, рассматриваются отдельные пролеты и из уравнений статики находятся неизвестные опорные реакции. Если пролета всего два, то левый и правый моменты известны, т.к. это либо заданные моменты, либо они равны нулю. В результате получаем одно уравнение с одним неизвестным М1.

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Под

Сложное сопротивление

различные

сложным

сопротивлением понимают

комбинации простых напряженных состояний (растяжения,

I-я четв-ть

сжатия,

сдвига,

кручения,

изгиба).

общем

случае в

поперечных сечениях бруса действуют шесть компонентов

внутренних усилий: N, Qx, Qy, Mx, My, Mz=Mкр. Нормальная

сила

изгибающие

моменты

Mx,

вызывают

нормальные напряжения. От поперечных сил Qx, Qy и

крутящего

момента Mz=Mкр

возникают

касательные

напряжения. Знаки: N>0, если она

вызывает

растягивающие

напряжения.

My>0,

если они

вызывают растягивающие напряжения в точках положительной четверти осей координат (I-ая четверть). На рис. все>0.

Прямой изгиб не принято рассматривать как сложное сопротивление, хотя возникают два внутренних силовых фактора: изгибающий момент и поперечная сила. Сложный изгиб (неплоский изгиб), который вызывается нагрузками, расположенными в разных плоскостях, проходящих через ось балки. Изогнутая ось балки при этом не является плоской кривой. Косой изгиб — такой вид изгиба, когда все нагрузки действуют в одной плоскости, которая не проходят ни через одну из главных центральных осей инерции сечения. Косой изгиб приводят к двум плоским изгибам, раскладывая нагрузку в главных плоскостях zy и zx. В сечении возникают четыре компоненты внутренних усилий: Qx, Qy, Mx, и My. На основании принципа независимости действия сил полные нормальные напряжения равны сумме напряжений от раздельного действия Mx и My. Напряжение в произвольной точке с

координатами "x,y":	M	x	y	M y x		; Mx,My,x,y подставляются с учетом знака


	J			J
	J	x		J	y
		x			y

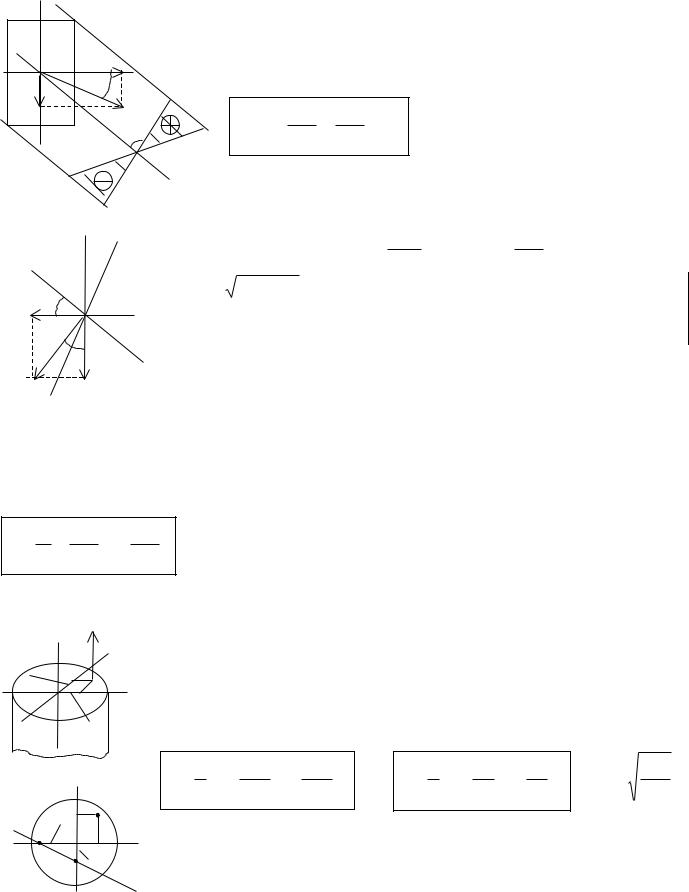
y	силовая
	линия
нейтраль-
ная линия

(Mx>0 и My>0,

четверти).

если

My , Mx

они вызывают растяжение в I-ой

Mx=M cos ; My=M sin , – угол

между "y" и плоскостью действия изгибающего момента М

(силовой

пл–стью).

M( y cos x sin )

Т.к.

на

J x

J y

нейтральной линии (оси) нормальные напряжения =0, то

уравнение нейтр. линии будет:

M y x 0

0 ,

x0, y0

– коорд. нейтр. линии, или

J x

J y

cos

sin

0 .

Это уравнение

прямой

линии,

проходящей

через

начало

координат. Ее положение определяется углом наклона к главной оси "х":

M y

если

Jx Jy,

то

нейтр.

линия

не

x 0

M x

J y

перпендикулярна к силовой линии. Нейтр. линия при косом изгибе повернута на

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

угол ( – ) от оси, перпендикулярной плоскости действия изгибающего момента, к

оси,

относительно которой момент инерции имеет минимальное значение (на рис.

это ось "y").

Наибольшие

напряжения

будут

точках

наиболее

удаленных от нейтральной линии: A и B. Для их

нахождения надо провести к контуру сечения

касательные параллельные нейтральной линии. Условие

max

прочности:

max

M y

[ ] ,

Wx=Jx/ymax;

Wy=Jy/xmax.

Для

н. л

хрупкого

материала

(чугун)

[ ]=[ p]

(допускаемое

min

напряжение на растяжение). Перемещение (прогиб) "f"

определяется геометрическим суммированием прогибов в

силовая

плоскостях xz и yz:

EJ x

d w

Mx ;

EJ y

d v

My .

линия

При

косом

изгибе

направление

полного

прогиба перпендикулярно к нейтральной линии и не

нейтр.

совпадает с направлением действующей нагрузки.

В случае неплоского

изгиба,

когда

нагрузки

не

лежат в

линия

одной плоскости, линия прогиба не перпендикулярна

нейтральной линии.

Изгиб с растяжением (внецентренное сжатие–растяжение).

Внецентренное растяжение–сжатие такой вид деформации, когда в поперечном

сечении жесткого стержня действуют продольная сила и изгибающий момент.

Нормальное напряжение в произвольной точке сечения с координатами "x,y" равно

сумме напряжений от продольной силы

изгибающих

моментов

Mx,

My:

M y

; знаки:

N>0 –

если

сила

растягивающая,

Mx, My>0,

если

моменты "растягивают" сечение в I-ой четверти. Внецентренное сжатие похоже на

косой

изгиб, только

добавляется

нормальная

сила.

На

практике

важен

случай

действия

одной

силы

(равнодействующей),

когда

она не

совпадает с осью балки и имеет координаты точки приложения

y I-ая

"xp,yp". Внутренние усилия: N=P; My=P xp; Mx=P yp. Координаты

четв.

"xp,yp" называются эксцентриситеты силы Р относительно

главных осей инерции

x,y. Точка приложения силы Р – полюс.

Напряжения:

x p F

yp F

или

x p

y) ,

J x,y

x,y

xр

i y

yн

yр

–радиусы

инерции

относительно

главных

центральных

осей

инерции

сечения.

Уравнение

нейтральной

линии,

на

которой

xн

н.л.

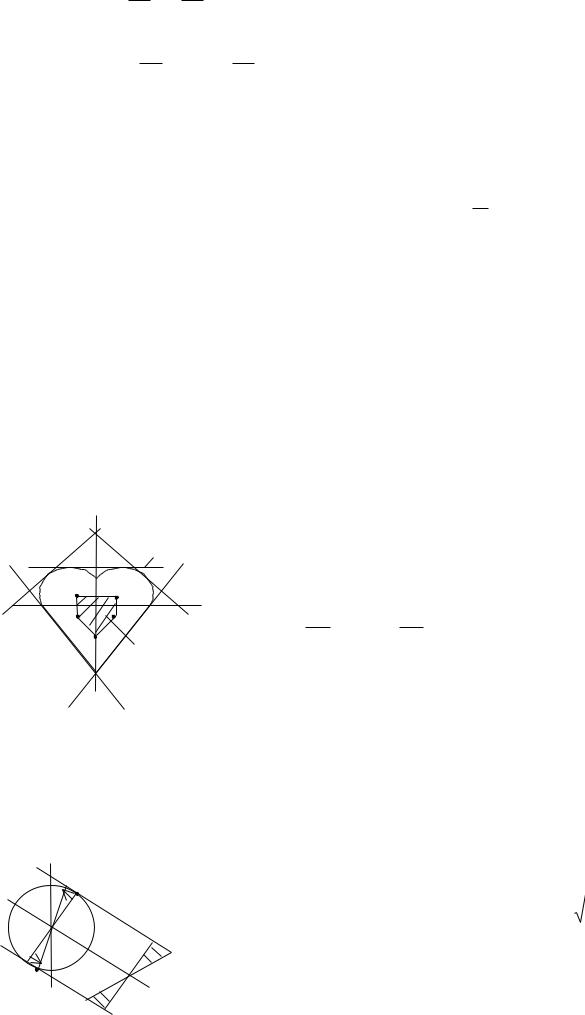
vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

=0, будет:

координат:

;



0 .

i2 x

Отрезки, отсекаемые нейтр. линией на осях

. Нейтральная линия и полюс (точка приложения

силы) лежат по разные стороны от начала координат.

Чем дальше от начала координат расположен полюс, тем ближе к центру сечения проходит нейтр. линия. Если полюс находится на одной из главных центральных осей инерции, то нейтр. линия перпендикулярна этой оси (например, если хр=0, т.е.

точка приложения силы Р находится на оси "y", то

		2
		i
x		y
x	H	0
	H

, нейтр. линия

параллельна оси "х", перпендикулярна оси "y"). Нейтр. линия может как пересекать сечение, так и проходить вне его, в этом случае во всем сечении напряжения будут одного знака: растягивающие или сжимающие. Это важно, например, при расчете кирпичных колон, которые плохо сопротивляются растяжению, и надо, чтобы они только сжимались. Когда сила Р приложена в центре тяжести сечения, то нейтр. линия находится в бесконечности. При перемещении силы Р от центра тяжести в сторону края сечения нейтр. линия перемещается из бесконечности к сечению, оставаясь параллельной самой себе. В какой-то момент она коснется сечения. При этом сила занимает предельное положение, при котором в сечении будут напряжения одного знака. Область вокруг центра тяжести сечения, внутри которой приложение силы Р вызывает в сечении напряжения одного знака, называется ядром сечения.

Чтобы получить очертание ядра сечения надо задать несколько положений нейтр.

линии, касательных к контуру сечения (нигде не

х =

пересекая его), определить отсекаемые ими отрезки на

координатных

осях

"хн,yн"

вычислить

соответствующие координаты точки приложения силы

x P

Р:

;

– координаты контура ядра

ядро

(на рис. n1n1– нейтр. линия, А1–соответствующая ей

точка ядра

сечения).

При многоугольной форме

контура сечения удобнее нейтр. линию совмещать с

каждой из сторон многоугольника. Для прямоугольного сечения – ядро сечения ромб, с диагоналями равными одной трети соответствующей стороны сечения, для круга – круг радиусом R/4, для двутавра – ромб.

Изгиб с кручением Совместное действие изгиба с кручением наиболее частый случай нагружения

валов. Возникают пять компонентов внутренних усилий: Qx, Qy, Mx, My, Mz=Mкр.

y		При расчете строят эпюры изгибающих Mx, My,	и крутящих
A		Mкр моментов и определяют опасное		сечение.

		Результирующий изгибающий момент M		M2	M2 .
		Результирующий изгибающий момент M		M2	M2 .
				x	y
		x
		x
	нейтр.
B	линия
B

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Макс.

нормальные и

касательные

напряжения в опасных

(A,B):

M2x M2y

max

кр

max

, (для

круга:

–осевой

момент сопротивления, Wр=

точках

R
3
2	–
2

полярный момент сопр-ния сечения).

Главные напряжения в наиболее опасных точках (А и В):

	1								0;		1	(
	1	( 2	4 2 );					2			1		2	4 2 ).
		( 2	4 2 );										2	4 2 ).
1	2									1	2
	2										2
Проверка прочности проводится по одной из теорий прочности:
IV-ая:	эквIV			2	3	2	[ ];			теория Мора: эквM					1 m	1 m	2	4
				2		2											2
															2	2
															2	2

где m=[ p]/[ c] – допуст. напр.растяжения/сжатия (для хрупких материалов –

Т.к. Wp=2 W, получаем: эквM	1	1 m	2	2	1 m	2	2	2
		[
	W		M x M y		2	Mкр M x M y ]
		2

2	[ ];

чугун).[ ];

эквIV	1	0,75M	2	2	2	В числителе – приведенный
	W		кр M x M y [ ];

принятой теории прочности. MпрM	1 m	2	2	1 m	2	2
	2	Mx My		2	Mкр Mx

момент по

M2 ] ; y

IV-ая: MпрIV	0,75M	2	2	2		0,75M	2
		кр Mx M y					кр

I-ая: MпрI

[

Mx My Mкр Mx

My ];

II-ая: MпрII

0,35 Mx M y

0,65 Mкр Mx

III-я: M

прIII

;

кр

или одной формулой: экв

пр

[ ], откуда

M	2	;

2 , при коэф.Пуасссона =0,3; y

момент сопротивления: W M пр ,

[ ]

диаметр вала: d 3 32Mпр . Формулы годятся и при расчете кольцевого сечения.

[ ]

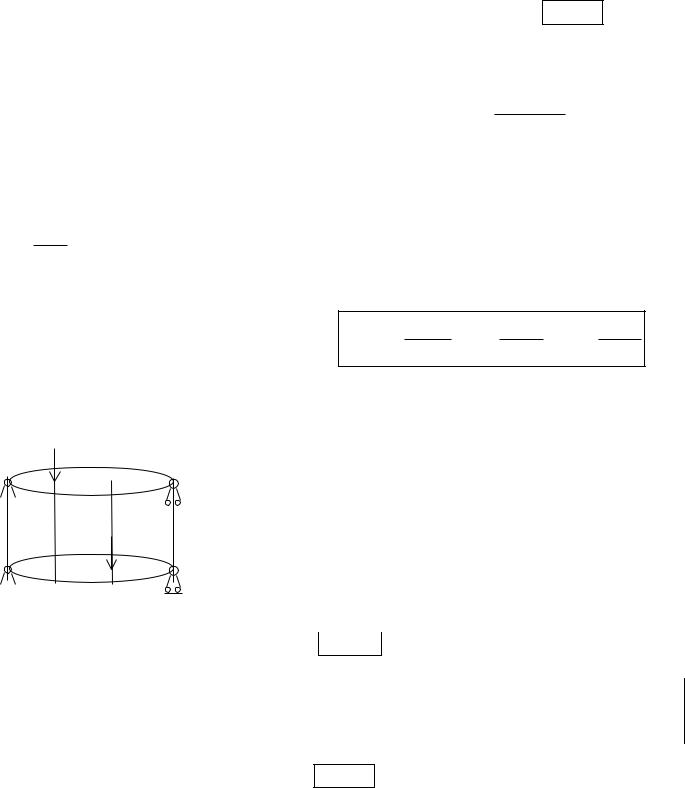
vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Общие методы определения перемещений Работа постоянных сил: А=Р Р, Р – обобщенная сила – любая нагрузка

(сосредоточенная сила, сосредоточенный момент, распределенная нагрузка), Р – обобщенное перемещение (прогиб, угол поворота). Обозначение mn означает перемещение по направлению обобщенной силы "m" , которое вызвано действием силы обобщенной "n". Полное перемещение, вызванное несколькими силовыми факторами: Р= РP+ РQ+ РM. Перемещения вызванные единичной силой или единичным моментом: – удельное перемещение. Если единичная сила Р=1 вызвала перемещение Р, то полное перемещение вызванное силой Р, будет: Р=Р Р. Если

силовые факторы, действующие на систему, обозначить Х1,Х2,Х3 и т.д., то перемещение по направлению каждого из них:

где Х1 11=+ 11; Х2 12=+ 12; Хi mi=+ mi. Размерность

1=Х1 11+Х2 12+Х3 13+…

Дж

2=Х1 21+Х2 22+Х3 23+…

удельных перемещений:

[ ]

, Джджоули

3=Х1 31+Х2 32+Х3 33+…

][X

]

размерность работы 1Дж = 1Нм.

Работа внешних сил, дейст-щих на упругую систему: A Pd P PPdP

– действительная работа при статическом действии обобщенной силы на

упругую систему равна половине произведения окончательного значения силы на окончательное значение соответствующего перемещения. Работа внутренних сил

(сил упругости) в случае плоского изгиба:

L	2	dx	L	2	dx
A	M			N
	2EJ			2EF
0			0

L	2	dx
k	Q	dx
k	2GF
0	2GF
0

k – коэффициент, учитывающий неравномерность распределения касательных напряжений по площади поперечного сечения, зависит от формы сечения.

На основании закона сохранения энергии: потенциальная энергия U=A. Теорема о взаимности работ (теорема Бетли). Два состояния упругой ситемы:


	Р1			11– перемещение по направл. силы Р1	от действия силы Р1;
				12– перемещение по направл. силы Р1	от действия силы Р2;
	11	21		12– перемещение по направл. силы Р1	от действия силы Р2;
	первое состояние			21– перемещение по направл. силы Р2	от действия силы Р1;


				22– перемещение по направл. силы Р2	от действия силы Р2.
		Р2		А12=Р1 12 – работа силы Р1 первого состояния на
				А12=Р1 12 – работа силы Р1 первого состояния на
	12	22		перемещении по ее направлению, вызванном силой Р2
				перемещении по ее направлению, вызванном силой Р2
	второе состояние			второго состояния. Аналогично: А21=Р2 21 – работа силы
				Р2 второго состояния на перемещении по ее направлению,

вызванном силой Р1			первого состояния. А12=А21. Такой же результат получается при

любом числе сил и моментов. Теорема о взаимности работ: Р1 12=Р2 21. Работа сил первого состояния на перемещениях по их направлениям, вызванных

силами второго состояния, равна работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния.

Теорема о взаимности перемещений (теорема Максвелла) Если Р1=1 и Р2=1, то Р1 12=Р2 21, т.е. 12= 21, в общем случае mn= nm.

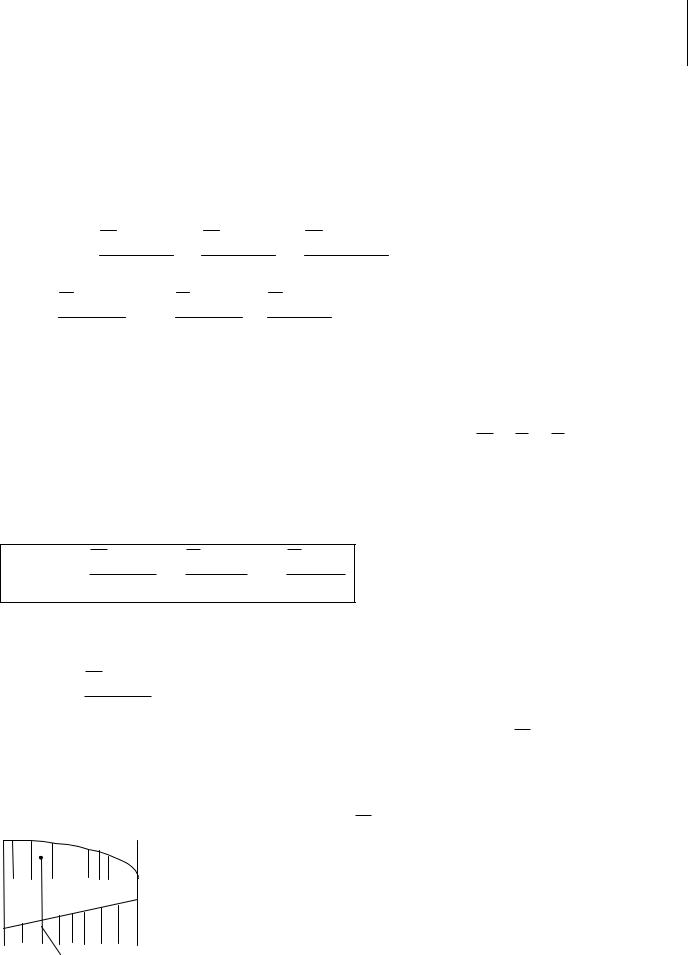
vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй единичной силы, вызванному первой силой. Универсальный метод определения перемещений (линейных и углов поворота) – метод Мора. К системе прикладывают единичную обобщенную силу в точке, для которой ищется обобщенное перемещение. Если определяется прогиб, то единичная сила представляет собой безразмерную сосредоточенную силу, если определяется угол поворота, то – безразмерный единичный момент. В случае пространственной системы действуют шесть компонентов внутренних усилий. Обобщенное перемещение определяется формулой (формула или интеграл Мора):

Черта над М, Q и N

L M

кр

указывает на то, что эти

[

внутренние усилия вызваны

L Q

L N

действием единичной силы.

]

Для вычисления входящих в

формулу интегралов надо

перемножить эпюры

соответствующих усилий. Порядок определения перемещения: 1) для заданной

(действительной или грузовой) системы находят выражения Mn, Nn и Qn; 2) по направлению искомого перемещения прикладывают соответствующую ему единичную силу (силу или момент); 3) определяют усилия Mm ; Nm ; Qm от действия единичной силы; 4) найденные выражения подставляют в интеграл Мора и интегрируют по заданным участкам. Если полученное mn>0, то перемещение совпадает с выбранным направлением единичной силы, если <0, то противоположно. Для плоской конструкции:

L M		M	ds	L
[	i	p
		EJ
0				0

N	N	ds
i	p
	EF

Q	Q	ds
i	p	]
		]
GF

. Обычно при определении

перемещений пренебрегают влиянием продольных деформаций и сдвигом, которые вызываются продольной N и поперечной Q силами, учитываются только перемещения, вызываемые изгибом. Для плоской системы будет:

	L M		M	ds
		i	p		.
mn			EJ
mn
	0
	0

Вычисление интеграла Мора способом Верещагина. Интеграл

Mi Mpdz

для случая,

когда эпюра от заданной нагрузки имеет произвольное очертание, а от единичной – прямолинейное удобно определять графо-аналитическим способом, предложенным

Верещагиным.

dz y

, где – площадь

Эпюра Мр

эпюры Мр от внешней нагрузки, yc– ордината эпюры от

единичной нагрузки под центром тяжести эпюры Мр.

Результат перемножения эпюр равен произведению

Эпюра

площади одной из эпюр на ординату другой эпюры,

M i

взятой под центром тяжести площади первой эпюры.

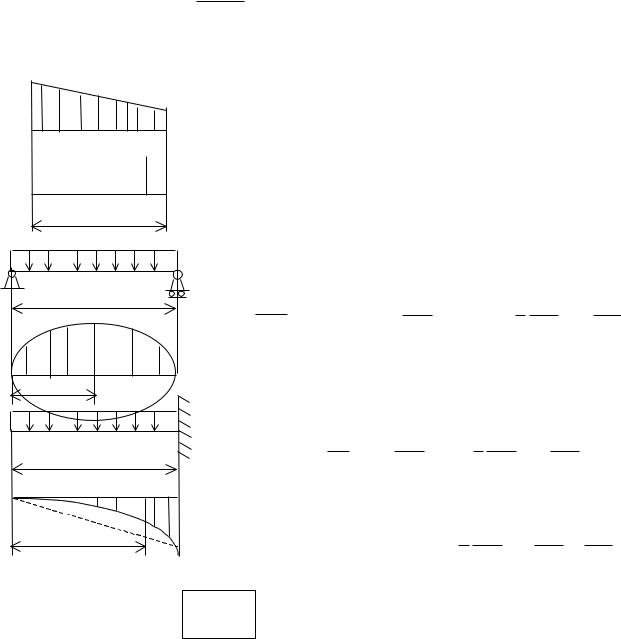
vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Ордината должна быть обязательно взята из прямолинейной эпюры. Если обе эпюры прямолинейны, то ординату можно взять из любой.

Перемещение:		y	C	. Вычисление по этой формуле производится по
	iP		C
	iP	EJ
		EJ

участкам, на каждом из которых прямолинейная эпюра должна быть без переломов. Сложную эпюру Мр разбивают на простые геометрические фигуры, для которых

		легче определить координаты центров тяжести. При
a		перемножении двух эпюр, имеющих вид трапеций, удобно
	b	использовать формулу: y			L	(2ac 2bd ad bc) . Эта же
					L
			C
			C	6
				6

L q

x	=L/2
c	q
	q

d	формула годится и для треугольных эпюр, если подставить
	соответствующую ординату = 0.

При действии равномерно распределенной нагрузки на шарнирно опертую балку эпюра строится в виде выпуклой квадратичной параболы, площадь которой

2hL		2			2		3
	(для рис. h	qL	, т.е.	2 qL		L	qL	,
3		8		3	8		12

хС=L/2).

Для "глухой" заделки при равномерно распределенной нагрузке имеем вогнутую квадратичную параболу, для

					hL		2					2				3
				которой	hL	; h	qL	,		1 qL			L		qL		, хС=3L/4.
		L		которой	3	; h	2	,		3	2		L		6		, хС=3L/4.
					3		2			3	2				6

			M	Тоже можно получить, если эпюру представить
			M
			p	разностью площади треугольника и площади выпуклой


			h								2				3		3
			h						1 qL			L		qL			qL
x	c			квадратичной параболы:					1 qL			L		qL			qL	.
	c
									2	2				12			6

"Отсутствующая" площадь считается отрицательной.

Теорема Кастильяно. P U – перемещение точки приложения обобщенной силы

по направлению ее действия равно частной производной от потенциальной энергии по этой силе. Пренебрегая влиянием на перемещение осевых и поперечных сил,

L M2dx				M(s)ds M(s)
имеем потенциальную энергию: U		, откуда	P		P	.
	2EJ			EJ
0			S

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Статически неопределимые системы Статически неопределимые системы – системы, силовые факторы в элементах

которых не могут быть определены только из уравнений равновесия твердого тела. В таких системах число связей больше, чем необходимо для равновесия. Степень статической неопределимости: S = 3n – m, n – число замкнутых контуров в конструкции, m – число одиночных шарниров (шарнир, соединяющий два стержня, считается за один, соединяющий три стержня – за два и т.д.). Метод сил – в качестве неизвестных принимают силовые факторы. Последовательность расчета: 1) устанавливают степень статич. неопределимости; 2) путем удаления лишних связей заменяют исходную систему статически определимой – основной системой (таких систем может быть несколько, но при удалении лишних связей не должна нарушаться геометрическая неизменяемость конструкции); 3) основную систему загружают заданными силами и лишними неизвестными; 4) неизвестные усилия должны быть подобраны так, чтобы деформации исходной и основной систем не отличались. Т.е. реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям = 0. Канонические уравнения метода сил:

		Эти уравнения являются дополнительными ур-ями
	11Х1+ 12Х2+…+ 1nХn+ 1p=0
		деформаций, которые позволяют раскрыть статич.
	21Х1+ 22Х2+ + 2nХn+ 2p=0
		неопределимость. Число ур-ий = числу
	. . . . . . . . . . . .
		отброшенных связей, т.е. степени
	n1Х1+ n2Х2+ + nnХn+ np=0
		неопределимости системы.

ik – перемещение по направлению i, вызванное единичной силой действующей по направлению k. ii – главные, ik – побочные перемещения. По теореме о взаимности перемещений: ik= ki. ip– перемещение по направлению связи i, вызванное действием заданной нагрузки (грузовые члены). Перемещения, входящие в канонические уравнения удобно определять по методу Мора. Для этого к основной системе прикладывают единичные нагрузки Х1=1, Х2=1, Хn=1, внешнюю нагрузку и строят эпюры изгибающих моментов. По интегралу Мора находят:

M M	p	ds
1	p
EJ

;

M	M	p	ds
2		p
	EJ

; ….;

M	M	p	ds
n		p
	EJ

;

M M ds
1	1
EJ

;

M	M	ds
2	2
	EJ

; ….;

M	M	ds
n	n
	EJ

;

M M	2	ds
1	2
EJ

;

M M	3	ds
1	3
EJ

; ….;

M	M	ds
i	k
	EJ

. Черта над М

указывает на то, что эти внутренние усилия вызваны действием единичной силы. Для систем, состоящих из прямолинейных элементов перемножение эпюр удобно

производить по способу Верещагина.

	P	y	Cp
	P		Cp
1P	EJ
1P

;		1 yC1	и т.д. Р –

	11	EJ

площадь эпюры Мр от внешней нагрузки, yСр– ордината эпюры от единичной нагрузки под центром тяжести эпюры Мр, 1 – площадь эпюры М1 от единичной нагрузки. Результат перемножения эпюр равен произведению площади одной из

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

эпюр на ординату другой эпюры, взятой под центром тяжести площади первой эпюры.

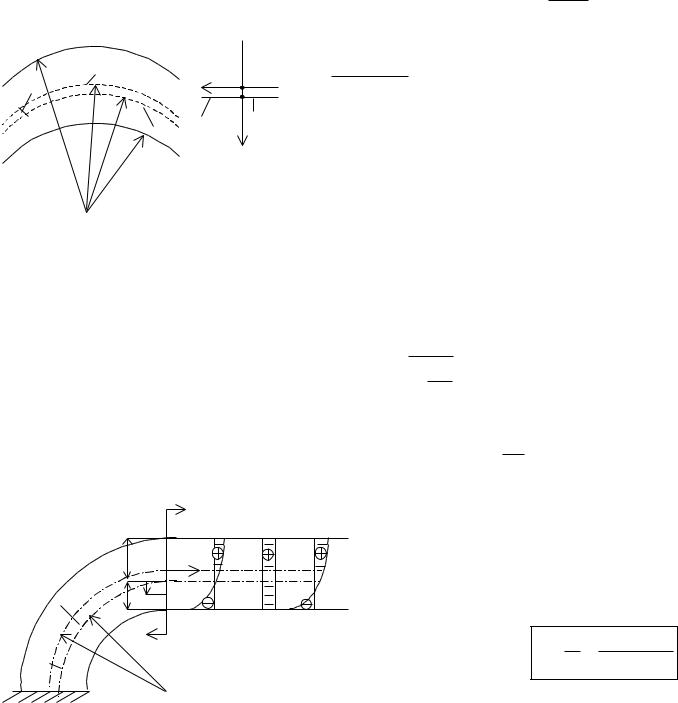
vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Расчет плоских кривых брусьев (стержней)

К кривым брусьям относятся крюки, звенья цепей, арки и т.п. Ограничения: поперечное сечение имеет ось симметрии, ось бруса плоская кривая, нагрузка действует в той же плоскости. Различают брусья малой кривизны: h/R<1/5, большой кривизны: h/R 1/5. При изгибе брусьев малой кривизны нормальные напряжения

рассчитывают по формуле Навье, как для балок с прямой осью:

M y J x

. При

		.ось бруса	x	С
e			x		e



	R			0	y
	R
			нейтр.ось
		r
R		Н		y
R
2
		R
		1
	O

чистом изгибе брусьев большой кривизны:

M y		,
eF(r	y)


н

rН– радиус нейтрального слоя, е=R – rН, R – радиус слоя, в котором расположены центры тяжести сечения. Нейтральная ось кривого бруса не проходит через центр тяжести сечения С. Она всегда расположена ближе к центру кривизны, чем центр тяжести сечения.

r		F	, =rН – y. Зная радиус нейтрального слоя можно определить расстояние

Н		dF


	F

"е" от нейтрального слоя до центра тяжести. Для прямоугольного сечения высотой

h, с наружным радиусом R2 и внутренним R1:

r		h
r
Н		R
	ln	R
	ln	R
		R

2 1

; для разных сечений

формулы приведены в справочной лит-ре. При h/R<1/2 независимо от формы

сечения можно определять "е" по приближенной формуле:

Jx RF

где Jx – момент

инерции сечения относительно оси, проходящей через его центр тяжести

		М			перпендикулярно плоскости кривизны
		М	M	N	бруса. Нормальные напряжения в
			M	N	бруса. Нормальные напряжения в
	h2	N			сечении распределяются по
	h2	N			гиперболическому закону (у наружного
					гиперболическому закону (у наружного
нейтр.ось	h1	y			края сечения меньше, у внутреннего
нейтр.ось	h1				края сечения меньше, у внутреннего
					больше). При действии еще и
е		rН			нормальной силы N: N	M y
е	R				F	eF(rн y)
	R				F	eF(rн y)
					(здесь rН – радиус нейтрального слоя,
					который был бы при действии только

момента М, т.е. при N=0, но в действительности при наличии продольной силы этот

слой уже не является нейтральным). Условие прочности:		N	M y	[ ] ,
	max	F	eF(rн y)

при этом рассматриваются крайние точки, в которых суммарные напряжения от

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

изгиба и растяжения–сжатия будут наибольшие, т.е. y= – h2 или y= h1. Перемещения удобно определять методом Мора.

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

Устойчивость сжатых стержней. Продольный изгиб

Разрушение стержня может произойти не только потому, что будет нарушена

прочность, но и оттого, что стержень не сохранит заданной формы. Например, изгиб

при продольном сжатии тонкой линейки. Потеря устойчивости прямолинейной

формы равновесия центрально сжатого стержня называется продольным изгибом.

Упругое равновесие устойчиво, если деформированное тело при любом малом

отклонении от состояния равновесия стремится вернуться к первоначальному

состоянию и возвращается к нему при удалении внешнего воздействия.

Нагрузка, превышение которой вызывает потерю устойчивости,

называется критической нагрузкой Ркр (критической силой). Допускаема

нагрузка [P]=Pкр/nу, nу – нормативный коэффициент запаса устойчивости.

Приближенное дифференциальное ур-ние упругой линии:

d2 y

M(x) , Е –модуль упругости материала стержня, М –

EJ min

dx2

изгибающий момент, Jmin– наименьший момент инерции сечения

стержня. При потере устойчивости прогиб, как правило, происходит

перпендикулярно к оси наименьшей жесткости, относительно которой —

J=Jmin. Рассматривается приближенное дифф-ное ур-ие, т.к. потеря устойчивости

возникает при малых деформациях. M=—Py, получаем однородное дифф-ное

уравнение:

y 0 , где k

. Решая дифф-ное ур-ие находим

min

наименьшее значение критической силы – формула Эйлера:

min

–

кр

формула дает значение критической силы для стержня с шарнирно закрепленными

концами. При различных закреплениях:

P	2	EJ
	2
			min
			min
кр		2
	L

, – коэффициент приведения

длины. При шарнирном закреплении обоих концов стержня =1; для стержня с заделанными концами =0,5; для стержня с одним заделанным и другим свободным концом =2; для стержня с одним заделанным и другим шарнирно закрепленным концом =0,7.

Критическое сжимающее напр-ние.:

кр

Pкр

2 E

– гибкость стержня,

min

imin

Jmin

– наименьший главный радиус инерции площади сечения стержня. Эти

формулы справедливы только тогда, когда напряжения кр пц– предел

пропорциональности, т.е. в пределах применимости закона Гука. Формула Эйлера

применима при гибкости стержня:		2 E	, например, для стали Ст3 (С235)
применима при гибкости стержня:	кр	пц	, например, для стали Ст3 (С235)
	кр

кр 100. Для случая < кр критическое напряжение вычисляется по эмпирической

vk.com/club152685050 | vk.com/id446425943

http//:www.svkspb.nm.ru

(полученной экспериментально) формуле Ясинского: кр= a — b , коэффициенты "a" и "b" в справочной лит-ре (Ст3: a=310МПа; b=1,14МПа).

Достаточно короткие стержни, для которых < 0=40 (для сталей) назыв-тся стержни малой гибкости. Такие стержни рассчитывают только на прочность, т.е. принимаюткр= т (предел текучести) – для пластичных материалов и кр= В (временное сопротивление) – для хрупких материалов. При расчете стержней большой гибкости

используют условие устойчивости:

		P
		F
		F
		брутто

[ у

]

Fбрутто– полная площадь

сечения,

(Fнетто=Fбрутто—Fослабл –площадь ослабленного сечения с учетом площади отверстий в сечении Fослабл, например, от заклепок). [ у]= кр/nу, nу– нормативный коэф. запаса устойчивости. Допускаемое напряжение [ у] выражается через основное допускаемое напряжение [ ], используемое при расчетах на прочность: [ у]= [ ],

– коэффициент уменьшения допускаемого напряжения для сжатых стержней (коэффициент продольного изгиба). Значения приведены в табл. в учебниках и зависят от материала стержня и его гибкости (например, для стали Ст3 при =120

=0,45).

При проектировочном расчете требуемой площади сечения на первом шаге

принимают 1=0,5–0,6; находят:

F
брутто

P[ ]

. Далее зная Fбрутто, подбирают

сечение, определяют Jmin, imin и , устанавливают по табл. фактическое 1I, если оно существенно отличается от 1, расчет повторяется при среднем 2= ( 1+ 1I)/2. В результате второй попытки находят 2I, сравнивают с предыдущем значением и т.д., пока не достигнуто достаточно близкое совпадение. Обычно требуется 2-3 попытки.

vk.com/club152685050 | vk.com/id446425943

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете Сопротивление материалов

#
12.08.201920.41 Mб38Лекции Сопротивление материалов.pdf
#
15.08.20196.15 Mб20формула Ясинского.pdf