
vk.com/club152685050 | vk.com/id446425943
http//:www.svkspb.nm.ru |
11 |
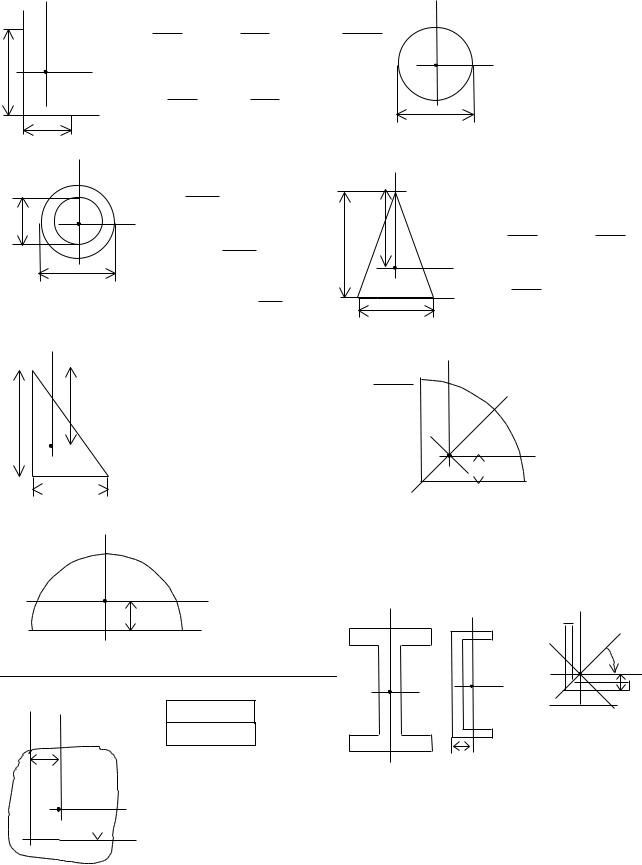
Моменты инерции сечений простой формы |
|
Прямоугольное сечение |
Круг |
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
bh |
|
|
|
|
|
|
|
|
|
hb |
|
|
|
|
|
|
|
|
|
|
b h |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
|
; |
J |
|
|
|
|
|
; |
|
J |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
3 |
|
|
y |
|
|
3 |
|
|
x y |
|
4 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
h |
|
|
|
|
С |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bh |
3 |
|
|
|
|
|
|
hb |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
; |
|
J |
|
|
|
; |
J |
|
|
|
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
xy |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Кольцо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
H |
(1 c |
4 |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d |
в |
|
|
|
|
С |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2/3h |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
J |
|
|
|
|
|
H |
|
(1 c |
4 |
) |
|
|
h |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
64 |
|
|
|
|
|
|
|
|
|
С |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
d |
н |
|
|
|
|
|
|
|
|
0; |
|
|
|
c |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Прямоугольный |
|
xy |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
треугольник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
b |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
bh3 |
|
|
|
|
|
|
|
|
hb3 |
|
|
|
|
|
b2 h 2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
J |
x |
|
|
; J |
y |
|
|
; J |
xy |
; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
2/3h |
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
72 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
h |
С |
|
|
|
x |
J xy |
|
0, если гипотенуза" убывает" |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bh3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x1 на рис.(-). |
|
|
J x |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
Полукруг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y |
|
|
|
r |
4 |
|
d |
4 |
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
J |
p |
|
|
2 |
|
|
32 |
|
|
||
|
|
|
|
|
|
|
|
|||||
С |
x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
r |
4 |
|
d |
4 |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
J |
x |
J |
y |
|
|
4 |
|
|
64 |
||
|
|
|
|
|
|
|
|
|||||
|
J |
|
0 |
|
|
|
|
|||||
d |
xy |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Треугольник
равнобедренный
x
x1
y
y0 С
|
|
|
bh |
3 |
|
|
J |
|
|
|
|
; |
|
x |
36 |
|
||||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
bh |
3 |
|
|
J |
|
|
|
|
||
x |
|
|
|
|
||
|
1 |
12 |
|
|||
|
|
|
||||
|
|
|
|
|
|
|
x0
x  0,424R
0,424R
|
|
|
hb |
3 |
|
|
|
|
|
J |
|
|
|
; |
J |
|
0 |
||
y |
48 |
xy |
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
Четверть круга
Jy=Jx=0,055R4
Jxy= 0,0165R4
на рис. (—)
Jx0=0,0714R4 Jy0=0,0384R4
|
y |
|
|
|
J |
|
|
0,11 R 4 |
; |
||||
|
|
|
|
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
J |
|
|
J |
|
|
|
R 4 |
||
|
С |
|
x |
y |
|
x |
1 |
8 |
; |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,424R |
x1 |
J xy |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
Моменты |
инерции |
|
|
относительно |
|||||||||
параллельных осей: |
|
|
|
|
|
|
|
|
|
|
|
||
y1 |
y |
Jx1=Jx + a2F; |
|
|
|
|
|
||||||
Jy1=Jy + b2F; |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
Моменты |
инерции |
|
|
стандартных |
|||||||
профилей |
находятся |
|
|
из |
|
таблиц |
|||||
сортамента: |
|
|
|
|
|
|
|
|
|
||
Двутавр |
Швеллер |
|
Уголок |
|
|
||||||
|
y |
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=—45 |
о |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
C |
|
|
|
|
|
C |
|
x |
|
|
|
x |
|
|
|
|
|
|
|
||
C |
x |
|
|
J |
|
J |
|
z0 |
|
||
|
|
|
|
x0 |
y0 |
|
|||||
|
|
|
J |
|
|
sin 2 |
|||||
|
|
|
|
|
|
||||||
|
|
|
xy |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
С x a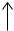 x1
x1
момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат
расстояния между осями. |
Jy1x1=Jyx + abF; |
("a" и "b" |
подставляют в формулу с учетом их знака).
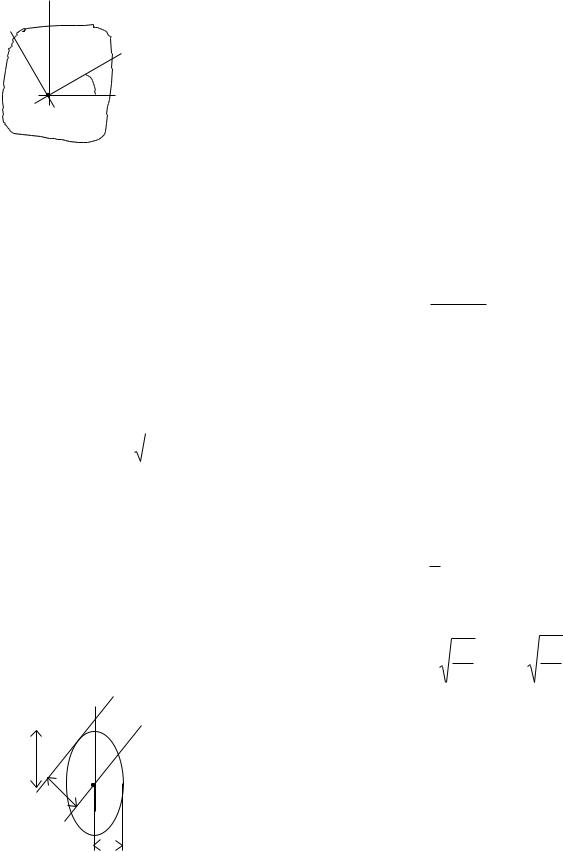
vk.com/club152685050 | vk.com/id446425943
http//:www.svkspb.nm.ru |
12 |
|
y |
|
Зависимость между моментами инерции при повороте осей: |
|||||||
y |
|
|
|
2 |
|
2 |
2 |
2 |
||
1 |
|
|
Jx1=Jxcos |
+ Jysin — Jxysin2 ; |
Jy1=Jycos |
+ Jxsin + Jxysin2 ; |
||||
|
|
x |
|
1 |
(Jx — Jy)sin2 + Jxycos2 ; |
|
||||
|
|
1 |
Jx1y1= |
|
||||||
С |
|
x |
2 |
|
||||||
|
|
|
|
|
|
|||||
Угол |
>0, если переход от старой системы координат к новой |
|||||||||
|
|
|||||||||
|
a |
|
||||||||
|
|
происходит против час.стр. Jy1 |
+ Jx1= Jy + Jx |
|||||||
|
|
|
||||||||
|
|
|
Экстремальные |
(максимальное |
и минимальное) значения |
|||||
моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол,
|
|
|
|
2 J |
|
|
|
||
определяющий положение главных осей: |
tg2 |
|
|
|
|
xy |
|
, если 0>0 |
оси |
0 |
J |
|
J |
|
|||||
|
|
|
|
||||||
|
|
|
|
y |
x |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:
|
|
|
J x J y |
|
1 |
|
|
|
|
|
|
|
|
J |
max |
|
|
|
(J |
x |
J |
y |
)2 |
4 J2 |
|
||
|
|
|
|
||||||||||
|
|
2 |
|
2 |
|
|
|
|
xy |
|
|||
|
min |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jmax + Jmin= Jx + Jy. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:
Jx1=Jmaxcos2 + Jminsin2 ; |
Jy1=Jmaxcos2 + Jminsin2 ; Jx1y1= |
1 |
(Jmax — Jmin)sin2 ; |
|
2 |
||||
|
|
|
Конечной целью вычисления геометрических характеристик сечения является определение главных центральных моментов инерции и положения главных
центральных осей инерции. Радиус инерции — |
i |
|
|
J |
x |
; |
i |
|
|
J y |
|
; |
|
2 |
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x |
|
F |
|
|
y |
|
F |
|
Jx=F ix |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Jy=F iy2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
x1 |
Если Jx |
и Jy главные моменты инерции, то |
|
ix и iy — |
||||||||||||||
|
|
|
|
|
|
главные радиусы инерции. Эллипс, построенный на главных |
|||||||||||||||||||
|
ix |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
С |
|
|
|
радиусах инерции как на полуосях, называется эллипсом |
|||||||||||||||||||
|
|
|
|
|
инерции. При помощи эллипса инерции можно графически |
||||||||||||||||||||
|
ix1 |
x |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
найти радиус инерции ix1 |
для любой оси х1. Для этого надо |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
провести касательную к эллипсу, параллельную оси |
х1, и |
||||||||||||||||
|
|
|
|
|
|
|
|
измерить |
расстояние от |
этой |
оси |
|
до |
касательной. |
Зная |
||||||||||
|
|
|
|
iy |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
радиус инерции, можно найти момент инерции сечения |
|||||||||||||||||
относительно оси х1: J x |
F i2x . Для сечений, имеющих более двух осей симметрии |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех
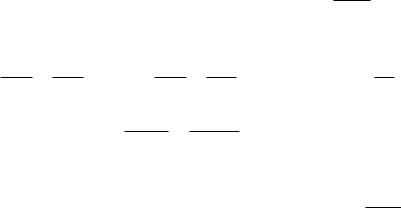
vk.com/club152685050 | vk.com/id446425943
http//:www.svkspb.nm.ru |
13 |
центральных осей равны между собой, Jxy=0, эллипс инерции обращается в круг инерции.
Моменты сопротивления.
Осевой момент сопротивления — отношение момента инерции относительно оси к
|
|
|
J |
|
|
|
W |
x |
3 |
3 |
|
расстоянию от нее до наиболее удаленной точки сечения. |
|
[см , м ] |
|||
x |
|
y |
|||
|
|
|
|
|
|
|
|
|
max |
|
|
Особенно важны моменты сопротивления относительно главных центральных осей:
|
|
|
|
J |
|
|
bh |
2 |
|
|
|
|
J |
y |
|
b |
2 |
h |
|
|
|
|
|
|
|
J |
|
|
|
R |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
прямоугольник: Wx |
x |
|
; |
Wy |
|
|
|
|
|
|
; круг: Wx=Wy= |
x |
|
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
h / 2 |
6 |
|
b / 2 |
6 |
R |
4 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
d |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
трубчатое сечение (кольцо): Wx=Wy= |
x |
|
|
H |
(1 |
4 |
) , где = dН/dB. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d |
H |
|
/ 2 |
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полярный момент |
сопротивления |
— отношение |
полярного |
момента |
инерции к |
|||||||||||||||||||||||||||
расстоянию от полюса до наиболее удаленной точки сечения: |
W |
|
|
J |
p |
|
. |
|
|
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
p |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для круга Wр= |
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vk.com/club152685050 | vk.com/id446425943
http//:www.svkspb.nm.ru |
14 |
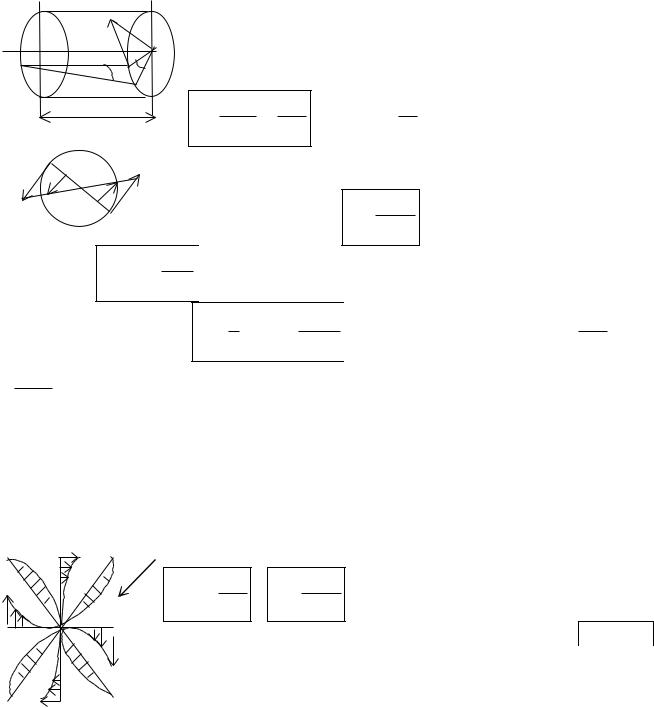
Кручение Такой вид деформации, при котором в поперечных сечениях возникает только одни
крутящие моменты — Мк. Знак крутящего момента Мк удобно определять по направлению внешнего момента. Если при взгляде со стороны сечения внешний момент направлен против час.стр., то Мк>0 (встречается и обратное правило). При кручении происходит поворот одного сечения относительно другого на угол закручивания - . При кручении круглого бруса (вала) возникает напряженное состояние чистого сдвига (нормальные напряжения отсутствуют), возникают только
|
|
|
касательные напряжения. Принимается, что сечения плоские |
|
|
|
|
до закручивания остаются плоскими и после закручивания — |
|
|
|
закон плоских сечений. Касательные напряжения в точках |
||
|
|
|
||
|
|
|
сечения изменяются пропорционально расстоянию точек от |
|
|
оси. Из закона Гука при сдвиге: = G, G — модуль сдвига, |
|||
|
|
|||
|
|
|
L
|
M |
|
M |
|
|
|
k |
|
k |
||
|
|
|
|
||
|
J |
p |
|
W |
|
|
|
|
|
p |
|
,
|
|
J |
W |
|
p |
|
||
p |
|
R |
|
|
— полярный момент
кручении.
max
L
сопротивления круглого сечения. Касательные напряжения в центре равны нулю, чем дальше от центра, тем они больше.
Угол закручивания Mk L , GJp — жесткость сечения при
GJp
M |
|
|
k |
— относительный угол закручивания. Потенциальная |
|
GJ |
||
|
||
p |
|
энергия при кручении: |
U |
1 |
M |
|
|
|
2 |
k |
|||||
|
|
|
||||
|
|
|
|
|
= [nпр ед] , для пластичного материала
|
|
2 |
|
|
|
|
|
|
|
|
|
|
M |
L |
|
max |
M |
k |
[ ] |
, [ ] |
|||
k |
. Условие прочности: |
||||||||||
|
|
|
|
||||||||
2GJ |
|
W |
|||||||||
|
p |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
за пред принимается предел текучести при сдвиге
т, для хрупкого материала – в прочности. Условие жесткости закручивания.
– предел прочности, [n] – коэффициент запаса при кручении: max [ ] – допустимый угол
Кручение бруса прямоугольного сечения При этом нарушается закон плоских сечений, сечения некруглой формы при кручении искривляются – депланация поперечного сечения.
Эпюры касательных напряжений прямоугольного сечения.
|
|
|
M |
k |
|
|
|||
|
|
|
|
|
|
max |
|
W |
|
|
|
|
||
|
|
|
|
k |
;
M |
L |
k |
|
GJ |
|
|
k |
, Jk и Wk — условно называют моментом
инерции и моментом сопротивления при кручении. Wk= hb2,
max |
|
|
|
||
Jk= hb3 |
, |
Максимальные касательные напряжения max будут |
|||
|
посредине длинной стороны, напряжения по середине короткой |
||||
|
стороны: |
= |
max, |
коэффициенты: , , приводятся в |
|
справочниках в зависимости от отношения h/b (например, при h/b=2, =0,246; =0,229; =0,795.
