Цифры и числа

Система счисления - это способ записи чисел при помощи письменных знаков. Системы счисления бывают позиционные, непозиционные и смешанные.

Позиционные системы счисления

Цифры и основание системы счисления

В позиционных системах счисления для записи чисел используются числовые знаки, они же - цифры.

Всем привычная десятичная система счисления - позиционная. Двоичная, восьмеричная, шестнадцатеричная системы счисления - это тоже позиционные системы счисления.

Позиционные системы счисления различаются между собой количеством используемых в них цифр. Например, в десятичной системе счисления используется десять цифр от 0 до 9. Собственно, система счисления называется десятичной потому, что в ней используется десять цифр. В двоичной - как следует из названия - используется только две цифры - это 0 и 1. В восьмеричной - восемь цифр от 0 до 7. Количество используемых в системе счисления цифр называется основанием системы счисления.

Если основание системы счисления больше 10, то обычно используют буквы латинского алфавита, начиная с A. Так, в шестнадцатеричной системе счисления для записи чисел используются десятичные цифры от 0 до 9 (10 символов) и буквы от А до F (плюс ещё 6 недостающих символов) - всего шестнадцать разных цифр. Когда буквы используются при записи числа, то они тоже называются цифрами - например, цифра “A”.

Обычно из контекста понятно, в какой системе счисления записано число. Например, если Вы читаете новости на каком-нибудь сайте, и там написано, что «учёные установили, что длина экватора Земли равна примерно 40075.7 км», то Вам врядли покажется, что это число в восьмеричной или в шестнадцатеричной системе счисления. Обычно все числа записываются в десятичной системе счисления - и в данном случае по умолчанию считается, что число тоже записано в десятичной системе счисления.

Но в некоторых случаях, чаще всего, когда используются числа в разных системах счисления, важно знать, в какой системе счисления записано это число. Чтобы отличать основания систем счисления, это основание записывается как нижний индекс после числа. Например “40075.7₁₀” - означает явно, что это число записано в десятичной системе счисления. Если бы было записано так: “40075.7₈”, то это число следовало бы интерпретировать как число в восьмеричной системе счисления.

Десятичная система счисления

Одна и та же цифра в позиционной системе счисления имеет разное значение в зависимости от того, где эта цифра находится в числе.

Например, число 175.3₁₀ в десятичной системе счисления содержит в себе четыре цифры - 1, 7, 5 и 3. В этом числе 3 - это десятые доли, 5 - это количество единиц, 7 - это количество десятков, а 1 - это количество сотен. Если перед единицей дописать ещё цифру, то это будут уже тысячи.

Значение, которое добавляет цифра в десятичной системе счисления во всё число, определяется по формуле: 10^{позиция}. Позиции нумеруются начиная с нуля, причём цифра, стоящая непосредственно перед десятичной точкой, всегда считается нулевой позицией. Влево номер позиции увеличивается, а вправо - уменьшается.

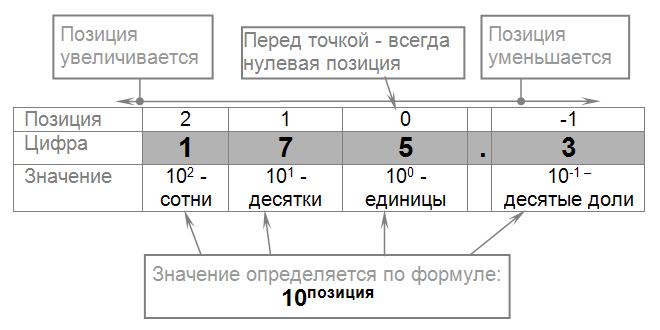
Перемножив и сложив, мы получим, собственно само число: 1*100+7*10+5+3/10=175.3₁₀.

Эта формула справедлива для абсолютно любых позиционных систем счисления, только в каждой системе счисления вместо 10 подставляется своё основание.

Восьмеричная система счисления

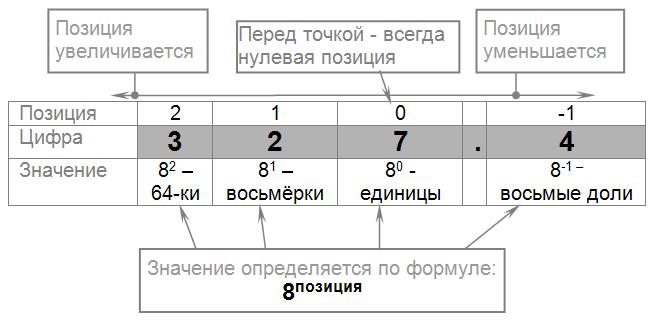
Например, в восьмеричной системе счисления число 327.4₈ - означает 3 64-ки, 2 восьмёрки, 7 единиц и 4 восьмых долей (то есть, в десятичной это было бы число 64*3+2*8+7+4/8=219.5₁₀):

Двоичная система счисления

Пример для числа 101.11₂ в двоичной системе счисления:

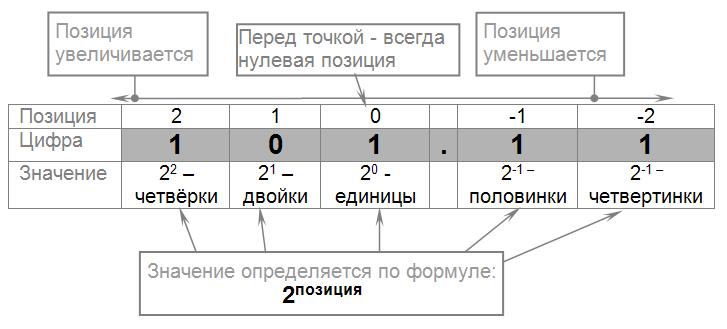
Число 101.11₂ в двоичной системе счисления означает одну четвёрку, одну единицу, одну половинку и одну четвертинку. Если сложить, получится всего 5.75₁₀.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления содержит 16 цифр - это цифры от 0 до 9 (соответствуют десятичным цифрам) и буквы от A до F, соответствие которых десятичным эквивалентам можно запомнить, а можно каждый раз в уме подсчитывать (10₁₀ - это А₁₆, 11₁₀ - это B₁₆, 12₁₀ - это C₁₆, 13₁₀ - это D₁₆, 14₁₀ - это E₁₆, а 15₁₀ - это F₁₆).

Все остальные правила, по которым представляются числа в разных позиционных системах счисления - абсолютно одинаковые. Меняется только количество используемых цифр, всё остальное - точно так же, как во всем привычной десятичной системе счисления.

Поэтому, Вы можете считать, что Вы разобрались с системами счисления, если Вы разобрались не только в каких-то определённых системах счисления (например, только в двоичной, восьмеричной, десятичной и шестнадцатеричной), а если Вы разобрались в любой системе счисления. В том числе, в троичной, в девятиричной, в двенадцатеричной, в двадцатисемиричной - и вообще в любой.

И поэтому, если в данный момент Вам ещё не понятно что-то с шестнадцатеричной системой счисления, то я рекомендовал бы Вам ещё раз прочитать и поглубже разобраться с тем, что написано выше на этой странице.

Непозиционные системы счисления

Непозиционные системы счисления - это такой способ записи чисел, в которых значение знака зависит не от позиции, а от каких-то других правил. Пример непозиционной системы счисления - всем известная римская система счисления. Для записи чисел в римской системе счисления используются римские цифры.

Хотя, строго говоря, римская система счисления не является полностью непозиционной. Так, меньшая цифра, записанная перед большей, вычитается из неё, а записанная после большей - прибавляется (то есть, значение цифры всё-таки зависит от позиции). Например, IV_{римская}=4₁₀, в то время как VI_{римская}=6₁₀.

Числа, не зависимо от системы счисления, всегда означают количество чего-нибудь. Собственно, записать число (в любой системе счисления) - это всего лишь способ записать это количество. Поэтому, можно составить таблицу соответствия между числами в разных системах счисления:

Для практического применения имеет смысл запомнить первые 16 строк этой таблицы (для чисел от 0 до 15). Но если разобраться в том, как эта таблица устроена, можно не запоминать, а научиться легко вычислять соответствие в уме.

Десятичная		Двоичная	Восьмеричная	Шестнадцатеричная	Римская
0		0	0	0	отсутствует
1		1	1	1	I
2		10	2	2	II
3		11	3	3	III
4		100	4	4	IV
5		101	5	5	V
6		110	6	6	VI
7		111	7	7	VII
8		1000	10	8	VIII
9		1001	11	9	IX
10		1010	12	A	X
11		1011	13	B	XI
12		1100	14	C	XII
13		1101	15	D	XIII
14		1110	16	E	XIV
15		1111	17	F	XV
16		10000	20	10	XVI
17		10001	21	11	XVII
18		10010	22	12	XVIII
19		10011	23	13	XIX
20		10100	24	14	XX
И так далее
	Перевод чисел из десятичной системы счисления в любую другую

При переводе чисел из десятичной системы счисления в любую другую, всегда отдельно (по разным правилам) переводится целая и дробная части.