3. Спектр колебания при смешанной амплитудно- частотной модуляции

О бобщим выражения (3.25), (3.26), заменив в них постоянную амплитуду A₀ функцией времени A (t):

Определение спектра сводится к нахождению спектров функций ₍ т. е. огибающих квадратурных колебании, и к последующему сдвигу этих спектров на величину ω₀.

Обозначим спектральные плотности функций символами Тогда

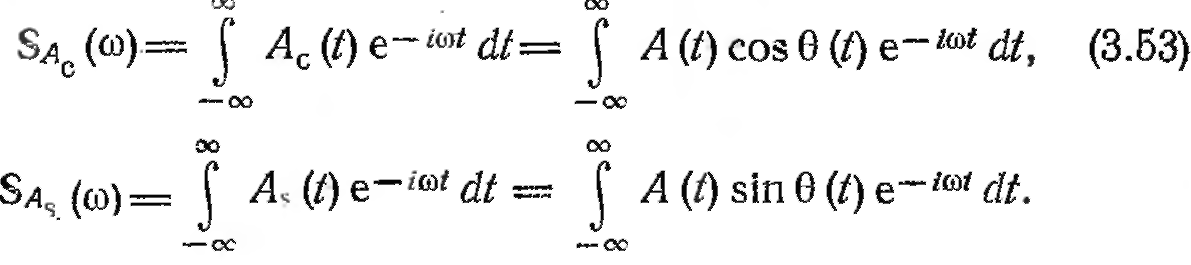
Спектральная плотность квадратурного колебания а_с (t)= =Ас(t)cos(ω₀t) в соответствии с выражением (2.58) (при θ_О = 0) будет

При определении спектра синусного квадратурного колебания фазовый угол θ в (2.58) следует приравнять—90°. Следовательно,

В области положительных частот можно считать

Таким образом, окончательно спектральная плотность колебания a (f) — а_с (t) — a_s (t) определяется выражением

Переходя к переменной получаем

Структура спектра колебания a (t) при смешанной амплитудно- частотной модуляции зависит от соотношения и вида функций А (t) и θ (t).

При чисто амплитудной модуляции спектр колебания a (t) характеризуется полной симметрией амплитуд и фаз колебаний боковых частот относительно несущего колебания; при чисто угловой модуляции симметричны только амплитуды,

фазы же колебаний боковых частот при нечетных п несимметричны относительно частоты ω Одновременная модуляция по амплитуде и углу может при некоторых соотношениях между A (t) и θ (t) приводить к асимметрии спектра относительно ω₀ не только по фазам, но и по амплитудам. В частности, если θ (t) является нечетной функцией t, то при любой функции A (t) спектр колебания a (t) несимметричен.

Действительно, пусть A (t) — четная функция. Тогда произведение — четная, а — нечетная функция t, и в соответствии со свойствами преобразования Фурье, перечисленными в § 2.7, п. 6, функция Sa_c (Ω) является вещественной и четной относительно Ω, а — мнимой и нечет- ной. С учетом множителя i второе слагаемое в (3.56) становится так- же вещественной, но нечетной функцией Ω и, следовательно, спектральная плотность S_Q (со) оказывается вещественной функцией, несимметричной относительно точки ω = ω₀. Пример подобного спектра представлен на рис. 3.21. (По отношению к точке ω = 0 модуль спектральной плотности симметричен при любых условиях.)

Аналогичный результат получается и при нечетной функции A (t). В этом случае — нечетная, мнимая функция Ω, а — четная

вещественная функция. Слагаемое в выражении (3.56) становится мнимым, и сумма становится функцией несимметричной (по модулю) относительно точки ω= ω₀.

С помощью аналогичных рассуждений нетрудно показать, что для симметрии спектра S_a (ω) требуется четность функции θ при одновременном условии, чтобы функция A (t) была либо чет- ной, либо нечетной функцией t. Если функция A (t) может быть представлена в виде суммы четной и нечетной составляющих, то спектр S_a (ω) несимметричен даже при четной функции θ (t). На- пример, импульс с линейной частотной модуляцией, рассмотренный в § 3.7, имеет симметричный спектр. В этом случае прямоугольная' огибающая при надлежащем выборе точки отсчета времени является функцией, четной относительно t, как и функция θ(t) = βt²

Наглядное представление о деформации спектра колебания при двойной модуляции — амплитудной и угловой — можно получить, рассмотрев случай, когда оба вида модуляции осуществляются одной и той же модулирующей функцией. Для упрощения анализа зададим эту функцию в виде гармонического колебания cos Ωt для угловой модуляции и в виде или для амплитудной.

1. Обе функции, как A (t), так и θ (t), четные относительно к

Выражение (3.52) принимает вид

Полагая, как в § 3.3, справедливыми приближенные равенства

приводим это выражение к виду, аналогичному (3.32):

Суммируя квадратурные составляющие получаем для амплитуды результирующего колебания на частоте ω₀ следующее выражение: при А_а = 1. Аналогичным образом находим амплитуду для колебаний с ча-

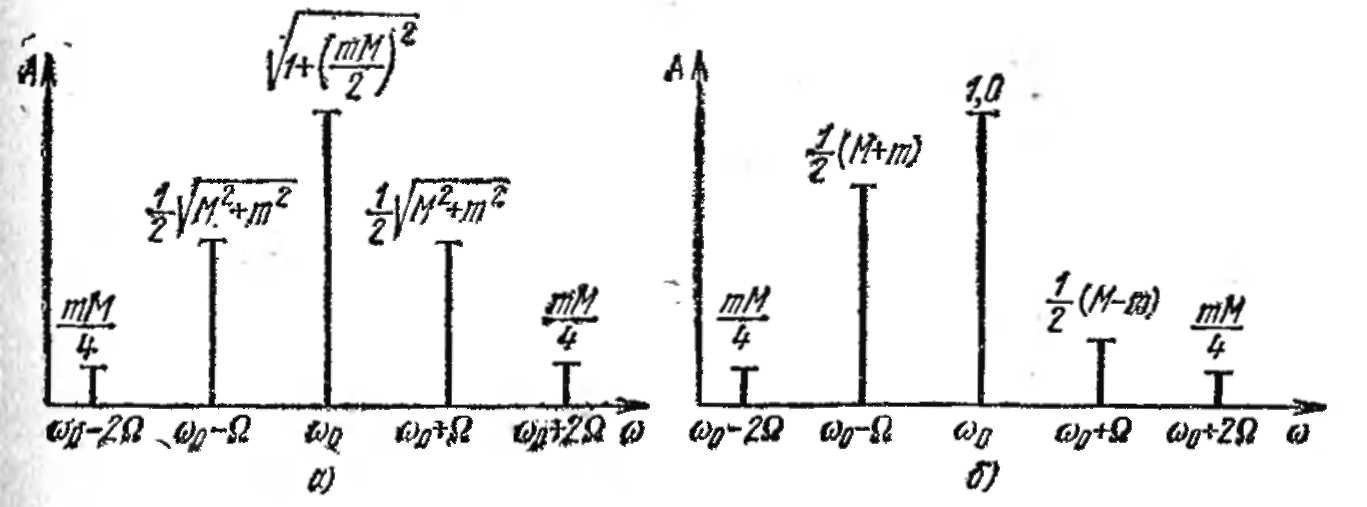
Рис. 3.22. Спектр колебания при одновременной модуляции амплитуды и частоты гармонической функцией.

стотами и для частот Спектр колебания

θ(t) представлен на рис. 3.22, а. Амплитудный спектр симметричен.

2. Функция θ(t) — четная, a A (t) — сумма четной и нечетной составляющих:

Выкладки, аналогичные предыдущим, приводят к следующим амплитудам: к 1 при частоте ω₀; к при частоте

^к при частоте при частотах

Спектральная диаграмма представлена на рис, 3.22, б.

Нарушение симметрии спектра при смешанной амплитудно частотной модуляции иногда используется как показатель неправильности работы устройства, осуществляющего амплитудную модуляцию; перекос спектра указывает на то, что полезная амплитудная модуляция сопровождается паразитной угловой модуляцией.