
Примеры решения задач
 Задача 1.
Определить длины диагоналей параллелограмма,
построенного на векторах
Задача 1.
Определить длины диагоналей параллелограмма,
построенного на векторах
![]() и
и
![]() ,
где
,
где
![]() таковы, что
таковы, что
![]() .
.
Решение.
Диагонали параллелограмма есть векторы
![]() и
и
![]() .
Вычислим длину вектора
:
.
Вычислим длину вектора
:
![]() .
.
Аналогично
вычисляется длина вектора
![]() .
.
Задача 2.
Найдите вектор
,
коллинеарный вектору
![]() и удовлетворяющий условию
и удовлетворяющий условию
![]() .
.
Решение.
Обозначим вектор
![]() ,
тогда из условий задачи
,
тогда из условий задачи
![]() или
или
![]() ,
,
тогда
![]() .
Итак:
.
Итак:
![]() .
.
Задача 3.
Найти проекцию вектора
![]() на направление вектора
на направление вектора
![]() .
.
Решение.
![]() .
По формуле проекции вектора на ось будет
иметь место равенство
.
По формуле проекции вектора на ось будет
иметь место равенство
![]() .
.
Задача 4.
Даны векторы:
![]() .
.
П
роверить,
есть ли среди них коллинеарные. Найти
![]() .
.
Решение.
Условие коллинеарности имеет вид
![]() .
Этому условию удовлетворяют векторы
.
Этому условию удовлетворяют векторы
![]() .
Следовательно, они коллинеарны. Найдем
длины
.
Следовательно, они коллинеарны. Найдем
длины
векторов
![]() :
:
![]() .
.
Угол между векторами
определяется по формуле
![]() .
.
Т
огда
![]() ,
,
![]() .
.
Используя формулу
![]() ,
получим
,
получим
![]() .
.
Задача 5.
На материальную точку действуют силы
![]() .
Найти работу равнодействующей этих сил
при перемещении точки из положения
.
Найти работу равнодействующей этих сил
при перемещении точки из положения
![]() в положение
в положение
![]() .
.
Решение.
Найдем силу
и вектор перемещения
![]() .
.
![]() ,
тогда искомая работа
,
тогда искомая работа
![]() .
.
Задачи
1. Векторы
взаимно перпендикулярны, а вектор
образует с ними углы
![]() .
Зная, что
.
Зная, что
![]() ,
найти: 1)
,
найти: 1)
![]() ;
2)
;
2)
![]() .
.
2. Вычислить длину
диагоналей параллелограмма, построенного
на векторах
![]() ,
если известно, что
,
если известно, что
![]() .
.
3. Доказать, что
вектор
![]() перпендикулярен к вектору
.
перпендикулярен к вектору
.
4. Зная, что
![]() ,
определить, при каком значении коэффициента
векторы
,
определить, при каком значении коэффициента
векторы
![]() окажутся перпендикулярными.
окажутся перпендикулярными.
5. Даны вершины
четырехугольника:
![]() .
Доказать, что его диагонали взаимно
перпендикулярны.
.
Доказать, что его диагонали взаимно
перпендикулярны.
6. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах
![]() .
.
7. Даны силы
![]() .
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку
.
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку
![]() .
.
8. Даны вершины
треугольника:
![]() .
Найти проекцию вектора
на вектор
.
.
Найти проекцию вектора
на вектор
.
9. Найти вектор
![]() ,
перпендикулярный векторам
,
перпендикулярный векторам
![]() ,
если известно, что его проекция на вектор
,
если известно, что его проекция на вектор
![]() равна единице.
равна единице.
10. Сила, определяемая
вектором
![]() ,
разложена по трем направлениям, одно
из которых задано вектором
,
разложена по трем направлениям, одно
из которых задано вектором
![]() .
Найти составляющую силы
в направлении вектора
.
.
Найти составляющую силы
в направлении вектора
.
11. Даны вершины
треугольника:
![]() .
Найти его внутренний угол при вершине
А и внешний угол при вершине В.
.
Найти его внутренний угол при вершине
А и внешний угол при вершине В.
12. Даны три
последовательные вершины параллелограмма:
![]() .
Найти его четвертую вершину D
и угол между векторами
.
Найти его четвертую вершину D
и угол между векторами
![]() .
.
13. На оси
![]() найти точку, равноудаленную от точек
найти точку, равноудаленную от точек
![]() .
.
14. Доказать, что
треугольник с вершинами
![]()
![]() прямоугольный.
прямоугольный.
Домашнее задание
1. Вычислить
скалярное произведение двух векторов
![]() ,
зная их разложение по трем единичным
взаимно перпендикулярным векторам
,
зная их разложение по трем единичным
взаимно перпендикулярным векторам
![]()
![]() ;
;
![]() .
.
2. Найти длину
вектора
![]() ,
зная, что
,
зная, что
![]() – взаимно перпендику-
– взаимно перпендику-
лярные орты.
3. Векторы
![]() попарно образуют друг с другом углы,
каждый из которых равен
.
Зная, что
попарно образуют друг с другом углы,
каждый из которых равен
.
Зная, что
![]() ,
определить модуль вектора
,
определить модуль вектора
![]() .
.
4. Доказать, что
вектор
![]() перпендикулярен к вектору
.
перпендикулярен к вектору
.
5. Даны векторы
![]() ,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису
,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису
![]() .
.
6. Вычислить угол
между векторами
![]() ,
где
,
где
![]() -
единичные взаимно перпендикулярные
векторы.
-
единичные взаимно перпендикулярные
векторы.
7. Даны силы
![]() ,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения
,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения
![]() в положение
в положение
![]() .
.
8. Даны вершины
треугольника
![]() .
Определить его внутренний угол при
вершине В.
.
Определить его внутренний угол при
вершине В.
9. Вычислив
внутренние углы треугольника с вершинами
![]() ,
,
![]() ,
убедиться, что этот треугольник
равнобедренный.
,
убедиться, что этот треугольник
равнобедренный.
10. Найти вектор
,
зная, что он перпендикулярен векторам
![]() и
и
![]() .
.
11. Найти вектор
,
коллинеарный вектору
![]() и удовлетворяющий условию
и удовлетворяющий условию
![]() ,
где
,
где
![]() .
.
12. Вычислить
проекцию вектора
![]() на ось вектора
на ось вектора
![]() .
.
13. Даны векторы
![]() .
Вычислить
.
Вычислить
![]() .
.
14. Даны точки
![]() .
Вычислить проекцию вектора
.
Вычислить проекцию вектора
![]() на ось вектора
на ось вектора
![]() .
.
Ответы к задачам
1) -7, 13. 2) 15,
![]() .
4)
.
4)
![]() .
6)
.
6)
![]() .
7) 2. 8) -1/3.
.
7) 2. 8) -1/3.
9)
![]() .
10)
.
10)
![]() .
11)
.
11)
![]() .
.
12)
![]() .
13)
.
13)
![]() .
.
Ответы к домашнему заданию
1) 9. 2) 5. 3) 10. 5)
![]() .
6)
.
6)
![]() .
7) 13. 8)
.
.
7) 13. 8)
.
10)
![]() .
12) 6. 13) 5. 14) 3.
.
12) 6. 13) 5. 14) 3.
Занятие 3
Векторое произведения векторов. Смешанное произведение векторов
Определение1. Тройка некомпланарных векторов называется правой (левой) если, находясь внутри телесного угла, образованного приведенными к общему началу векторами и от него к , човершающимся против часовой стрелки (по часовой стрелке)

![]()
Тройка правая Тройка левая
Определение
2. Векторным
произведением вектора
на вектор
называется вектор
![]() ,
длина и направление которого определяются
условиями:
,
длина и направление которого определяются
условиями:
1.
![]() ,
где
- угол между
,
где
- угол между
![]() .
.
2.
![]() .
.
3. - правая тройка векторов.
Свойства векторного произведения
1.
![]() (свойство антиперестановочности
сомножителей);
(свойство антиперестановочности
сомножителей);
2.
![]() (распределительное относительно суммы
векторов);
(распределительное относительно суммы
векторов);
3.
![]() (сочетательное относиельно числового
множителя);
(сочетательное относиельно числового
множителя);
4.
![]() (равенство нулю векторного произведения
означает коллинеарность векторов);
(равенство нулю векторного произведения
означает коллинеарность векторов);
5.
![]() ,
т. е. момент сил равен векторному
произведению силы на плечо.
,
т. е. момент сил равен векторному
произведению силы на плечо.
Если вектор
![]() ,
то
,
то
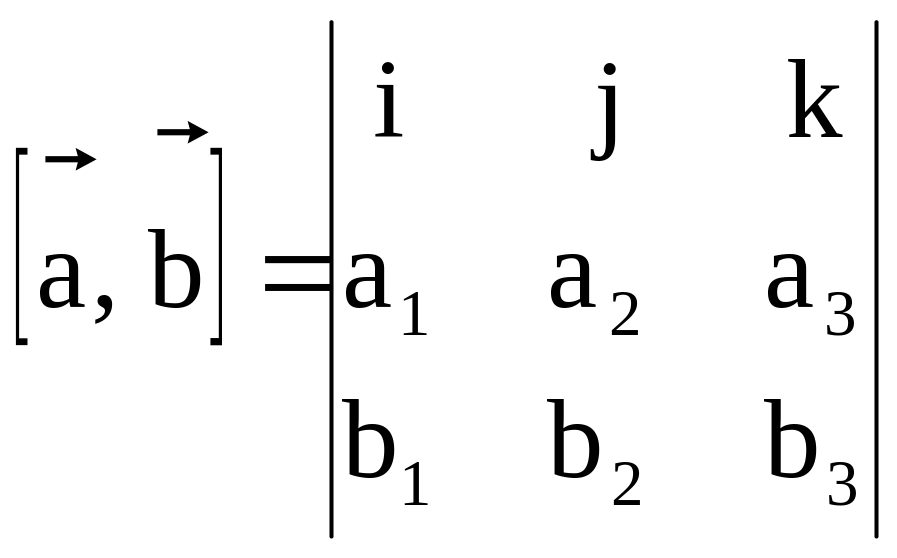 .
.
Определение
3. Смешанным
произведением
![]() трех векторов называется число,
определяемое следующим образом:
трех векторов называется число,
определяемое следующим образом:
![]() .
Если векторы заданы своими координатами:
.
Если векторы заданы своими координатами:
![]() ,
то
,
то
~
 .
.
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности векторов является равенство = 0.
2. Объем
параллелепипеда, построенного на
векторах
![]()
![]()
![]() :
:
![]()
