
- •Лекции по финансовой математике
- •Введение
- •1. Проценты
- •1.1. Виды процентных ставок
- •1.2. Наращение по простой процентной ставке
- •1.3. Дисконтирование по простым процентным ставкам и учет
- •1.4. Наращение по сложной процентной ставке
- •1.5. Наращение процентов m раз в году
- •1.6. Дисконтирование по сложной процентной ставке и учет
- •2. Типовые задачи
- •2.1. Погашение задолженности частями
- •2.2. Наращение и выплата процентов в потребительском кредите
- •2.3. Конверсия валюты и наращение процентов
- •2.4. Инфляция
- •2.5. Конверсия платежей
- •3. Потоки платежей
- •3.1. Виды потоков платежей и их основные параметры
- •3.2. Нерегулярные потоки платежей
- •3.3. Запаздывающие ренты
- •Формулы для расчета наращенной суммы s и современной стоимости a постоянных запаздывающих рент
- •Формулы для расчета срока постоянных запаздывающих рент
- •3.4. Другие виды рент
- •4. Страхование
- •4.1. Финансовые ренты в страховании
- •4.2. Вероятности дожития
- •4.3. Страхование жизни
- •4.4. Пенсионное страхование
- •4.5. Сберегательное (трастовое) обеспечение пенсий
- •5.Облигации
- •5.1. Основные понятия
- •5.2. Цена и доходность облигации
- •5.3. Временная структура процентных ставок
- •5.4. Риск портфеля облигаций
- •5.5. Форвардные контракты
- •6.Акции
- •6.1. Основные понятия
- •6.2. Портфель инвестиций
- •6.3. Модель оптимизации портфеля
- •6.4. Задача Марковица
- •6.5. Модель эволюции цен акций
- •7. Фьючерсы и опционы
- •7.1. Фьючерсы
- •7.2. Опционы
- •7.3. Биномиальная модель оценки стоимости опционов
- •Литература
- •Оглавление
2.2. Наращение и выплата процентов в потребительском кредите
В потребительском кредите проценты начисляются на всю сумму кредита и присоединяются к основному долгу уже в момент открытия кредита. Этот метод называется разовым начислением процентов. Погашение долга с процентами производится частями (обычно равными суммами) на протяжении всего срока кредита.
В этом случае наращенная сумма долга, при использовании сложной процентной ставки, равна
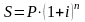 ,
,
а величина разового погасительного платежа R составит
R
=
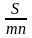 ,
(2.2)
,
(2.2)
где - срок кредита в годах;
- число платежей в году.
Заметим, что проценты начисляются на первоначальную сумму долга, в то время как его фактическая величина систематически уменьшается. В связи с этим действительная стоимость кредита заметно превышает договорную процентную ставку.
Пример 2.3. а) Кредит для покупки товара на сумму 1 млн руб. открыт на три года, процентная ставка - 30% годовых, платежи в конце каждого месяца. Сумма долга с процентами:
Ежемесячные платежи:
R =
б) Кредит на сумму 10000 руб. открыт на 10 месяцев, процентная ставка - 30% годовых, платежи в конце каждого месяца. Так как срок кредита менее 1 года, используются простые проценты. Сумма долга с процентами:
Ежемесячные платежи:
Заметим, что обычный кредит по той же процентной ставке погашается ежемесячными платежами по 1123,6 руб. в) Беспроцентный кредит на сумму 10000 руб. открыт на 10 месяцев, платежи в конце каждого месяца. При приеме платежей банк берет 1,5 % от оставшейся суммы за кассовое обслуживание. Платежи будут равны: 1150; 1135; 1120; 1105; 1090; 1075; 1060; 1045; 1030; 1015 руб. Такие платежи фактически соответствуют кредиту, выданному под 19,8 % годовых. 2,5 % от оставшейся суммы за кассовое обслуживание будет соответствовать кредиту, выданному под 35,2 % годовых. |
2.3. Конверсия валюты и наращение процентов
При возможности обмена рублевых средств на СКВ и наоборот целесообразно сравнить результаты от непосредственного размещения имеющихся денежных средств в депозиты или опосредованно через другую валюту.
Возможны четыре варианта:
без конверсии: СКВ - СКВ;
с конверсией: СКВ - Руб. - Руб. - СКВ;
без конверсии: Руб. - Руб.;
с конверсией: Руб. - СКВ - СКВ - Руб.
Варианты с конверсией показаны на рис. 2.3.
(СКВ) (СКВ) (Руб) (Руб)
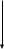

 (Руб)
(Руб)
(СКВ)
(СКВ)
(Руб)
(Руб)
(СКВ)
(СКВ)
а) б)
Рис.2.3
В операции наращения с конверсией валют два источника дохода: изменение курса и наращение, причем если второй из них безусловный (процентная ставка фиксирована), то первый заранее неизвестен. Более того, двойное конвертирование валюты может быть и убыточным.
В качестве примера рассмотрим вариант наращения по простым процентам с конверсией СКВ - Руб. - Руб. - СКВ.
Обозначим:
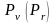 - сумма депозита в СКВ (в рублях);
- сумма депозита в СКВ (в рублях);
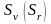 - наращенная сумма
в СКВ (в рублях);
- наращенная сумма
в СКВ (в рублях);
 - курс обмена в
начале операции (курс СКВ в руб.);
- курс обмена в
начале операции (курс СКВ в руб.);
- курс обмена в конце операции;
- срок депозита;
- ставка наращения для рублевых сумм;
- ставка наращения для конкретного вида СКВ.
Операция состоит из трех этапов: обмен валюты на рубли, наращение процентов на эту сумму и конвертирование в исходную валюту. Конечная (наращенная) сумма в валюте
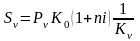 (2.3)
(2.3)
Множитель наращения с учетом двойного конвертирования
m
=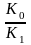 (1+ni)
=
(1+ni)
=
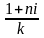 ,
(2.4)
,
(2.4)
где
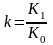 - темп роста курса валюты.
- темп роста курса валюты.
Пример 2.4. Предполагается поместить $1000 на рублевый депозит. Курс продажи на начало срока депозита 1500 руб. за $1, ожидаемый курс покупки - 1820 руб. (данные середины 1994 г.). Процентные ставки: = 220%, = 15%. Срок депозита - 3 месяца.
Прямое наращение по долларовой ставке дает = 1000 (1 + 0,15) = 1037,5 |
Поскольку в момент заключения контракта величина неизвестна, то определим максимально допустимое ее значение, при котором эффективность будет равна существующей ставке по депозитам в СКВ и применение двойного конвертирования не дает никакой дополнительной выгоды. Множители наращения в этом случае равны
(1 + nj) = (1+ni)
Отсюда следует
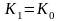
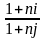 ;
(2.5)
;
(2.5)
Пример 2.5. Продолжим анализ операции из примера 2.4. Пусть необходимо принять решение до проведения операции. Величина курса на конец срока неизвестна. Максимально допустимое значение курса составит
= 1500
Если в начале операции ожидают, что курс доллара в рублях в конце срока будет меньше 2241 руб., то выгоднее применить конверсию, если же он будет больше, то целесообразнее непосредственный депозит в СКВ. |

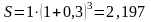 млн руб.
млн руб.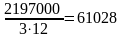 руб.
руб. руб.
руб.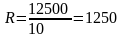 руб.
руб.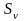 = 1000
= 1000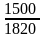 (1
+
(1
+
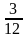 2,2)
= 1277,47
2,2)
= 1277,47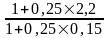 = 2241 руб.
= 2241 руб.