
- •Лекции по финансовой математике
- •Введение
- •1. Проценты
- •1.1. Виды процентных ставок
- •1.2. Наращение по простой процентной ставке
- •1.3. Дисконтирование по простым процентным ставкам и учет
- •1.4. Наращение по сложной процентной ставке
- •1.5. Наращение процентов m раз в году
- •1.6. Дисконтирование по сложной процентной ставке и учет
- •2. Типовые задачи
- •2.1. Погашение задолженности частями
- •2.2. Наращение и выплата процентов в потребительском кредите
- •2.3. Конверсия валюты и наращение процентов
- •2.4. Инфляция
- •2.5. Конверсия платежей
- •3. Потоки платежей
- •3.1. Виды потоков платежей и их основные параметры
- •3.2. Нерегулярные потоки платежей
- •3.3. Запаздывающие ренты
- •Формулы для расчета наращенной суммы s и современной стоимости a постоянных запаздывающих рент
- •Формулы для расчета срока постоянных запаздывающих рент
- •3.4. Другие виды рент
- •4. Страхование
- •4.1. Финансовые ренты в страховании
- •4.2. Вероятности дожития
- •4.3. Страхование жизни
- •4.4. Пенсионное страхование
- •4.5. Сберегательное (трастовое) обеспечение пенсий
- •5.Облигации
- •5.1. Основные понятия
- •5.2. Цена и доходность облигации
- •5.3. Временная структура процентных ставок
- •5.4. Риск портфеля облигаций
- •5.5. Форвардные контракты
- •6.Акции
- •6.1. Основные понятия
- •6.2. Портфель инвестиций
- •6.3. Модель оптимизации портфеля
- •6.4. Задача Марковица
- •6.5. Модель эволюции цен акций
- •7. Фьючерсы и опционы
- •7.1. Фьючерсы
- •7.2. Опционы
- •7.3. Биномиальная модель оценки стоимости опционов
- •Литература
- •Оглавление
1.4. Наращение по сложной процентной ставке
Формула наращения. В средне- и долгосрочных финансово-кредитных операциях обычно проценты присоединяются к сумме долга, а для наращения применяют сложные проценты. Присоединение начисленных процентов к сумме, которая служила базой для их начисления, называется капитализацией процентов.
Запишем формулу для расчета наращенной суммы при условии, что проценты начисляются и капитализируются один раз в году.
Очевидно,
что в конце первого года проценты равны
,
а наращенная сумма составит
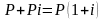 .
К концу второго года она достигает
величины
.
К концу второго года она достигает
величины
 и т.д.
и т.д.
В конце n-го года она будет
 (1.8)
(1.8)
Проценты за этот же период равны
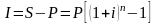 (1.9)
(1.9)
Проценты за каждый последовательный год увеличиваются. Для некоторого промежуточного года t они равны
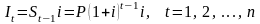 (1.10)
(1.10)
Г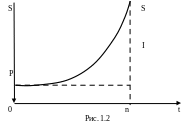 рафическая
иллюстрация роста по сложным процентам
на рис. 1.2. Величину
рафическая
иллюстрация роста по сложным процентам
на рис. 1.2. Величину
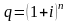 называют множителем наращения по
сложным процентам.
называют множителем наращения по
сложным процентам.
Пример 1.7. Какой величины достигнет долг, равный 1000 рублей, через 4 года при росте по сложной ставке 15% годовых?
|
Формула (1.8) получена для годовой процентной ставки и срока в годах. Однако ее можно применять и при других периодах начисления. В этих случаях - ставка за период начисления, - число таких периодов.
Переменные ставки. Если значения переменных ставок фиксируются в контракте, получаем
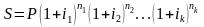 ,
,
где
 - последовательные во времени значения
ставок;
- последовательные во времени значения
ставок;
 - соответствующие
этим ставкам периоды.
- соответствующие
этим ставкам периоды.
Пример 1.8. Срок ссуды - 5 лет, договорная процентная ставка – 12% годовых в первые два года и 15% - в оставшиеся. Множитель наращения в этом случае
|
Рост
по сложным и простым процентам. Для
сопоставления результатов наращения
достаточно сравнить соответствующие
множители наращения. Для ставки простых
процентов введем индекс
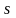 .
Получим следующие соотношения множителей
наращения:
.
Получим следующие соотношения множителей
наращения:
срок
меньше года
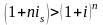 ;
;
срок
равен году
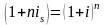 ;
;
срок
больше года
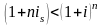 .
.
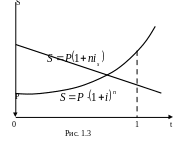
Графическая иллюстрация соотношения множителей наращения приведена на рис. 1.3.
1.5. Наращение процентов m раз в году
Номинальная ставка. Обычно проценты капитализируются несколько раз в году - по полугодиям, кварталам и т.д. Как правило, в контрактах фиксируется годовая ставка и одновременно указывается период начисления процентов, например “18% годовых с поквартальным начислением процентов”.
Пусть
-количество
лет, годовая ставка равна
 ,
число периодов начисления в году -
.
Каждый раз проценты начисляются по
ставке
,
число периодов начисления в году -
.
Каждый раз проценты начисляются по
ставке
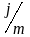 .
Ставку
называют номинальной.
.
Ставку
называют номинальной.
Формула наращения в этом случае
 (1.11)
(1.11)
Пример 1.9. Изменим
условия примера 1.7. Какой величины
достигнет долг, равный 1000 рублей, через
4 года при росте по сложной ставке 15%
годовых, если проценты начисляются
поквартально? В этом случае
При начислении процентов один раз в год получили = 1749 руб. |
Очевидно, чем чаще начисляются проценты, тем быстрее идет процесс наращения.
Эффективная ставка. Эффективная процентная ставка измеряет тот реальный относительный доход, который получают в целом за год от начисления процентов. это годовая ставка сложных процентов, которая дает тот же результат, что и -разовое начисление процентов по ставке .
Обозначим эффективную ставку . По определению множители наращения по двум видам ставок (эффективной и номинальной при m-разовом начислении) должны быть равны друг другу:
 =
(1 +
=
(1 +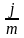 )mn
,
)mn
,
откуда = (1 + )m -1 (1.12)
Эффективная
ставка при
> 1 больше номинальной, при
= 1
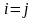 .
.
Пример 1.10. Какова эффективная ставка, если номинальная ставка 25% при помесячном начислении процентов?
= (1 +
Для сторон в сделке безразлично: применить ставку 25% (при помесячном начислении) или годовую ставку 28,07% |
При подготовке контрактов может возникнуть необходимость в решении обратной задачи - в определении j по заданным значениям и . Находим
 .
(1.13)
.
(1.13)

 руб.
руб. = (1 + 0,12)2(1 +
0,15)3 = 1,9078
= (1 + 0,12)2(1 +
0,15)3 = 1,9078 =16
и
=16
и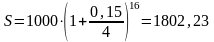 руб.
руб. )12
- 1 = 0,2807
)12
- 1 = 0,2807