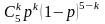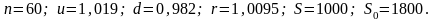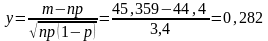- •Лекции по финансовой математике
- •Введение
- •1. Проценты
- •1.1. Виды процентных ставок
- •1.2. Наращение по простой процентной ставке
- •1.3. Дисконтирование по простым процентным ставкам и учет
- •1.4. Наращение по сложной процентной ставке
- •1.5. Наращение процентов m раз в году
- •1.6. Дисконтирование по сложной процентной ставке и учет
- •2. Типовые задачи
- •2.1. Погашение задолженности частями
- •2.2. Наращение и выплата процентов в потребительском кредите
- •2.3. Конверсия валюты и наращение процентов
- •2.4. Инфляция
- •2.5. Конверсия платежей
- •3. Потоки платежей
- •3.1. Виды потоков платежей и их основные параметры
- •3.2. Нерегулярные потоки платежей
- •3.3. Запаздывающие ренты
- •Формулы для расчета наращенной суммы s и современной стоимости a постоянных запаздывающих рент
- •Формулы для расчета срока постоянных запаздывающих рент
- •3.4. Другие виды рент
- •4. Страхование
- •4.1. Финансовые ренты в страховании
- •4.2. Вероятности дожития
- •4.3. Страхование жизни
- •4.4. Пенсионное страхование
- •4.5. Сберегательное (трастовое) обеспечение пенсий
- •5.Облигации
- •5.1. Основные понятия
- •5.2. Цена и доходность облигации
- •5.3. Временная структура процентных ставок
- •5.4. Риск портфеля облигаций
- •5.5. Форвардные контракты
- •6.Акции
- •6.1. Основные понятия
- •6.2. Портфель инвестиций
- •6.3. Модель оптимизации портфеля
- •6.4. Задача Марковица
- •6.5. Модель эволюции цен акций
- •7. Фьючерсы и опционы
- •7.1. Фьючерсы
- •7.2. Опционы
- •7.3. Биномиальная модель оценки стоимости опционов
- •Литература
- •Оглавление
6.4. Задача Марковица
Рассмотрим
модель инвестирования в
акций. Из всех допустимых портфелей
,
ожидаемая доходность которых
равна заданному уровню
,
инвестора интересует портфель с
минимальным риском, определямым его
дисперсией
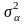 .
Формально задача имеет вид:
.
Формально задача имеет вид:
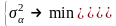
Воспользовавшись формулами (6.4), (6.5) запишем задачу Марковица:
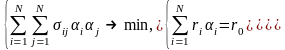 (6.16)
(6.16)
Это задача оптимизации с нелинейной целевой функцией и ограничениями. Для ее решения можно использовать различные методы. Будем искать решение используя метод неопределенных множителей Лагранжа. Целевая функция
 .
.
В точке экстремума производные равны нулю:
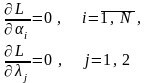 (6.17)
(6.17)
Найдем эти частные производные:
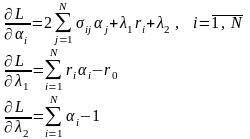
Приравниваем производные нулю:

В
матричной форме записи

А-
симметричная матрица
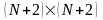 :
:
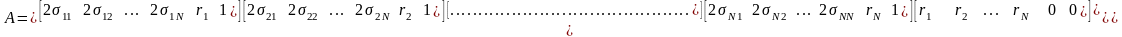 ;
;
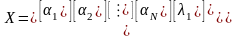 ;
;
 .
.
Решая систему уравнений в матричном виде получаем решение:

Так
как в векторе
 ненулевыми являются только два последних
элемента, а в векторе
нас интересуют первые
координат, портфель инвестиций
определяется блоком обратной матрицы
из
строк и последних двух столбцов.
Действительно, для любого
ненулевыми являются только два последних
элемента, а в векторе
нас интересуют первые
координат, портфель инвестиций
определяется блоком обратной матрицы
из
строк и последних двух столбцов.
Действительно, для любого
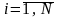
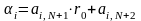 (6.18)
(6.18)
Изменяя значения желаемой доходности, мы всегда получаем оптимальный портфель, а вместе с ним и минимальное СКО, ему соответствующее. Таким образом, это позволяет нам построить границу области допустимых точек на плоскости “риск-доходность”.
Пример 6.2. Инвестиции возможны в акции трех типов. Известна ожидаемая доходность и матрица ковариации, надо найти вектор :
Тогда
матрица
и ее обратная
По
формуле (6.18) находим
Пусть
доходность портфеля 20%, то есть
Найдем риск портфеля инвестиций по формуле (6.16). В матричной форме
|
Заметим, что если в
портфель инвестиций включается
безрисковый актив с доходностью
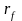 ,
задача решается аналогично. Нас будут
интересовать портфели
,
задача решается аналогично. Нас будут
интересовать портфели
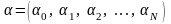 ,
где
,
где
 - доля капитала, инвестированного в
безрисковый актив с нулевым риском
- доля капитала, инвестированного в
безрисковый актив с нулевым риском
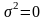 и нулевой ковариацией
и нулевой ковариацией
 .
.
6.5. Модель эволюции цен акций
Если
взглянуть на графики цен акций, то видно,
что их поведение носит стохастический
характер. Значение цены акции
 в момент времени
является случайной величиной. Если к
тому же рассмотреть эволюцию цены акции
во времени
в момент времени
является случайной величиной. Если к
тому же рассмотреть эволюцию цены акции
во времени
 ,
то она определяет некий случайный
процесс.
,
то она определяет некий случайный
процесс.
С начала
рассмотрим простейшую модель эволюции
цены, когда рассматриваются цены только
в начале и конце периода. Предполагается,
что цена акции может либо вырасти с
коэффициентом
начала
рассмотрим простейшую модель эволюции
цены, когда рассматриваются цены только
в начале и конце периода. Предполагается,
что цена акции может либо вырасти с
коэффициентом
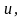 либо упасть с коэффициентом
либо упасть с коэффициентом
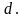 Если обозначить начальную цену акции
Если обозначить начальную цену акции
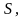 то в конце единичного периода она может
быть либо
то в конце единичного периода она может
быть либо
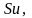 либо
либо
 (Рис. 6.6). Пусть
(Рис. 6.6). Пусть
 - коэффициент роста при инвестировании
в безрисковый актив.
- коэффициент роста при инвестировании
в безрисковый актив.
 (6.19)
(6.19)
Обозначим
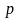 -
вероятность того, что цена возрастет.
Тогда
-
вероятность того, что цена возрастет.
Тогда
 - вероятность падения цены.
- вероятность падения цены.


Если инвестор нейтрален к риску, для него эквивалентно инвестирование денег в покупку акции или в безрисковый актив одной и той же доходности. Это значит, что выполнено равенство:
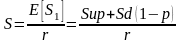 .
.
После сокращения получим:
 .
(6.20)
.
(6.20)
Отсюда
найдем
 .
.
Дерево возможных эволюций цены для трех периодов приведено на рис. 6.7.
Результат каждого периода мы можем охарактеризовать случайной величиной

Рассмотрим случайную величину - количество периодов из общего их числа , когда цена растет. Такая случайная величина имеет биномиальное распределение:
 .
.
Следовательно
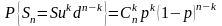 (6.21)
(6.21)
Предположим, что задается некоторый критичный уровень цены акции после периодов , ниже которого она не должна опуститься.
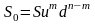 ,
,
где - наименьшее значение количества периодов возрастания цены акции.
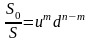 ,
,
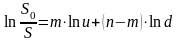
отсюда
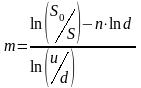 (6.22)
(6.22)
В
расчетах используется
 - ближайшее целое, не превосходящее
- ближайшее целое, не превосходящее
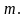
Тогда вероятность того, что в момент времени цена акции превосходит заданный уровень :
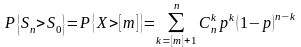 (6.23)
(6.23)
Из
теории вероятностей известно, что
математическое ожидание случайной
величины, имеющей биномиальное
распределение равно

Следовательно, математическое ожидание цены акции через периодов
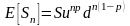 (6.24)
(6.24)
Пример 6.3. Необходимо получить прогноз будущей цены акции через 5 лет. Известно, что цена акции в течение каждого года может либо подняться на 25%, либо упасть на 20%, в то время как безрисковый актив дает 12% годовых. Требуется определить вероятностьтого, что цена акции в конце пятого года будет больше 1800 рублей, если текущая цена 1000 рублей. Параметры биномиальной модели будут следующими:
Сначала определим вероятности, нейтральные к риску.
Подставив заданные параметры в (7.23) получим
Соответственно
Тогда искомая вероятность находится по формуле (6.23)
Для
данного примера распределение случайной
величины
|
Биномиальная модель удобна при небольшом количестве периодов, но при росте их числа становится громоздкой. В этом случае используют аппроксимацию биномиального распределения нормальным законом.
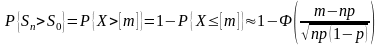 ,
(6.25)
,
(6.25)
где
 - функция Лапласа. Для этой функции
имеются таблицы.
- функция Лапласа. Для этой функции
имеются таблицы.
Пример 6.4. Необходимо (как в примере 6.3) получить прогноз цены акции через 5 лет. Какова вероятность того, что цена акции в конце пятого года будет больше 1800 рублей при условии, что начальная цена 1000 рублей. Ежемесячно цена либо увеличивается на 1,9%, либо уменьшается на 1,8%. При этом безрисковая ставка в месяц составляет 0,95%. Эти данные соответствуют примеру 6.3, но количество периодов резко выросло. Параметры
задачи:
Нейтральные к риску вероятности
По формуле (7.23) найдем критическое значение
Аргумент функции Лапласа равен
Используем таблицу Лапласа
|

 имеют
размер 5х5:
имеют
размер 5х5: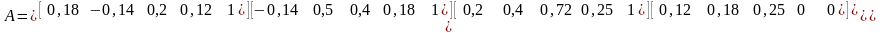
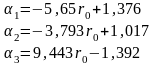
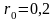 .
Тогда
.
Тогда


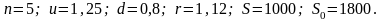

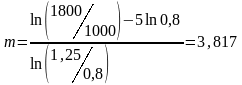
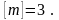

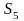 легко получить по формуле (6.21)
легко получить по формуле (6.21)