6.3. Модель оптимизации портфеля

Допустим, что у нас имеется две возможности инвестирования. Первая – в безрисковый актив с доходностью 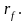Вторая – покупка акции (или портфеля акций), доходность по которой является случайной величиной 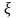с математическим ожиданием 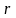и средним квадратическим отклонением

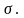
Портфель однозначно будет определяться долей капитала, инвестируемой в рисковый актив. Оставшаяся часть капитала будет вложена в безрисковый актив. Для каждого такого портфеля доходность определяется по формуле:

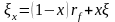(6.6)

Тогда ожидаемая доходность и среднее квадратическое отклонение доходности портфеля равны

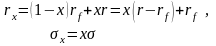(6.7)

Перед каждым инвестором стоит задача выбора оптимального портфеля по каким-то собственным критериям. Оптимальный портфель определяется конкретным значением 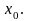Рассмотрим несколько вариантов этой задачи.

1. Максимум ожидаемой доходности. Предположим, что инвестор не интересуется риском и оптимизирует портфель, стараясь получать максимум ожидаемой доходности. Тогда задача формулируется так:

(6.8)

Решение зависит от знака коэффициента . В зависимости от него имеется три случая изменения 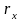, как функции параметра (рис. 6.2).

В случае а), когда функция возрастает и достигает максимума при 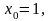то есть когда весь капитал вкладывается в рисковый актив.

В случае б) 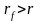, максимум достигается при когда портфель состоит только из безрискового актива.

Случай в), когда , и любой портфель может быть оптимальным.

Следует заметить, что второй третий случаи являются очевидными с точки зрения инвестора – он предпочтет безрисковый актив Далее будем рассматривать только неочевидный случай, когда

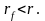
2. Задача Марковица. Допустим, что задан некоторый уровень доходности 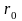, ниже которого инвестор не хотел бы иметь ожидаемую доходность. Тогда оптимальный портфель выбирается среди всех возможных так, чтобы риск инвестиций был минимальным:

(6.9)

О чевидно, что (рис. 6.3).

Составляем пропорцию 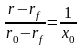и находим долю инвестиций в рисковый актив - .

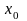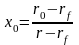(6.10)

Соответственно

(6.11)

Таким образом, оптимальный портфель в задаче Марковица в простейшем случае безрискового и рискового активов определяется следующей парой:

3. Соотношение “риск-доходность”. Предположим, что предпочтение инвестора определяется минимизацией некоторой функции, связывающей риск и доходность портфеля. Введем функцию рискованности, например, следующим образом:

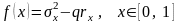
Коэффициент определяет предпочтения инвестора. Если для инвестора важнее доходность, а не риск, то он выбирает коэффициент с большим значением. Если более важным является риск, то он выберет маленьким.

После подстановки из (6.7), задача оптимизации портфеля имеет следующий формальный вид:

(6.12)

Функция является параболой, ветви которой направлены вверх 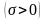. Значит функция имеет минимум в вершине

(6.13)

Рассмотрим два варианта выбора оптимального портфеля.

1) 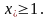Так как в этом случае функция убывает на отрезке 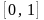, ее минимум достигается в точке

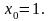
Очевидно, что неравенство 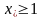эквивалентно условию

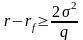или (6.14)

2) Если это неравенство не выполнено и имеет место соотношение

,

то 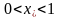и минимум функции на отрезке достигается в точке 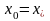. Тогда оптимальный портфель имеет распределение капитала 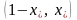. Из (6.13) получаем его окончательный вид:

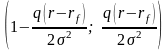. (6.15)

В этом случае ожидаемая доходность и среднее квадратическое отклонение оптимального портфеля равны

.

Заметим, что в (6.14) рисковая надбавка. Ее величина зависит от предпочтений инвестора (он определяет величину ). Если доходность рискового актива больше, чем доходность безрискового актива плюс рисковая надбавка, инвестор предпочтет рискнуть и вложить весь капитал в рисковый актив. Однако, если эта надбавка столь велика, что неравенство (6.14) не выполняется, то инвестор распределяет капитал в соответствии с (6.15).

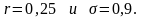
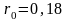Пример 6.1. Необходимо оптимизировать портфель, состоящий из рискового и безрискового активов. Доходность безрискового актива 12%, то есть , а доходность и СКО рискового актива равны Максимум ожидаемой доходности. Оптимальный портфель состоит из инвестиций только в рисковый актив: (0, 1). Задача Марковица. Допустим инвестор согласен на ожидаемую доходность , но при этом хотел бы минимизировать риск.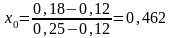 , следовательно, оптимальный портфель (0,538; 0,462). Соотношение “риск-доходность”. Пусть . Тогда . 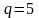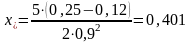Оптимальный портфель (0,599; 0,401).