
- •Лекции по финансовой математике
- •Введение
- •1. Проценты
- •1.1. Виды процентных ставок
- •1.2. Наращение по простой процентной ставке
- •1.3. Дисконтирование по простым процентным ставкам и учет
- •1.4. Наращение по сложной процентной ставке
- •1.5. Наращение процентов m раз в году
- •1.6. Дисконтирование по сложной процентной ставке и учет
- •2. Типовые задачи
- •2.1. Погашение задолженности частями
- •2.2. Наращение и выплата процентов в потребительском кредите
- •2.3. Конверсия валюты и наращение процентов
- •2.4. Инфляция
- •2.5. Конверсия платежей
- •3. Потоки платежей
- •3.1. Виды потоков платежей и их основные параметры
- •3.2. Нерегулярные потоки платежей
- •3.3. Запаздывающие ренты
- •Формулы для расчета наращенной суммы s и современной стоимости a постоянных запаздывающих рент
- •Формулы для расчета срока постоянных запаздывающих рент
- •3.4. Другие виды рент
- •4. Страхование
- •4.1. Финансовые ренты в страховании
- •4.2. Вероятности дожития
- •4.3. Страхование жизни
- •4.4. Пенсионное страхование
- •4.5. Сберегательное (трастовое) обеспечение пенсий
- •5.Облигации
- •5.1. Основные понятия
- •5.2. Цена и доходность облигации
- •5.3. Временная структура процентных ставок
- •5.4. Риск портфеля облигаций
- •5.5. Форвардные контракты
- •6.Акции
- •6.1. Основные понятия
- •6.2. Портфель инвестиций
- •6.3. Модель оптимизации портфеля
- •6.4. Задача Марковица
- •6.5. Модель эволюции цен акций
- •7. Фьючерсы и опционы
- •7.1. Фьючерсы
- •7.2. Опционы
- •7.3. Биномиальная модель оценки стоимости опционов
- •Литература
- •Оглавление
6.2. Портфель инвестиций
Рассмотрим
модель инвестирования капитала на
единицу времени в экономику, состоящую
из
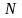 типов акций. Будем полагать, что через
единицу времени все фирмы ликвидируются,
а полученные доходы распределяются
среди акционеров. Дивиденды, выплачиваемые
на акции каждого типа, будем считать
случайными величинами.
типов акций. Будем полагать, что через
единицу времени все фирмы ликвидируются,
а полученные доходы распределяются
среди акционеров. Дивиденды, выплачиваемые
на акции каждого типа, будем считать
случайными величинами.
Обозначим
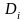 - дивиденд, выплачиваемый на акцию
- дивиденд, выплачиваемый на акцию
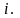 Пусть
Пусть
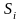 - цена акции
в начальный момент времени. Тогда
доходность акции
- цена акции
в начальный момент времени. Тогда
доходность акции
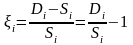 (6.1)
(6.1)
Так
как это случайная величина, то используют
ее математическое ожидание
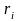 и дисперсию
и дисперсию
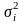 .
Квадратный корень из дисперсии называют
средним квадратическим отклонением
.
Квадратный корень из дисперсии называют
средним квадратическим отклонением
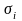 .
.
Таким
образом, каждой акции
ставят в соответствие ожидаемую
доходность
и среднее квадратическое отклонение
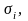
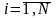 .
Взаимная зависимость акций определяется
матрицей ковариации
.
Взаимная зависимость акций определяется
матрицей ковариации
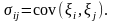 В частности
В частности
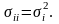
Рассмотрим
теперь некоторого инвестора, имеющего
капитал
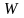 и желающего весь его инвестировать в
акции с целью получения дохода через
единицу времени. Допустим, что
и желающего весь его инвестировать в
акции с целью получения дохода через
единицу времени. Допустим, что
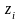 - число акций типа
,
купленных в начальный период. Тогда
- число акций типа
,
купленных в начальный период. Тогда
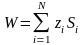 (6.2)
(6.2)
Обозначим
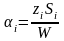 (6.3)
(6.3)
долю инвестиций в акции типа Набор действительных чисел
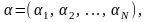
удовлетворяющих
условию
 называется портфелем инвестиций.
называется портфелем инвестиций.
Доходность портфеля инвестиций будет складываться из доходностей отдельных акций. Доходность портфеля инвестиций и его дисперсия определяются по формулам:
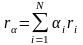 (6.4)
(6.4)
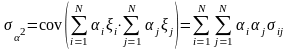 (6.5)
(6.5)
Для каждого допустимого портфеля на плоскости “риск-доходность” можно отметить точки, координаты которых равны среднему квадратическому отклонению и ожидаемой доходности портфеля.
Рисунок
6.1 показывает возможные соотношения
между риском и доходностью на данном
рынке. Каждая точка области соответствует
портфелю инвестиций. Если инвестор
заинтересован в максимизации ожидаемой
доходности
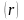 и минимизации риска
и минимизации риска
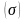 ,
то для него играет роль правило левого
верхнего угла. Суть его: если выбрать
некоторый портфель
,
то для него играет роль правило левого
верхнего угла. Суть его: если выбрать
некоторый портфель
 и на соответствующей ему точке построить
левый верхний угол, то любой портфель
и на соответствующей ему точке построить
левый верхний угол, то любой портфель
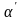 с соответствующей ему точкой из
построенного угла является для инвестора
более предпочтительным.
с соответствующей ему точкой из
построенного угла является для инвестора
более предпочтительным.
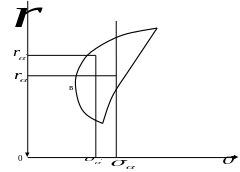
Рис. 6.1
Для
каждого допустимого значения доходности
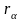 можно выбрать граничную точку,
соответствующую портфелю инвестиций
с заданной ожидаемой доходностью и
наименьшим риском. На рис. 6.1 для заданной
доходности
это точка В.
можно выбрать граничную точку,
соответствующую портфелю инвестиций
с заданной ожидаемой доходностью и
наименьшим риском. На рис. 6.1 для заданной
доходности
это точка В.
Понятно, что для инвестора координаты граничных точек и соответствующие им портфели являются наиболее важными с точки зрения оптимального выбора инвестиций, так как с учетом правила левого верхнего угла для любой внутренней точки области всегда найдется более предпочтительная точка на границе. Граница области выпукла влево, ее форма показана на рис. 6.1.
