6.3. Планетарные передачи.

Различают 4 основных типа планетарных ступеней (так называемых механизмов Давида) (рис.6.3, схемы І - ІV):

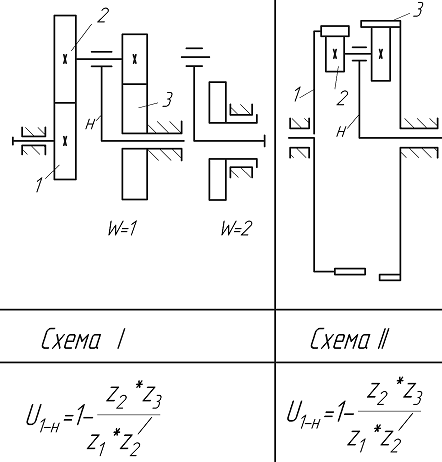
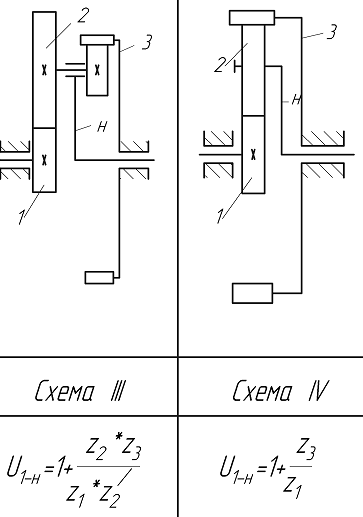
Рис.6.3. Кинематические схемы планетарных передач

Условные обозначения звеньев планетарных механизмов на рис. 6.3: 1 – центральное колесо, 2 – сателлиты, 3 – опорное (неподвижное) колесо; H – водило (от заглавной буквы слова Hedel – рычаг).

Преимущества планетарных передач:

- компактность при больших передаточных отношениях U;

- возможность передачи больших крутящих моментов (т.к. при их передаче используется несколько сателлитов);

Недостатки планетарных передач:

- сложность изготовления;

- требуются высокая точность изготовления и сборки.

6.3.1. Вычисление передаточного отношения планетарной передачи

Аналитический метод. Используем метод обращения движения – т.е. всему механизму, в том числе неподвижному колесу, условно придается (сообщается) угловая скорость - (то есть все звенья в таком механизме уменьшают скорость на величину угловой скорости водила ). Тогда в этом так называемом обращенном механизме водило H станет неподвижным, и мы получим простой ступенчатый механизм с неподвижными осями. Угловые скорости исходного планетарного и обращенного механизма сведем в таблицу:

№№ звеньев	Угловые скорости
	В планетарном механизме	В обращенном механизме
1 2 3 H

Вычисляем передаточные отношения обращенного механизма (на примере схемы I):

через угловые скорости (6.2)

через числа зубьев колес (6.3)

Из уравнений (6.2) и (6.3) получим:

Для других схем планетарных механизмов (рис. 6.3) выводы формул расчета передаточных отношений аналогично предыдущему.

Общая формула имеет вид

,

где - передаточное отношение обращенного механизма.

Графический метод расчета передаточного отношения планетарной передачи заключается в том, что сначала строят кинематическую схему механизма в масштабе, затем картину (план) линейных скоростей и картину угловых скоростей. Используя геометрические размеры построений, вычисляют передаточное отношение. Рассмотрим последовательность решения на примере механизма, изображенного на рис. 6.4.

Рис. 6.4. План механизма (а), картина линейных скоростей (б) и план угловых скоростей (в)

Последовательность решения

Строится кинематическая схема планетарного механизма в двух проекциях в выбранном масштабе (рис.6.4а). Для этого рекомендуется радиусы зубчатых колес (в мм) на схеме принимать равными числам зубьев (т.е. условно принимать модуль m = 2).

Строится план окружных линейных скоростей механизма в следующей последовательности. Из полюса зацепления 1 и 2 колес (точки Р₁₂ на правой проекции механизма) проводят вектор V_P12 произвольной длины. Он изображает линейную скорость точки P₁₂. Соединив конец этого вектора с точкой O₁, получают треугольник скоростей колеса 1. Здесь гипотенуза изображает изменение линейных скоростей колеса 1 от оси вращения до делительной окружности.

Строится треугольник скоростей звена 2. Для этого конец вектора V_P12 соединяют с неподвижным полюсом P₂₃ зацепления колес 2 и 3.

Строится треугольник скоростей водила Н. Для этого из точки O₂ проводят вектор линейной скорости V₀₂ до гипотенузы (прямой между точками P₂₃ и V_P12 ) треугольника скоростей сателлита 2. Соединив конец вектора V_O2 с точкой О_H гипотенузой, получают треугольник скоростей водила Н.

Как известно, величина передаточного отношения механизма равна отношению угловых скоростей (U_1-H = ₁/_Н). Величины угловых скоростей 1-го колеса ₁ и водила _Н пропорциональны тангенсам углов ₁и _Н на плане окружных линейных скоростей. Но так как углами при расчетах пользоваться не совсем удобно, то строится план частот вращения. Для этого проводят вертикальный отрезок ОР произвольной длины. Через точку О проводят горизонтальную линию. Из точки Р проводят под углами ₁, ₂, _Н к отрезку ОР линии Р1, Р2 и РН, параллельные гипотенузам треугольников окружных скоростей. Отрезки Р1, Р2 и РН пропорциональны частотам вращения звеньев I, 2 и Н. Для вычисления передаточных отношений достаточно измерить длины этих отрезков и подставить в нижеприведенные формулы. Причем, если соотносимые отрезки лежат по одну сторону от точки О, то передаточное отношение берется со знаком плюс, если по разные – со знаком минус:

U^гр_1-Н = О1/ОН, U^гр₁₂ = - О1/О2 .

При этих построениях принимается, что окружная линейная скорость точки А, принадлежащей колесу 1, равна

,

скорость точки О₂, принадлежащей сателлиту, равна

,

угловая скорость центрального колеса 1, равна

,

угловая скорость водила Н

,

а величина передаточного отношения от колеса 1 к водилу Н будет равна