3.3. Силовой анализ характерных структурных групп

3.3.1. Структурная группа 2-го класса 1-го вида

Известны: внешние силы и , а также точки их приложения К₂ и К₃.

Найти: реакции в кинематических парах А, В и С (рис.3.4.).

Последовательность решения:

1. Строим структурную группу в масштабе длин _L (рис.3.4).

2. Наносим на неё все внешние силы и .

3. В кинематических парах А и С действие отброшенных звеньев (например, кривошипа 1 и стойки 0) заменяем силами реакций и 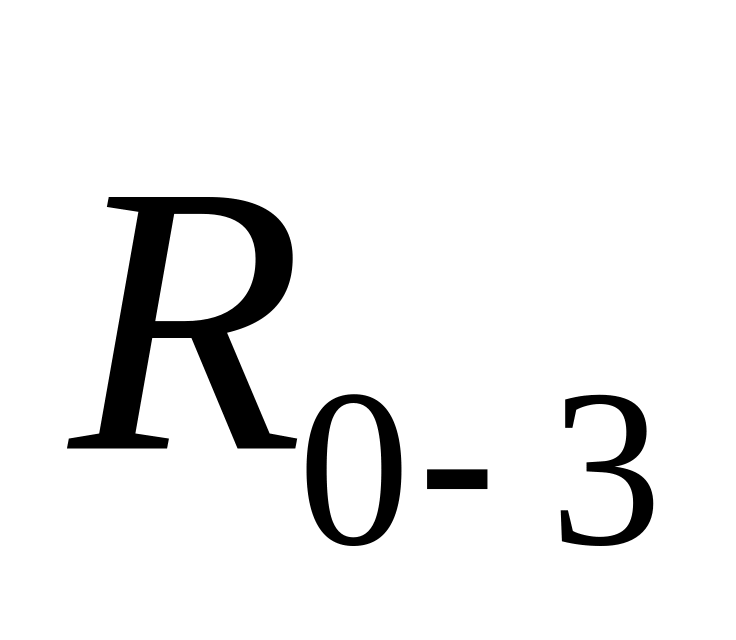, разложив каждую из них на нормальную и тангенциальную составляющие: = + и = + .

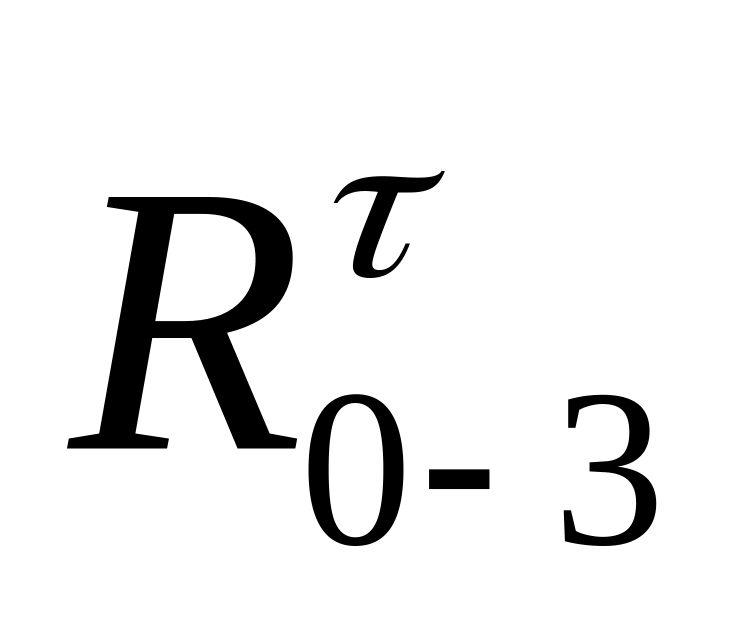4. Составляем уравнение равновесия структурной группы:

; или (3.1)

5. Вычисляем величины тангециальных сил; для этого используем условие, что моменты сил относительно точки В, приложенных к звеньям 2 и 3, равны нулю:

; , откуда ;

; , откуда .

Следует учитывать, что если в процессе решения эти тангенциальные силы получись с отрицательным знаком, то на плане структурной группы их предварительно выбранное направление следует поменять на противоположное.

6. Неизвестные 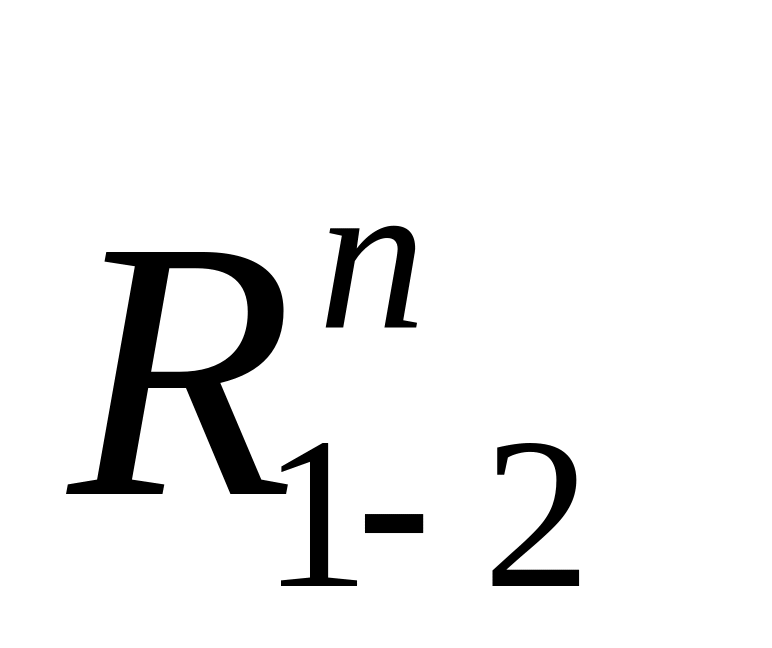и находим путём графического изображения векторного уравнения (3.1) в масштабе, то есть, строим план сил структурной группы.

Для построения плана сил выбираем масштаб плана сил: , Н/м, где – длина вектора в мм, изображающего силу на плане сил, выбирается произвольно. При выборе учитываются два условия: чтобы план сил разместился на отведённом месте чертежа, а масштаб был удобен для расчётов (был «круглым» числом).

Переводим (пересчитываем) силы уравнения (3.1) в векторные отрезки с длинами: , мм; , мм; , мм.

Тогда уравнение (3.1) запишется в виде

(3.2).

Построение плана сил ведём в последовательности написания уравнения (3.2) (рис. 3.5).

7. Вычисляем реакции:

,

где длины отрезков и берем в мм из плана сил.

8. Определяем реакцию в кинематической паре В. Для этого составляем векторное уравнение равновесия звена 2 или звена 3; например, условие равновесия звена 2 можно записать в виде:

, (3.3).

где R_3-2 – сила реакции в кинематической паре В.

Так как и известны, то, построив план сил звена 2 (рис. 3.6), то есть графически изобразив уравнение (3.3), получим силу :

.

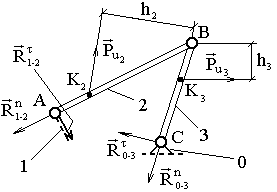
Рис. 3.4. План структурной группы 2 класса 1 вида

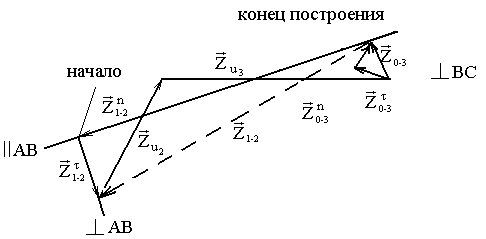
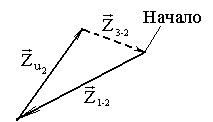
Рис. 3.5. План сил структурной группы Рис. 3.6. План сил звена 2

3.3.2. Структурная группа 2-го класса 2-го вида

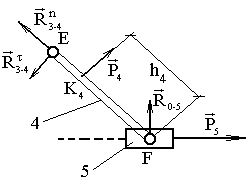
Рис. 3.7. План структурной группы 2 класса 2 вида

Условие равновесия структурной группы (рис. 3.7):

. (3.4)

Величина тангенциальной составляющей силы реакции в шарнире вычисляется по формуле, полученной из условия равенства нулю моментов всех сил, приложенных к шатуну 4, относительно точки F:

; ,

откуда находим ,

где h₄ – плечо силы Р₄ относительно точки F, берется из плана структурной группы (рис.3.5.), построенной в масштабе длин _L.

Силы и берут из плана сил, построенного с использованием уравнения (3.4) в выбранном масштабе , а силу находят из уравнения равновесия ползуна , построив план сил ползуна.