3. Силовой анализ механизмов

3.1. Общие сведения и определения. Силы, действующие в механизмах При проведении силового анализа решаются следующие основные задачи:

1. Определение реакций в кинематических парах механизмов, находящихся под действием заданных внешних сил. Эти реакции затем используются для расчёта звеньев и элементов кинематических пар (подшипников, например) на прочность, жёсткость, долговечность и т.д.

2. Определение уравновешивающей силы или уравновешивающего момента , приложенных к ведущему звену. Они уравновешивают внешние силы, приложенные к механизму. Эти величины нужны, например, для выбора двигателя, приводящего в движение данный механизм.

Силы, действующие в механизмах

Различают две большие группы сил:

движущие силы Р_дв. или моменты движущих сил М_дв., которые:

• совершают положительную работу;

• направлены в сторону скорости точки приложения силы или под острым углом к ней;

• задаются посредством механической характеристики двигателя;

силы сопротивленияР_С и их моменты М_С, которые

• совершают отрицательную работу;

• направлены противоположно скорости.

Они подразделяются на силы:

• полезного сопротивления Р_п.с. и моменты М_п.с.;

• вредного сопротивления:

а) трения в кинематических парах,

б) сопротивления среды,

в) внутреннего сопротивления (например, силы упругости звеньев).

Кроме того, существуют:

• силы веса 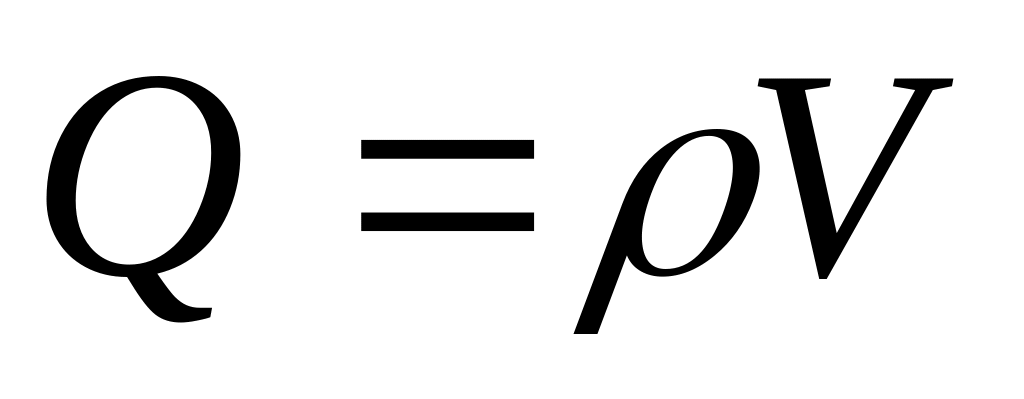, где  - плотность материала, V – объём звена детали;

• силы инерции ,

• моменты сил инерции , где

m_u, J_S – масса и массовый момент инерции звена; и - линейное и угловое ускорения;

– силы реакций в кинематических парах .

Силы инерции звеньев и моменты сил инерции.

Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллель­ное движение и имеющего плоскость симметрии, па­раллельную плоскости движения, могут быть сведены:

• к силе инерции , приложенной в центре масс S звена;

• к паре сил инерции, момент которых обозначим .

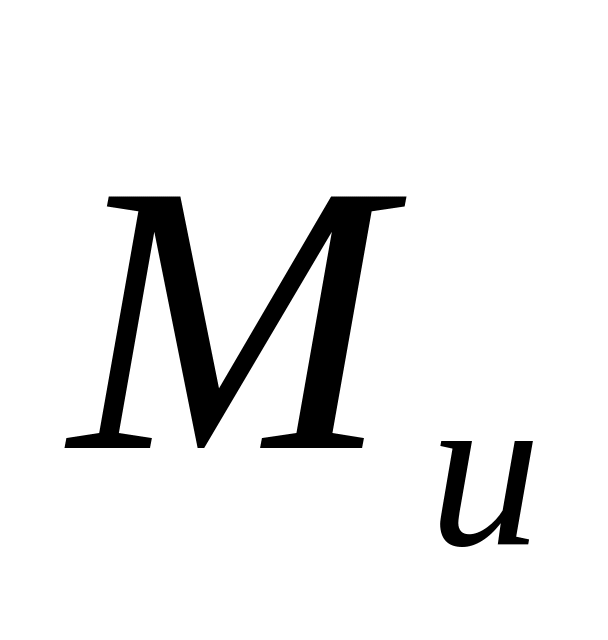– главный вектор сил инерции, который в дальнейшем будем называть силой инерции;

– главный момент сил инерции, который в дальнейшем будем называть моментом сил инерции, где m – масса звена, J_S – массовый момент инерции относительно центра масс, – ускорение центра масс, – угловое ускорение звена.

и направлены в стороны, противоположные ускорениям и .

Удобно для дальнейших расчётов заменить и одной силой. Для этого можно использовать 3 метода:

а) Метод замещающих точек: (см. /3/, стр. 252).

б) Перенос силы на плечо . При этом момент сил инерции заменяется парой сил с плечом h_u (рис. 3.1), причём одна из этой пары сил приложена к центру масс звена S и направлена противоположно преобразуемой силе , а другая сила смещена на плечо h_u и приложена к точке К. Здесь К – центр качания звена.

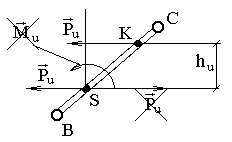
Рис. 3.1. Перенос силы на плечо при замене силы и момента одной силой

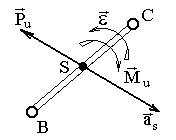
в) Определение центра качания звена через мгновенный центр ускорений (МЦУ).

При этом сила инерции переносится па­раллельно самой себе на расстояние (рис. 3.2), вычис­ленное по формуле

, мм.

Здесь – мгновенный центр ускорений звена, откладывается в сторону, являющуюся продолжением отрезка

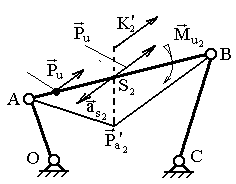
Рис. 3.2. Определение центра качания звена