
- •7. Вычислить выражения:
- •Вычислить:
- •Задание № 4-3.
- •Задание 5-4.
- •3. Вычислить определители:
- •Задание 6-3.
- •Задание № 73.
- •Задание № 8-5.
- •Задание 9-2.
- •2.Вычислить выражения:
- •Задание 101.
- •Ответы.
- •Задание № 13 1.
- •Ответы.
- •Задание № 143.
- •Ответы.
- •Задание № 15 4.
- •Ответы .
- •Задание № 16-2.
- •Ответы.
- •Задание № 17-1.
- •Задание № 18-5.
- •Ответы.
- •Задание № 19-4 .
- •Задание № 22-1.
- •Ответы.
- •Задание № 23 2.
- •Ответы.
- •Задание 243.
- •Ответы.
- •5. Доказательство.
- •25. Задания для самостоятельной работы.
- •Ответы.
- •26. Задачи и упражнения для самостоятельной работы
- •Ответы.
- •Задание № 274.
- •9.Применяя процесс ортогонализации, построить ортогональный базис оболочек векторов:
- •28. Задачи для самостоятельного решения
- •5. Написать уравнение плоскости, инвариантной относительно линейного преобразования , заданного в некотором ортонормированном базисе матрицей
- •9. Ответы к задачам для самостоятельного решения
- •29. Задачи для самостоятельного решения
- •Ответы к задачам для самостоятельного решения
- •30. Задачи для самостоятельного решения.
- •Ответы к задачам для самостоятельного решения.
Ответы .
1а. Нет. 1б. Да. 1в. Нет. 2а. Нет. 2б. Ком. 2в. Ком. 2г. Ком., ас. 3а. Да. 3б. Да. 3в. Да. . 3г. Да. 3д. Нет. 3е. Да при d = 1. 3ж. Нет. 3з. Нет. 3и. Да.
3к. Да.
Задание № 16-2.
1.Найти порядок элемента группы:
а) ![]() ;
б)
;
б)
![]()
2.Докажите, что группа корней 4-ой степени из 1 изоморфна аддитивной группе вычетов по модулю 4.
3.Какие из следующих числовых множеств образуют кольцо относительно обычных операций сложения и умножения:
а) множество nZ, nN , n > 1;
б) множество комплексных чисел вида x + yi, x, yQ ?
4.Какие из следующих множеств матриц образуют кольца:
а) 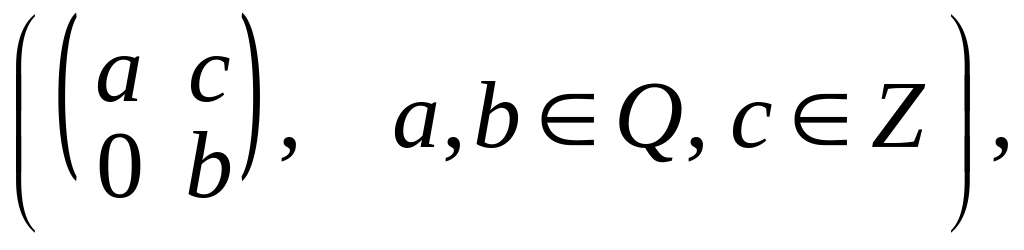 б)
б)  ;
;
в)  .
.
г) множество вещественных ортогональных матриц порядка n;
(А ортогональна, если АА'=A'A=E, A' транспонированная матрица).
д)
множество комплексных матриц вида
![]()
5.Доказать, что следующие множества являются полями:
а)
R ; б)
 .
.
6.Показать гомоморфизм колец
 при
отображении
при
отображении
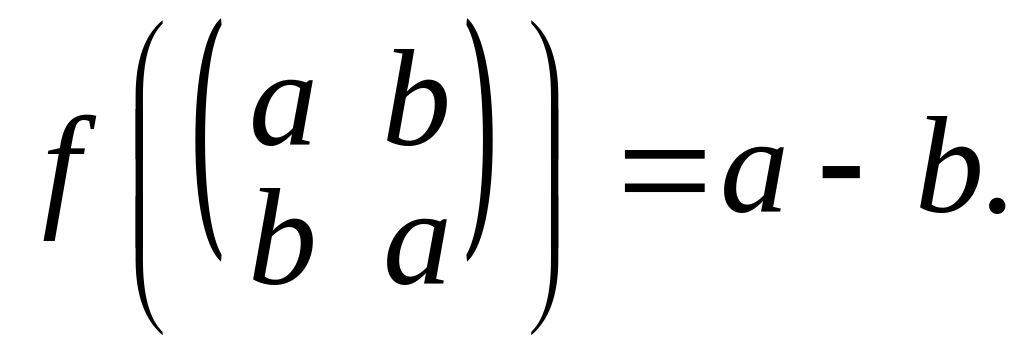
Ответы.
1а. 5; 1б. 2; 2. Док-во. 3а. Да. 3б. Да. 4а. Нет. 4б. Да. 4в. Да. 4г. Нет. 4д. Да.
Задание № 17-1.
1.Найти
обратную к квадратной матрице ![]() ,
где А, С - невырожденные матрицы.
,
где А, С - невырожденные матрицы.
2.Доказать, что всякая матрица может быть единственным образом представлена в виде суммы симметрической и кососимметрической матриц.
3.Найти все симметрические ортогональные и кососимметрические ортогональные матрицы порядка 2.
4.Решить уравнение АХ + Х + А = 0, где А - нильпотентная матрица.
5.Показать,
что операция транспонирования матрицы
обладает свойствами: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ,
где с
число, А, В
матрицы.
,
где с
число, А, В
матрицы.
6.Показать, что произведение двух симметрических матриц тогда и только тогда будет матрицей симметрической, когда данные матрицы перестановочные.
7.При каких условиях диагональная матрица является унитарной ?
8.Найти Аn для всех целых положительных чисел n:
а)
А =
![]() ;
б) А =
;
б) А =
![]()
Ответы.
1.
 8a.
8a. ![]()
2.
Доказательство. 8б. ![]()
5. Доказательство. 6. Доказательство. 7. Мод.диаг. эл.=1.
Задание № 18-5.
1.Выяснить, являются ли подобными между собой матрицы:
А
=
 В =
В =

2.Найти минимальный многочлен нильпотентной матрицы с показателем нильпотентности k.
3.Привести к нормальной диагональной форме путём элементарных преобразований следующие матрицы:
а)
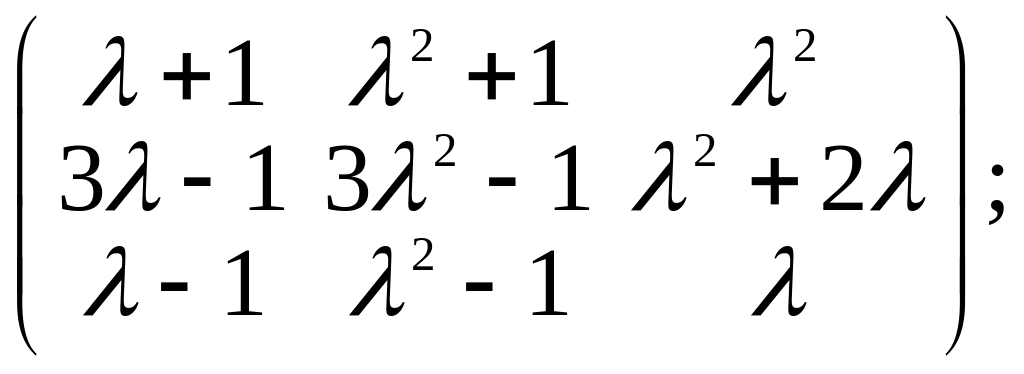 б)
б)
![]()
4.Привести к нормальной диагональной форме при помощи элементарных преобразований следующие матрицы:
а)
 б)
б)

Ответы.
1.
Да. 4а. 
2. tk.
3а.
 4б.
4б.
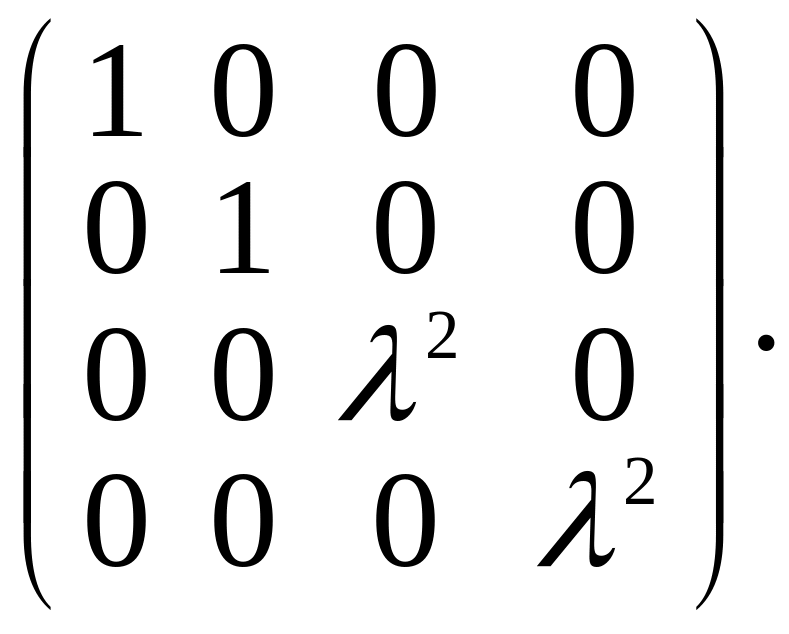
3б.

Задание № 19-4 .
1.Выяснить, являются ли подобными между собой матрицы:
А
=
 В =
В =

2.Найти минимальный многочлен матрицы

3.Привести к нормальной диагональной форме путём элементарных преобразований следующие матрицы:
а)
 б)
б) 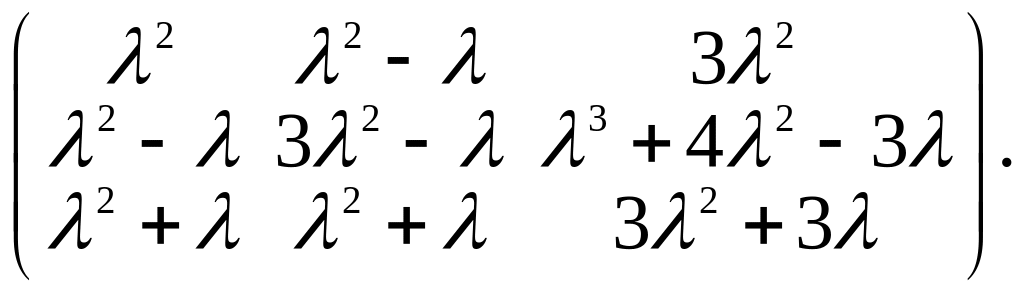
4.Привести к нормальной диагональной форме при помощи элементарных преобразований матрицу
 где
a,b,c,d
попарно взаимно простые многочлены.
где
a,b,c,d
попарно взаимно простые многочлены.
Ответы.
1.
Да. 4а.  где р =
где р =
 ,
,
2.
t2
5t + 6. ![]() их старш. коэф.
их старш. коэф.
3а.

3б.

ЗАДАНИЕ № 20-3.
Найти жорданову форму матриц:
1) ;
2)
;
2) ;
3)
;
3) ;
;
4) ;
5)
;
5) ;
6)
;
6) .
.
Ответы.
1) ;
2)
;
2)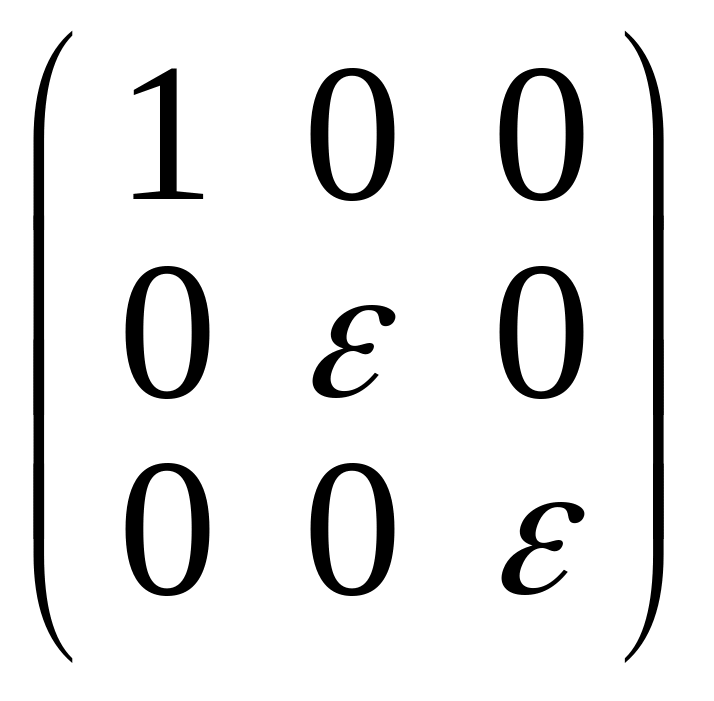 ;3)
;3) ;4)
;4) ;
5)
;
5) ;
6)
;
6) .
.

Задание № 212.
1.При каких значениях из линейной независимости системы век
торов {а1, а2} вытекает линейная независимость системы
{a1 + a2,} ?
2.Проверить, выполняются ли аксиомы векторного пространства
для множества всех векторов плоскости с операциями сложения и умножения на целые числа.
3.Является ли множество всех арифметических nмерных векторов
(x1, x2,..., xn) в F5 векторным пространством над полем F, если:
а) x1 = xn = 0, б) x1 x2 ...xn = 0 ?
4.Является ли векторным пространством над полем рациональных чисел множество чисел вида a + b , a, b рациональные числа.
5.Покажите,
что множество матриц вида ![]() с элементами из R
с элементами из R
является векторным пространством над полем R относительно обычных операций с матрицами.
6.При каких , , система векторов (1, , ), (0, 1, ), (0, 0, 1) образует базис арифметического векторного пространства над полем R ?
Ответы 1 Док-во.
2 Нет.
3а Да.
3б Да.
4 Да.
5 Док-во.
6 При любых.
