
- •2) Дискретные,
- •3) Дискретно-непрерывные,
- •4) Непрерывно-дискретные.
- •3.1. Математические модели непрерывных моделей каналов связи
- •3.2. Математические модели дискретного канала
- •Дискретный симметричный канал без памяти
- •Двоичный симметричный канал со стиранием
- •Канал с памятью
- •3.3 Методы повышения качества передачи информации и снижения уровня мешающих воздействий, применяемые в итс
- •6.Охарактеризуйте цифровые методы преобразования речевых сигналов в информационно-телекоммуникационных системах с позиций уменьшения объема их битового представления.
- •8. Охарактеризуйте роль и виды модуляции в системах связи.
- •Угловая модуляция (ум).
- •10.Охарактеризуйте существующие методы уплотнения каналов, обоснуйте процесс выбора структуры приемо-передающего тракта и приведите примеры их технической реализации в реальных системах связи.
- •10.1 Уплотнение с частотным разделением (fdm)
- •Множественный доступ с частотным разделением в спутниковых системах (fdma)
- •10.2 Уплотнение(tdm)/множественный доступ с временным разделением(tdmа).
- •10.3 Уплотнение (сdm)/множественный доступ с кодовым разделением(сdmа).
3.2. Математические модели дискретного канала
Переходя к моделям дискретного канала, полезно напомнить, что в нем всегда содержится непрерывный канал, а также модем. Последний можно рассматривать как устройство, преобразующее непрерывный канал в дискретный. Поэтому, в принципе, можно вывести математическую модель дискретного канала из моделей непрерывного канала и модема. Такой подход часто является плодотворным, однако он приводит к довольно сложным моделям, анализ которых не входит в программу читаемой дисциплины. В данной лекции рассмотрим простые модели дискретного канала, при построении которых свойства непрерывного канала и модема не учитываются. Следует, однако, помнить, что при проектировании системы связи имеется возможность варьировать в широких пределах модель дискретного канала при заданной модели непрерывного путем изменения модема.
Модель дискретного канала содержит задание множества возможных сигналов на его входе и распределение условных вероятностей выходного сигналу при заданном входном. Здесь входным и выходным сигналами являются последовательности кодовых символов. Поэтому для определения возможных входных сигналов достаточно указать число т различных символов (основание кода), а также длительность Т передачи каждого символа. Будем считать, что значение Т одинаково для всех символов, что выполняется в большинстве современных каналов.
В
общем случае для любого п
(количество символов в кодовом слове)
должна быть указана вероятность
того, что при подаче на вход канала любой
заданной последовательности B[n]
кодовых символов на выходе появится
некоторая реализация случайной
последовательности
![]() .
Кодовые символы обозначим числами
от о
до m-1,
что позволит производить над ними
арифметические операции. При этом все
последовательности (векторы),
количество которых равно тп,
образуют тп
- мерное
конечное векторное пространство, если
«сложение» понимать как поразрядное
суммирование по модулю m
и аналогично определить умножение на
скаляр (целое число). В случае, когда
m=2,
векторное пространство называется
пространством Хемминга. Скалярное
произведение здесь имеет вид
.
Кодовые символы обозначим числами
от о
до m-1,
что позволит производить над ними
арифметические операции. При этом все
последовательности (векторы),
количество которых равно тп,
образуют тп
- мерное
конечное векторное пространство, если
«сложение» понимать как поразрядное
суммирование по модулю m
и аналогично определить умножение на
скаляр (целое число). В случае, когда
m=2,
векторное пространство называется
пространством Хемминга. Скалярное
произведение здесь имеет вид
![]()
где
![]() -
знак суммирования в обычном смысле.
-
знак суммирования в обычном смысле.
Норма (длина вектора) двоичного вектора представлена выражением:
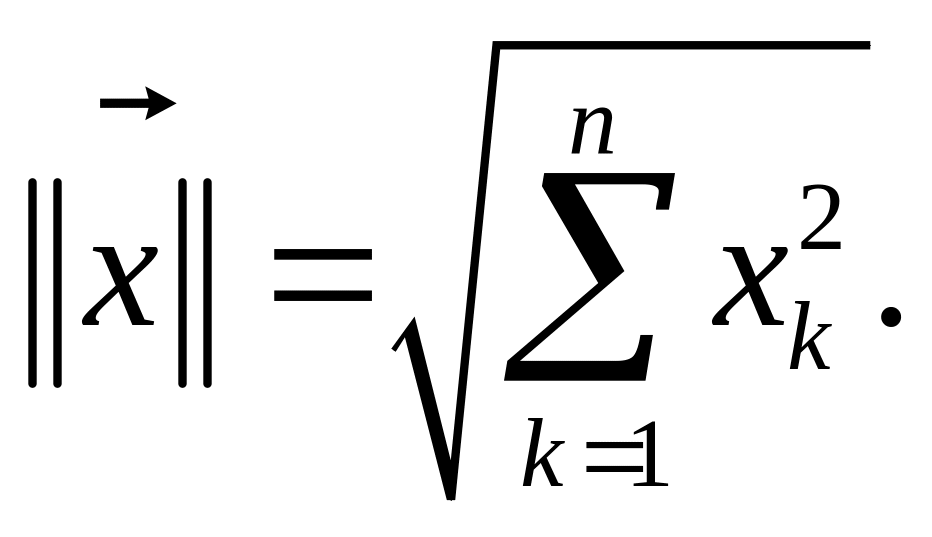
и определяется количеством содержащихся в нем единиц. Норму такого вектора называют весом вектора и обозначают обычно ω. Расстояние между векторами в пространстве Хемминга равно норме их разности:
![]()
Здесь
знак
![]() означает сложение по модулю 2 (mod 2): 0
0 = 0,
означает сложение по модулю 2 (mod 2): 0
0 = 0,
1 1 = 0, 0 1 = 1, 1 0 = 1. Заметим, что сложение и вычитание по mod 2 эквивалентны.
Пример: х = 1001011
y = 0101101
х у = 1100110
В пространстве Хемминга расстояние между двоичными векторами равно числу позиций (элементов), которыми различаются эти вектора.
В
данном примере
![]()
Введем понятие вектора ошибок, под которым будем понимать поэлементную разность между принятым и переданным векторами. Иными словами, при передаче по дискретному каналу вектор сигнала складывается с вектором ошибок:
![]()
где Е [п] — вектор ошибок, который в дискретном канале играет такую же роль, как и помеха в непрерывном канале.
В двоичном канале при т=2 смысл вектора ошибок понимается наиболее просто. Каждая единица в этом векторе указывает на то, что именно на данной позиции в векторе сигнала произошла ошибка. Нулевая позиция в векторе ошибок свидетельствует о правильном приеме соответствующего элемента сигнала. (Необходимо отметить, что аналогичные выкладки были использованы при рассмотрении материала по кодированию) Образно говоря, переход от непрерывного канала к дискретному соответствует преобразованию любой помехи в поток ошибок. При этом различные модели дискретного канала будут описываться разными распределениями вероятностей векторов ошибок.
Рассмотрим наиболее часто встречающиеся простейшие модели дискретных каналов.
