МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ

ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ П.А. СОЛОВЬЕВА

КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ

	УТВЕРЖДЕНО на заседании методического семинара кафедры ОиТФ « » 1999 г. Зав.каф. Пиралишвили Ш.А.

Лаборатория «Физические основы механики»

ЛАБОРАТОРНАЯ РАБОТА № ФМ-5 «А»

ИССЛЕДОВАНИЕ УПРУГОГО УДАРА

	Методическое руководство подготовлено: к.т.н., доцент Суворовой З. В.
	Рецензент: доц. Конюхов Б.М.

Рыбинск 1999

ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ

Перед включением электроприборов проверить целостность шнуров питания и вилки.

Порядок включения установки: вилка «Сеть», тумблер «Сеть», необходимые переключатели режимов.

Порядок выключения: вывести все переключатели в нулевое положение, выключить тумблер «Сеть», выключить вилку.

Установка ФП 109М подключена к гнездам источника питания 6В. Категорически запрещено переключать ее на другое напряжение. В случае выхода из строя приборов из-за халатного отношения, студент несет материальную ответственность за восстановление прибора. Все необходимые переключения приборов описаны в разделе «Порядок выполнения работы».

ЦЕЛЬ РАБОТЫ: изучение законов сохранения импульса и механической энергии. Определение времени соударения.

1. Краткие теоретические сведения

Ударом называют кратковременное взаимодействие тел. При ударе тела деформируются, и в месте контакта возникает весьма значительные ударные силы F_уд, величина которых соответствует ( ) Н. Для системы соударяющихся тел эти силы являются внутренними и не изменяют общего импульса системы, т.е. такая система является замкнутой.

Процесс соударения можно разделить на две фазы:

– от момента соприкосновения до момента прекращения сближения тел.

В течение этой фазы часть кинетической энергии тел переходит в потенциальную энергию деформации;

– обратный переход потенциальной энергии деформации в кинетическую энергию тел.

Удар называется центральным, если в момент удара центры инерции сталкивающихся тел находятся на одной прямой. Если скорости тел направлены по одной прямой, то удар называется прямым.

Различают два предельных случая удара – абсолютно упругий и абсолютно неупругий.

Удар называется абсолютно упругим, если механическая энергия тел не переходит в другие, немеханические, виды энергии. В этом случае кинетическая энергия соударяющихся тел переходит полностью или частично в энергию упругой деформации, после чего тела возвращаются к первоначальной форме, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются. При абсолютно упругом ударе выполняются законы сохранения механической энергии и импульса.

Абсолютно неупругий удар характеризуется тем, что кинетическая энергия тел полностью или частично переходит во внутреннюю энергию. После удара столкнувшиеся тела движутся вместе с одинаковой скоростью.

а) б)

Рис. 1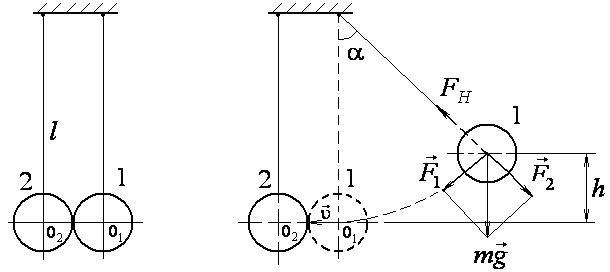

При таком ударе выполняется закон сохранения импульса, однако закон сохранения механической энергии не выполняется, т.к. часть механической энергии переходит во внутреннюю. В этом случае выполняется более общий закон сохранения энергии – механической и внутренней. Рассмотрим соударение двух шаров массами и , подвешенных на нитях длины . Удар можно считать прямым центральным, если длина нити много больше размеров шаров ( ). В этом случае скорости шаров непосредственно до и после удара направлены по одной прямой (ось скоростей). Если размеры шаров одинаковы, и нити, на которых висят шары имеют одинаковую длину, то центры масс шаров лежат на оси скоростей, и удар является прямым (рис. 1а).

Для сообщения шару 1 скорости , его отклоняют на угол (рис. 1б). При этом центр масс шара поднимается на высоту относительно уровня положения равновесия О₁О₂, т.е. шар 1 приобретает потенциальную энергию . Шар отпускают, и он начинает двигаться под действием двух сил – силы натяжения нити и силы тяжести . Равнодействующая этих сил

направлена по касательной к дуге окружности, по которой движется тело к положению равновесия (к точке О₁). При движении тела его потенциальная энергия переходит в кинетическую, и для точки О₁ можно записать

.

Из рисунка 1б видно, что , поэтому

. (1)

Рассмотрим абсолютно упругий удар. При таком ударе выполняется два закона сохранения – закон сохранения импульса и закон сохранения кинетической энергии (рис. 2).

а) до удара

б) после удара

Рис. 2

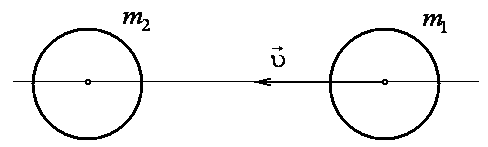
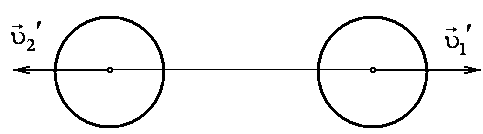
Обозначим скорости шаров после удара и (рис.2).

Запишем уравнение сохранения импульса и энергии:

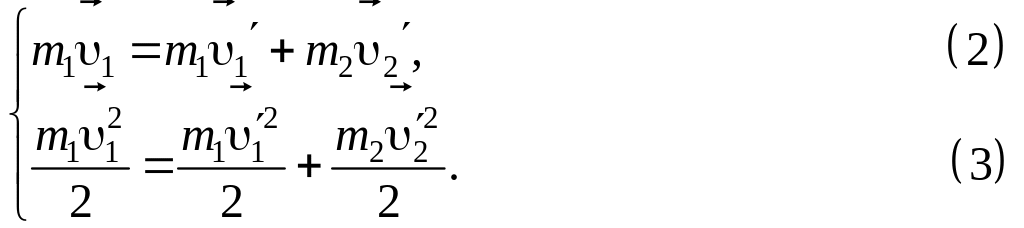
Преобразуем (3) следующим образом:

или

(4)

Из соображений симметрии можно утверждать, что скорости шаров после удара будут направлены вдоль прямой О₁О₂. Следовательно, все векторы в выражении (4) коллинеарны. Выражение (2) перепишем в виде:

Сравнивая его с выражением (4), получаем:

(5)

Умножим равенство (5) на и вычислим его из (2), имеем:

Отсюда

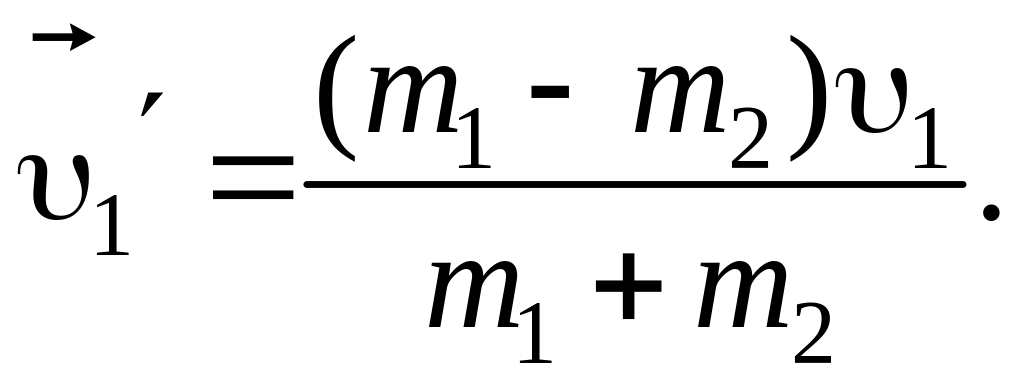(6)

Умножив (5) на и складывая результат с равенством (2), получаем:

или

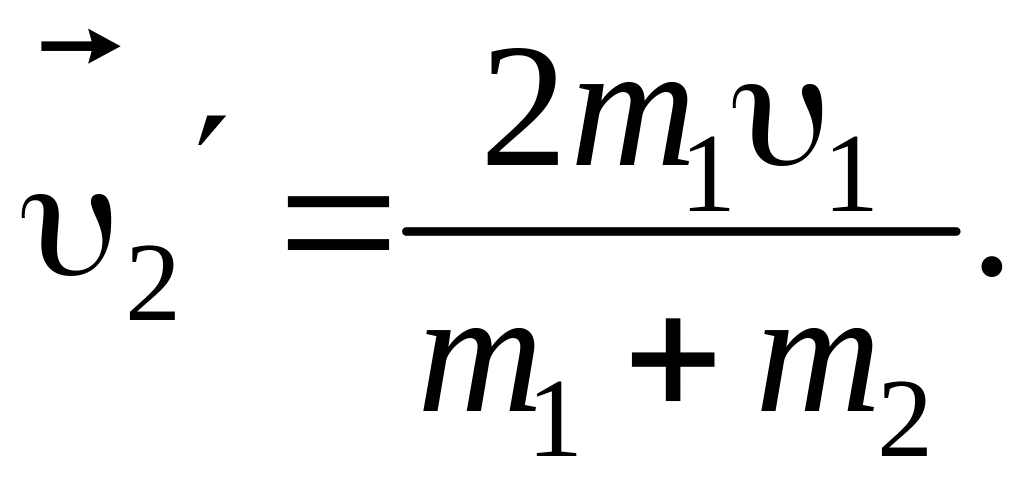
Спроектировав выражение (6) и (7) на направление вектора , получаем

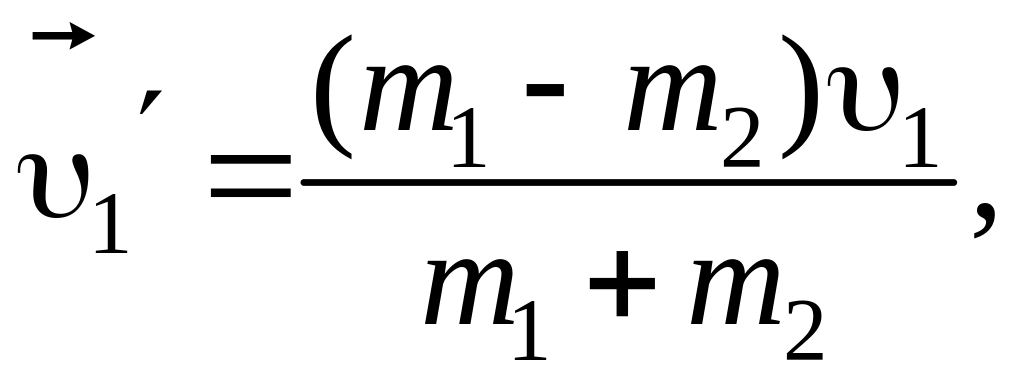
Если массы шаров одинаковы, , для скоростей после удара имеет:

,

– шары 1 и 2 меняются состояниями (рис. 3).

Рис. 3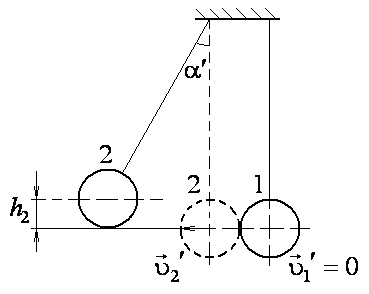

Шар 2 за счет свой кинетической энергии поднимается на высоту :

,

при этом

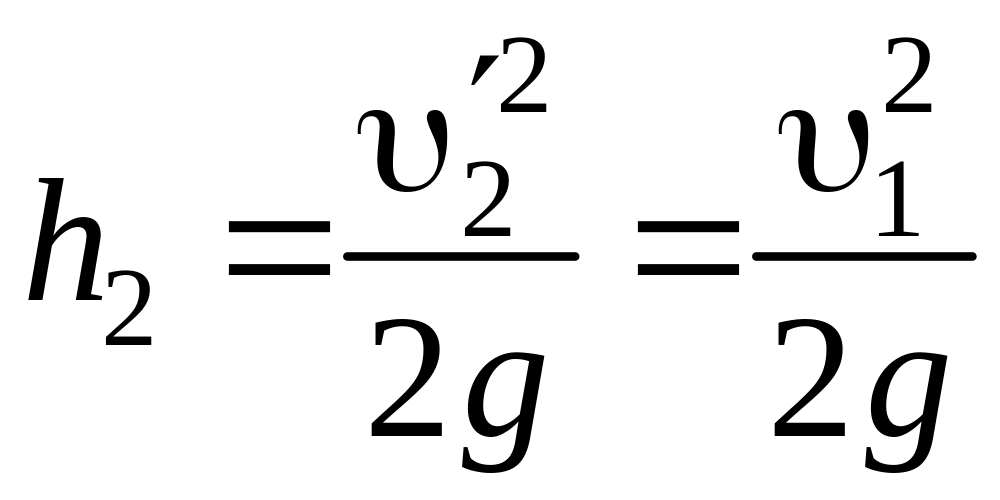
Подставив значение из формулы 1, имеем:

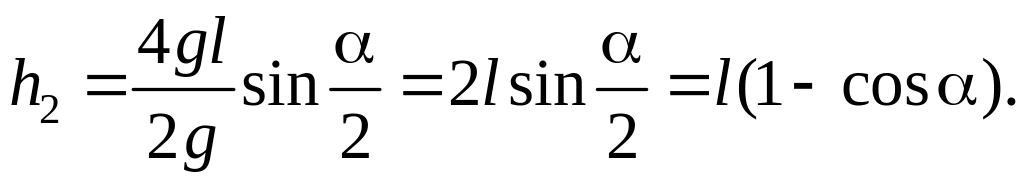
Из рис. 3 видно, что Таким образом, .