МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ

ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ П.А. СОЛОВЬЕВА

КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ

	УТВЕРЖДЕНО на заседании методического семинара кафедры ОиТФ « » 1995 г. Зав.каф. Пиралишвили Ш.А.

Лаборатория «Физические основы механики»

ЛАБОРАТОРНАЯ РАБОТА № ФМ-5

ОПРЕДЕЛЕНИЕ ВРЕМЕНИ И

	Методическое руководство подготовлено:
	доц. Суворова З. В. инженер Гусев Е. В.
	Рецензент: Бутина И. И.
	­­­­­­­­­

ЭНЕРГИИ УДАРА

Рыбинск 1995

ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ:

Перед включением электроприборов проверить целостность шнуров питания, вилки и заземление.

Порядок включения установки: вилка «Сеть», тумблер «Сеть», необходимые переключатели режимов.

Порядок выключения: вывести все переключатели в нулевое положение, выключить тумблер «Сеть», выключить вилку.

Установка ФП109М подключена к гнездам источника питания 6 В. Категорически запрещено переключать ее на другое напряжение. В случае выхода из строя приборов из-за халатного отношения, студент несет материальную ответственность за восстановление прибора. Все необходимые переключения приборов описаны в разделе «Порядок выполнения работы».

ЦЕЛЬ РАБОТЫ: изучение перераспределения энергии соударяющихся тел, определение времени удара.

ПРИБОРЫ И ОБОРУДОВАНИЕ: лабораторная установка ФП109М, источник питания УИП-2, вольтметр ВК7 -15.

1. Краткие теоретические сведения

Ударом называют кратковременное взаимодействие тел. При ударе тела деформируются, и в месте контакта возникают весьма значительные ударные силы F_уд, величина которых соответствует 10⁴ –10⁶ Н. Для системы соударяющихся тел эти силы являются внутренними и не изменяют общего импульса системы, т.е. такая система является замкнутой.

Процесс соударения можно разделить на две фазы:

- от момента соприкосновения до момента прекращения сближения тел.

В течение этой фазы часть кинетической энергии тел переходит в потенциальную энергию деформации;

- обратный переход потенциальной энергии деформации в кинетическую энергию тел.

Удар называется центральным, если в момент удара центры инерции сталкивающихся тел находятся на одной прямой. Если скорости тел направлены по одной прямой, то удар называется прямым.

Различают два предельных случая удара – абсолютно упругий и абсолютно неупругий.

Удар называется абсолютно упругим, если механическая энергия тел не переходит в другие, немеханические, виды энергии. В этом случае кинетическая энергия соударяющихся тел переходит полностью или частично в энергию упругой деформации, после чего тела возвращаются к первоначальной форме, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются. При абсолютно упругом ударе выполняются законы сохранения механической энергии и импульса.

Абсолютно неупругий удар характеризуется тем, что кинетическая энергия тел полностью или частично переходит во внутреннюю энергию. После удара столкнувшиеся тела движутся вместе с одинаковой скоростью.

При таком ударе выполняется закон сохранения импульса, однако закон сохранения механической энергии не выполняется, т.к. часть механической энергии переходит во внутреннюю. В этом случае выполняется более общий закон сохранения энергии – механической и внутренней. В реальных ситуациях всегда имеет место некоторая комбинация обоих предельных случаев.

Рис. 1

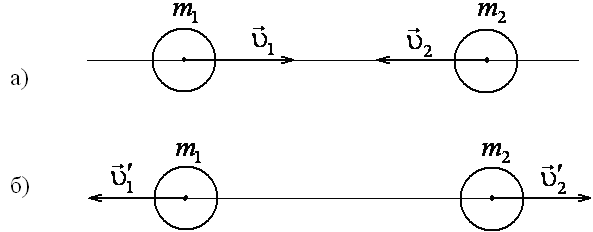
Рассмотрим упругий центральный прямой удар двух шаров с массами и и скоростями и соответственно (рис.1а).

Согласно закону сохранения импульса, имеем:

(1)

где и – скорости шаров после соударения (рис.1б).

Запишем выражение закона сохранения энергии:

(2)

Из (1) и (2) имеем:

. (3)

Рассмотрим упругий удар шара массой о неподвижную стенку. Масса стенки >> , и поэтому

Тогда

При покоящейся стенке и поэтому

(4)

– скорость стенки остается неизменной, скорость же шара меняет свое направление на противоположное.

Для характеристики удара вводят понятие коэффициента восстановления относительной скорости при ударе k:

(5)

где относительная скорость шаров до удара,

относительная скорость шаров после удара.

Коэффициент восстановления принимает значения в интервале

В случае прямого центрального удара движение тел происходит по прямой x, за начало отсчета примем центр инерции второго тела. Первое тело движется в этой системе отсчета со скоростью , его импульс равен

после удара полный импульс системы равен

Таким образом, коэффициент восстановления показывает, какая часть импульса первого тела, измеряемого в системе центра масс второго тела, сохраняется в результате удара.

Его удар абсолютно неупругий, то после удара оба тела движутся вместе и поэтому

Возведем правую часть выражения (5) в квадрат и извлечем квадратный корень:

(6)

Квадрат коэффициента восстановления показывает, какая часть кинетической энергии первого тела, измеренной в системе центра масс второго тела, теряется в результате удара.

Для абсолютно упругого удара выполняются законы сохранения импульса и энергии , в выбранной системе отсчета они имеют вид:

(7)

где – скорость центра масс второго тела после удара, измеренная в системе центра масс этого тела до удара.

Решая совместно уравнения (7), получим, что т.е. в случае абсолютно упругого удара относительный импульс первого тела, сохраняется, хотя сам центр масс второго тела меняет свое положение в пространстве.

Рис. 2

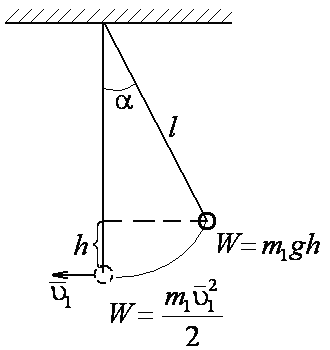
В лабораторной установке используется шар, подвешенный на нерастяжимой нити длины l (рис.2). Потенциальную энергию шара в положении равновесия примем равной нулю. За начало отсчета высоты примем высоту, на которой находится центр масс шара в этом положении. Тогда, при отклонении шара на угол , ему сообщается потенциальная энергия где масса шара. Если шар отпустить, он будет двигаться к положению равновесия, и его потенциальная энергия переходит в кинетическую. В положении равновесия вся потенциальная энергия шара переходит в кинетическую, т.е.

где скорость шара при прохождении положения равновесия.

Из рисунка 2 видно, что

тогда

(8)

После удара о стенку шар отскочил на угол его скорость равна:

  (9)

Коэффициент восстановления относительной скорости шара равен:

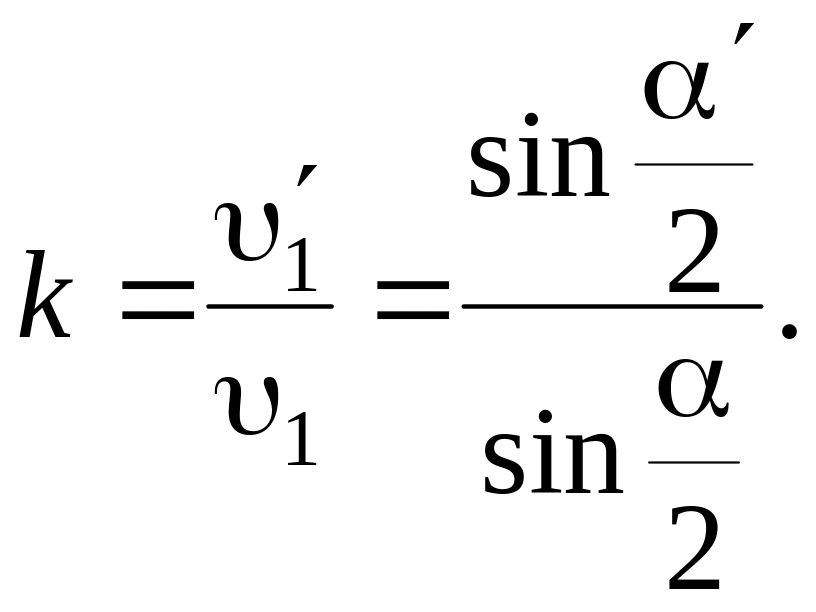(10)