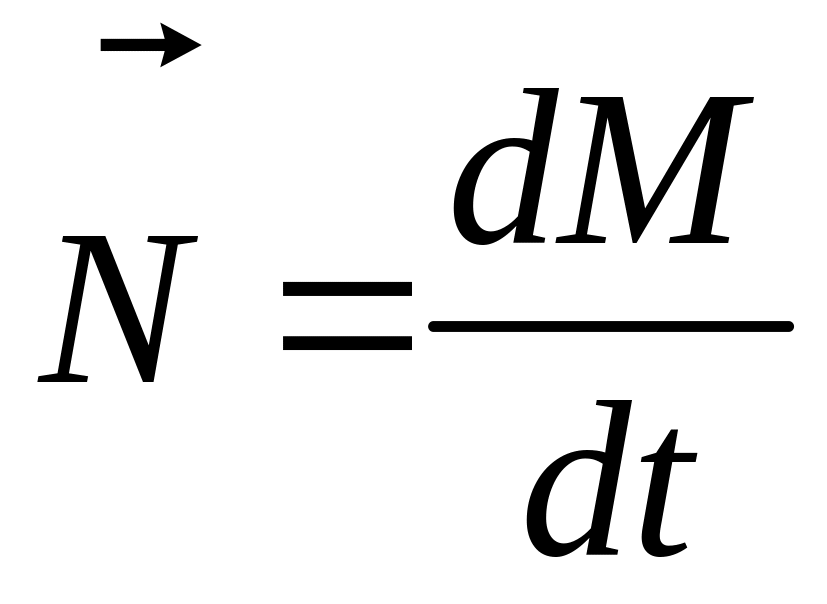1.5 Момент импульса и закон его сохранения

Моментом импульса материальной точки А относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением:

(1.5.1)

где – радиус-вектор, проведённый из точки О в точку А; – импульс материальной точки (рис. 1.5.1); – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Рис. 1.5.1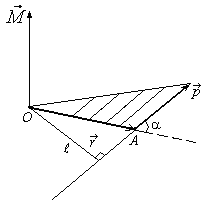

Модуль вектора момента импульса

,

где – угол между векторами и , – плечо вектора относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси. Значение момента импульса не зависит от положения точки О на оси z.

При вращении абсолютно твёрдого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, т.е. радиус является плечом вектора . Поэтому можно записать, что момент импульса отдельной частицы

и направлен по оси в сторону, определяемую правилом правого винта.

Момент импульса твёрдого тела относительно оси есть сумма моментов импульсов отдельных частиц:

.

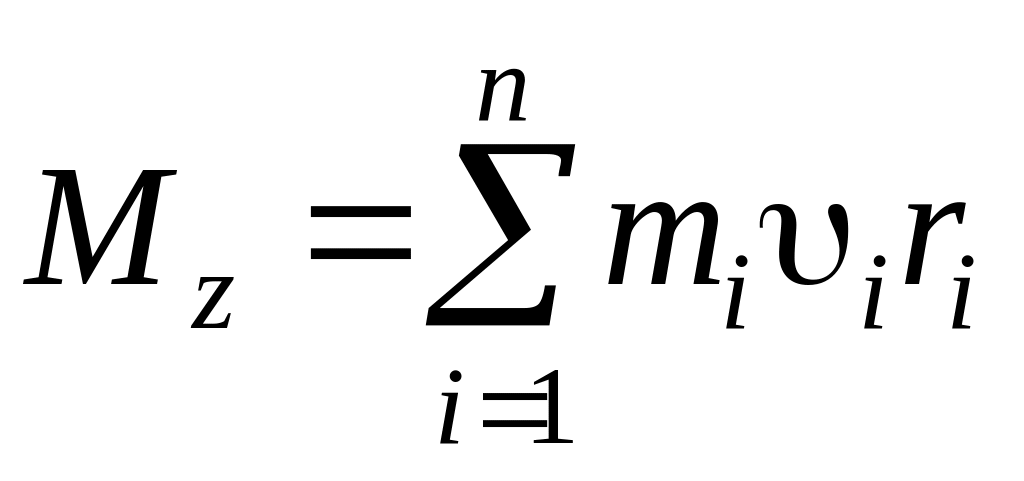Используя формулу , получим

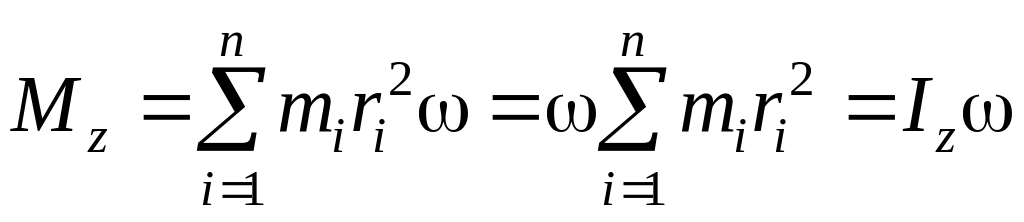, т.е. . (1.5.2) Таким образом, момент импульса твёрдого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцируем уравнение (1.5.2) по времени:

, т.е. (1.5.3)

Это выражение – ещё одна форма уравнения (закона) динамики вращательного движения твёрдого тела относительно неподвижной оси: производная момента импульса твёрдого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство .

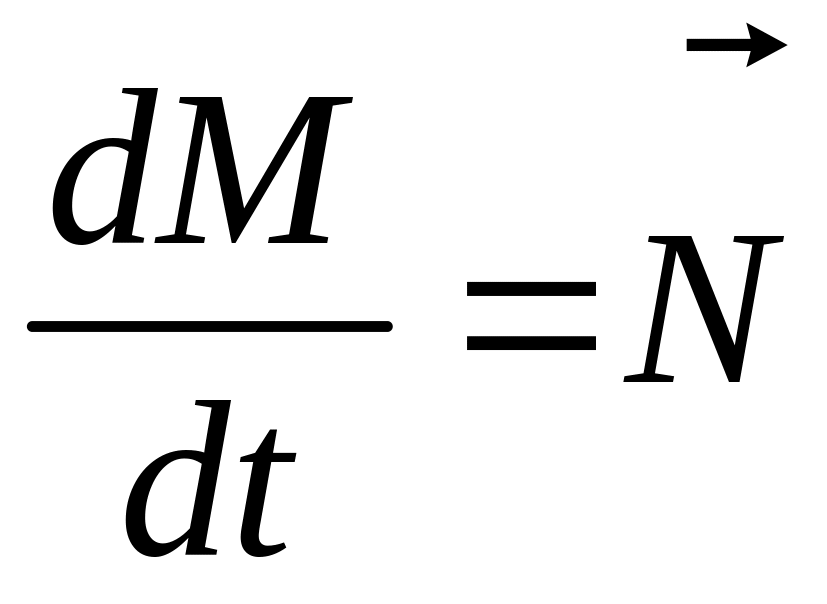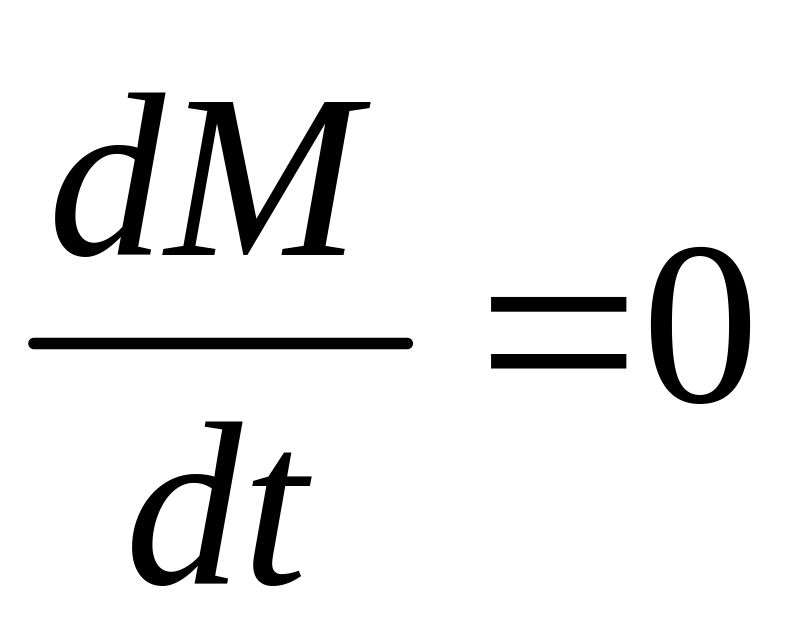В замкнутой системе момент внешних сил и , откуда

. (1.5.4)

Выражение (1.5.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется.

Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (таблица 1.5.1).

Таблица 1.5.1

Поступательное движение		Вращательное движение			Функциональная зависимость
Линейное перемещение	S	Угловое перемещение
Линейная скорость		Угловая скорость
Линейное ускорение		Угловое ускорение
Масса	m	Момент инерции		I	(для материальной точки)
Сила		Момент силы
Импульс		Момент импульса
Основное уравнение динамики
Работа			Работа вращения
Кинетическая энергия			Кинетическая энергия вращения
Закон сохранения импульса			Закон сохранения момента импульса