1.2 Момент инерции

Моментом инерции системы (тела) относительно оси вращения называется скалярная физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

.

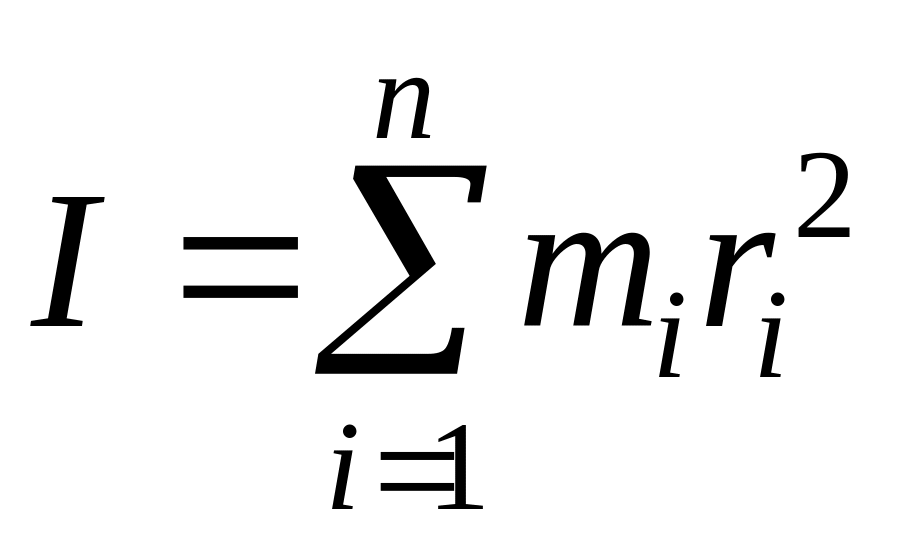В случае непрерывного распределения масс эта сумма сводится к интегралу:

,

где интегрирование производится по всему объёму тела. Величина в этом случае есть функция положения точки с координатами x, y, z.

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела I относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс C тела, сложенному с произведением массы m тела на квадрат расстояния d между осями:

.

В таблице 1.2.1 приведены значения моментов инерции для некоторых тел (тела считаются однородными, m – масса тела).

Таблица 1.2.1

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр, обруч радиусом R	Ось симметрии
Сплошной цилиндр (диск) радиусом R	Ось симметрии
Прямой тонкий стержень длиной	Ось перпендикулярна стержню и проходит через его середину
Прямой тонкий стержень длиной	Ось перпендикулярна стержню и проходит через его конец
Шар радиусом R	Ось проходит через центр шара

Если тело имеет сложную форму, и теоретически определить момент инерции его сложно, прибегают к экспериментальным методам определения момента инерции.

1.3 Кинетическая энергия вращения

Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1.3.1). Мысленно разобьём это тело на маленькие объёмы с элементарными массами , ,..., , находящиеся на расстоянии , ,..., от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы массами опишут окружности различных радиусов и имеют различные линейные скорости . Но так как мы рассматриваем абсолютно твёрдое тело, то угловая скорость вращения этих объёмов одинакова:

(1.3.1)

Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов:

.

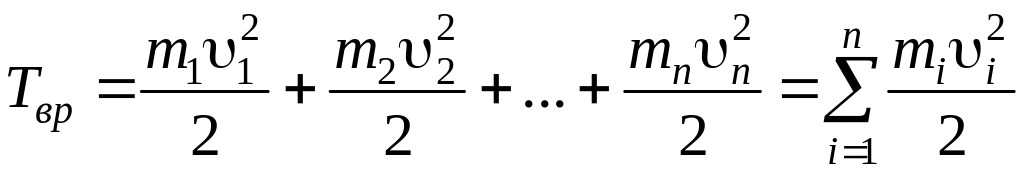Используя выражение (1.3.1), получим:

Рис. 1.3.1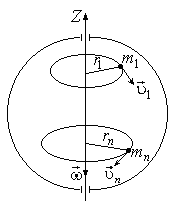

(1.3.2)

где – момент инерции тела относительно оси z.

Из сравнения формулы (1.3.2) с выражением для кинетической энергии тела, движущегося поступательно 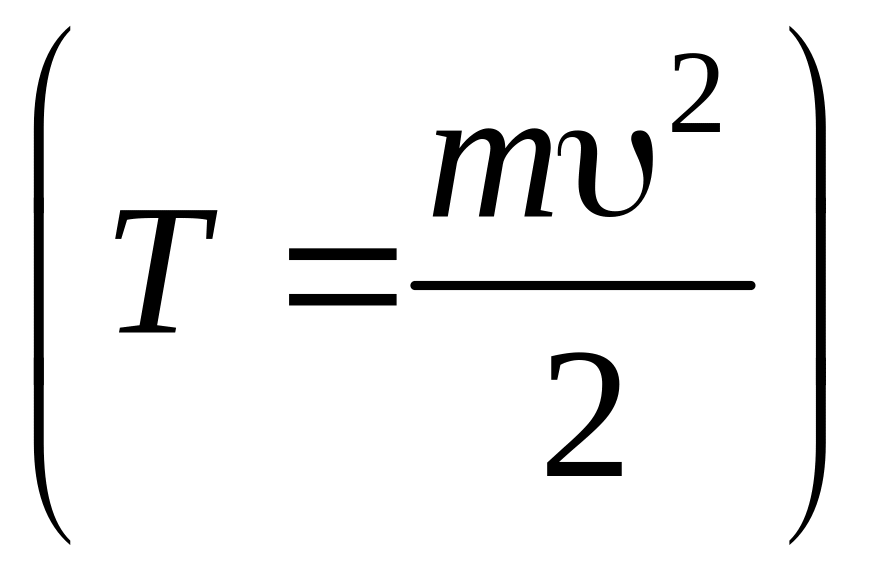, следует, что момент инерции I вращательного движения – мера инертности тела во вращательном движении, т.е. является вращательным аналогом массы.

1.4 Момент силы. Уравнение динамики

ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА

Моментом силы относительно неподвижной точки O называется векторная физическая величина, определяемая векторным произведением радиус-вектора , проведённого из точки O в точку A приложения силы, на силу (рис.1.4.1):

(1.4.1)

Здесь – псевдовектор, его направление совпадает с направлением движения правого винта при его вращении от к .

Рис. 1.4.1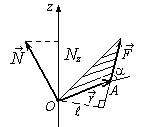

Модуль момента силы

,

где – угол между и , – кратчайшее расстояние между линией действия силы и точкой О – плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента силы, определённого относительно произвольной точки O данной оси z (рис. 1.4.1).

Работа при вращении тела равна произведению момента действующей силы на угол поворота:

.

С другой стороны эта работа идёт на увеличение его кинетической энергии:

, но

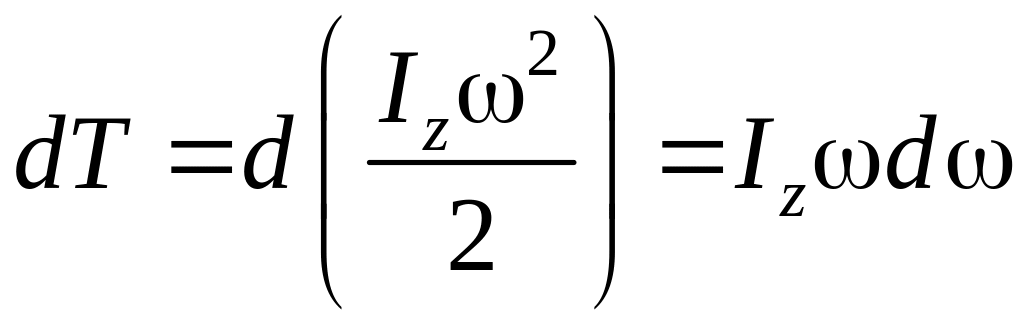, поэтому

, или .

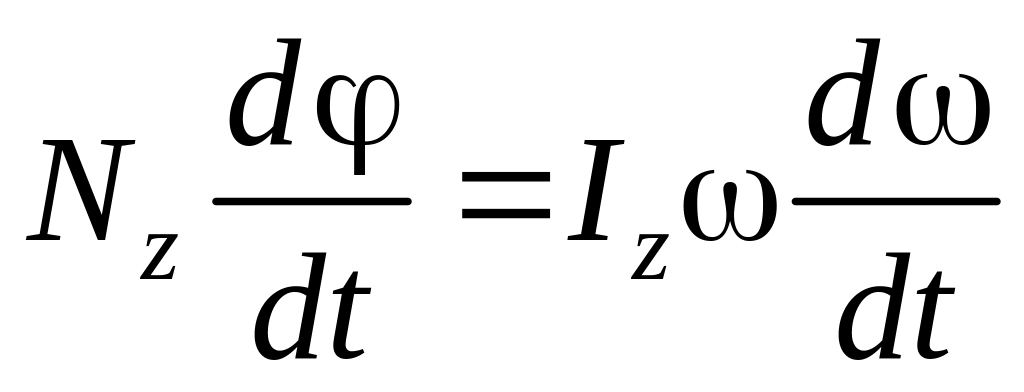Учитывая, что , получим

(1.4.2)

Получили уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.

Можно показать, что если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство:

,

где I – главный момент инерции тела (момент инерции относительно главной оси).