
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ
ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ П.А. СОЛОВЬЕВА
КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ
|
УТВЕРЖДЕНО на заседании методического семинара кафедры ОиТФ « » 1995г.
Зав.каф. Пиралишвили Ш.А. |
|
|
Лаборатория «Физические основы механики»
ЛАБОРАТОРНАЯ РАБОТА № ФМ-6
ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛА
ОТНОСИТЕЛЬНО ГЛАВНЫХ ОСЕЙ
ИНЕРЦИИ
|
Составитель: к.т.н., доцент |
|
___________ Суворова З. В. |
|
Рецензент: к. ф-м. н. доцент _____________Шувалов В. В. |
Рыбинск 1995
ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ:
Вы работаете с дорогостоящим оборудованием. Все манипуляции с установкой, не оговоренные в пункте «Порядок выполнения работы», категорически запрещены!
Установка находится под напряжением. Будьте внимательны и осторожны при выполнении работы!
При установке исследуемого тела в рамку избегайте соскальзывания и падения его на прибор.
ПОМНИТЕ, за порчу лабораторного оборудования ВЫ несете персональную ответственность.
ЦЕЛЬ РАБОТЫ: определение периодов колебаний и моментов инерции тел относительно главных осей инерции.
1. Краткие теоретические сведения
Моментом инерции тела относительно некоторой оси в физике называют величину, равную сумме произведений элементарных масс, из которых состоит тело, на квадраты их расстояний до оси:
![]()
Проекция момента импульса тела на ось вращения и угловую скорость связаны соотношением:
![]()
Если однородное симметрическое тело вращается вокруг вертикальной оси, то силы бокового давления подшипников на ось не возникают (рис.1).
Рис. 1
Для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр масс тела оси, которые могут служить свободными осями. Они называются главными осями тела.
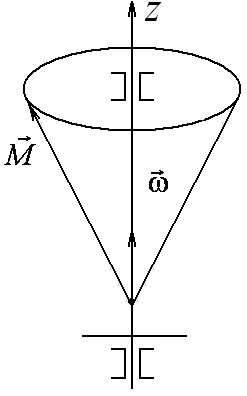
У однородного параллелепипеда главными осями инерции будут оси О1О1, О2О2, О3О3, проходящие через центры противолежащих точек (рис.2).
Рис. 2
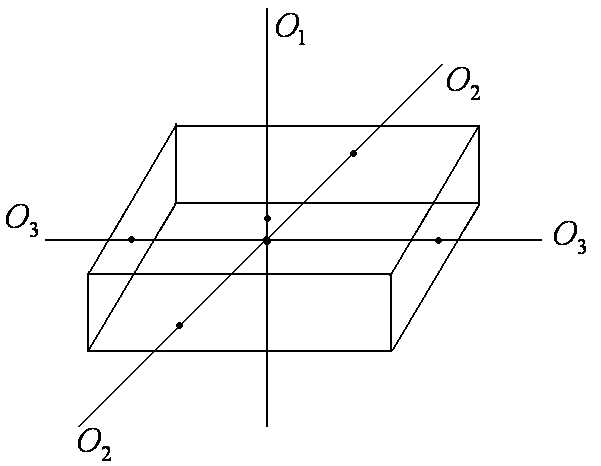
Рис. 3
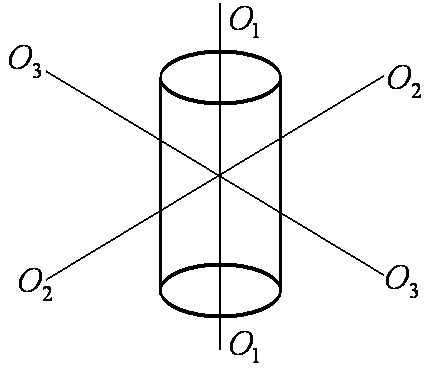
У тела с центральной симметрией (шар), главными осями инерции являются три любые взаимно перпендикулярные оси, проходящие через центр масс, где ни одна из главных осей не фиксирована (рис.4).
Рис. 4
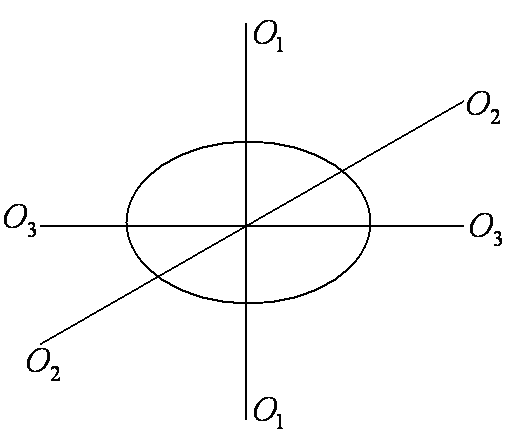
В общем случае эти моменты различны:
![]()
Для однородного тела с осевой симметрией два главных момента инерции одинаковы, а третий отличен от них:
![]()
Для однородного тела с центральной симметрией все три главных момента инерции одинаковы:
![]()
Равными значениями главных моментов инерции обладает не только шар, но и однородный куб. Такие тела называются шаровыми волчками. Для них характерно такое распределение массы внутри тела, что любая ось, проходящая через центр масс, обладает свойствами свободной оси, т.е. ни одна из главных осей инерции не фиксирована. Все шаровые волчки ведут себя при вращении в идентичных условиях одинаковым образом.
Тела, для которых
![]() ,
ведут себя как однородные тела вращения,
их называют симметричными волчками.
,
ведут себя как однородные тела вращения,
их называют симметричными волчками.
Если тело вращается без воздействия извне, то устойчивым оказывается только вращение вокруг главных осей, соответствующих максимальному и минимальному значениям момента инерции. Вращение же вокруг оси, соответствующей промежуточному по величине моменту, будет неустойчивым, это означает, что силы, возникающие при дальнейшем отклонении оси вращения от этой главной оси, действуют в таком направлении, что величина этого отклонения возрастает. При отклонении вращения от устойчивой оси под действием возникающих при этом сил, тело возвращается к вращению вокруг соответствующей главной оси.
В этом можно убедиться, подбросив коробок и заставив его вращаться. Такое тело будет вращаться устойчиво только относительно осей, проходящих через наибольшую и наименьшую грани. Вращения же относительно оси, проходящей через средние грани, добиться не удастся, сколько бы Вы не пытались.
При наличии же внешнего воздействия, например, со стороны нити, за которую подвешено вращающееся тело, устойчивым оказывается только вращение вокруг главной оси, соответствующей наибольшему значению момента инерции. Именно по этой причине тонкий стержень, подвешенный на нити, прикрепленной к его концу, при быстром вращении будет вращаться вокруг перпендикулярной к нему оси, проходящей через центр (рис.5).
Рис. 5

![]()
где
![]() проекции вектора угловой скорости на
главные оси инерции.
проекции вектора угловой скорости на
главные оси инерции.
Следует отметить еще одно важное свойство. Каждый из трех главных моментов инерции не может быть больше суммы двух других:
![]()
![]()
![]()
Определим моменты инерции осесимметричного тела – прямоугольного параллелепипеда относительно главных осей инерции (рис.6).
Рис. 6
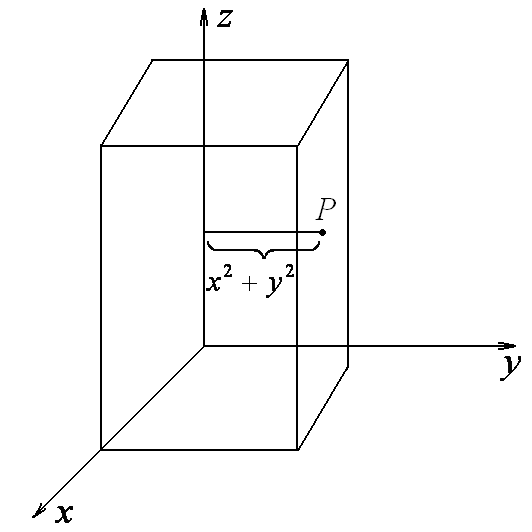
![]()
где
![]() плотность
материала параллелепипеда; V
– его объем,
плотность
материала параллелепипеда; V
– его объем,
![]()
![]()
тогда
![]()
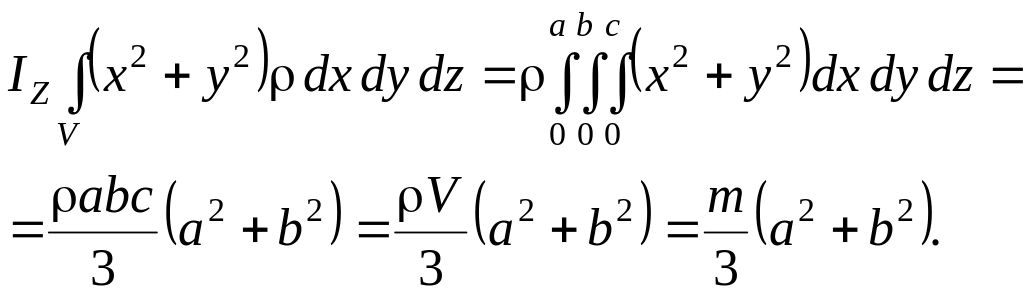 (1)
(1)
Аналогично:
![]() (2)
(2)
![]() (3)
(3)
Ось инерции,
проходящую через диагональ параллелепипеда,
называют его главной осью. Момент инерции
относительно этой оси обозначим
![]() ,
т.к. главные оси инерции являются осями
симметрии, можно сказать, что
,
т.к. главные оси инерции являются осями
симметрии, можно сказать, что
![]() (4)
(4)
