
- •7. Вычислить выражения:
- •1. Вычислить:
- •Задание № 4-2.
- •3. Вычислить определители:
- •Задание 6-1.
- •Задание № 7-1.
- •Задание № 8-5.
- •Задание 9-3.
- •2.Вычислить выражения:
- •Ответы.
- •Задание 102.
- •Ответы.
- •Задание № 13 4.
- •Ответы.
- •Задание № 142.
- •Ответы.
- •Задание № 155.
- •Ответы .
- •Задание № 16-4.
- •Ответы.
- •Задание № 17-2.
- •Задание № 22-2.
- •Ответы.
- •Задание № 23 3.
- •Ответы.
- •Задание 244.
- •Ответы.
- •25. Задания для самостоятельной работы.
- •Ответы.
- •26. Задачи и упражнения для самостоятельной работы
- •Ответы.
- •Задание № 275.
- •28. Задачи для самостоятельного решения
- •5. Написать уравнение плоскости, инвариантной относительно линейного преобразования , заданного в некотором ортонормированном базисе матрицей
- •9. Ответы к задачам для самостоятельного решения
- •29. Задачи для самостоятельного решения
- •Ответы к задачам для самостоятельного решения
- •30. Задачи для самостоятельного решения.
- •Ответы к задачам для самостоятельного решения.
3. Вычислить определители:
![]()
![]()
4. Предложить схему вычисления определителей 3-го порядка,
отличающуюся от “правила “треугольников”.
5. Предложить схему вычисления определителей 4-го порядка.
Ответы
1а.
Умн. на
![]() .
2. Тождество. 3д. (af
be + cd)2.
.
2. Тождество. 3д. (af
be + cd)2.
3а. 17. 3е. (x x1)(x x2)...(x xn).
1б. Не изменится. 3б. 6. . 3ж. (a0 + a1 +...+ an)xn.
1в. 0 или произв. 3в. 150.
этих элем. 3г. 52.
Задание 6-1.
1. Вычислить определители приведением к треугольному виду:
![]()
2. Вычислить определители методом рекуррентных соотношений.
![]()
3. Вычислить определители методом представления их в виде суммы
определителей или другим методом.
![]()
![]()
Ответы
n!.
2.
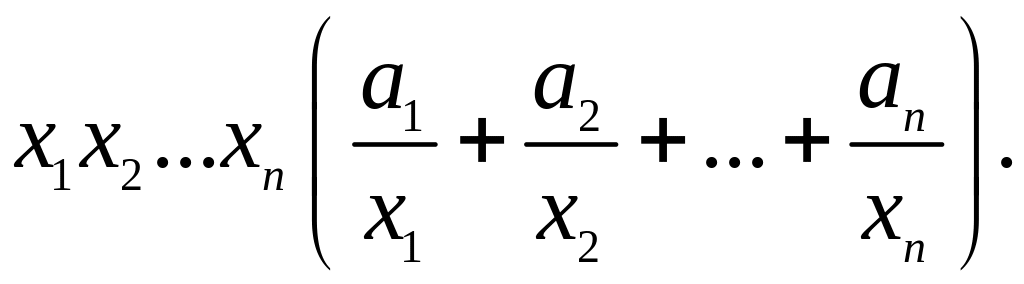
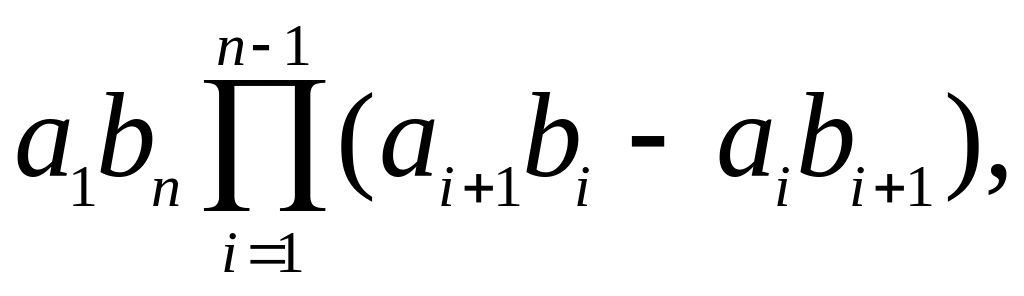 Указание:
получить соотношение:
Указание:
получить соотношение:
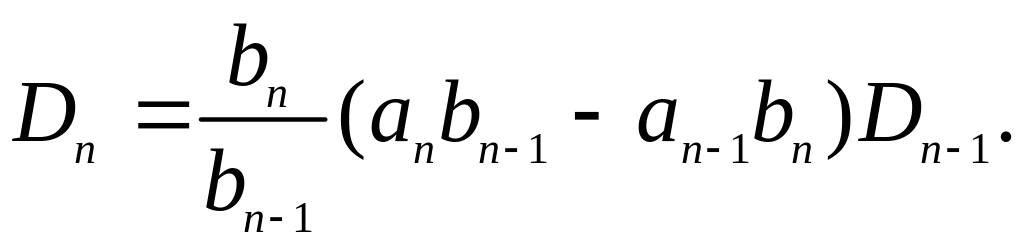
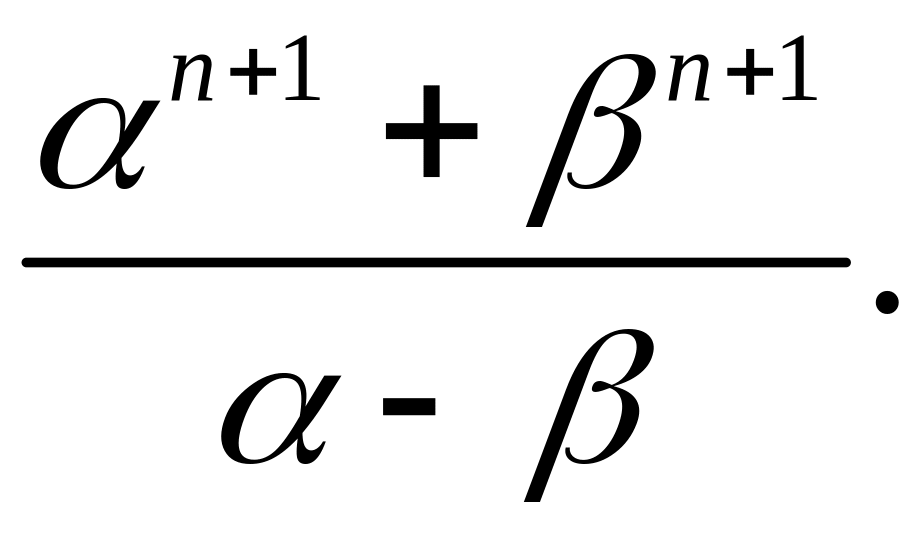
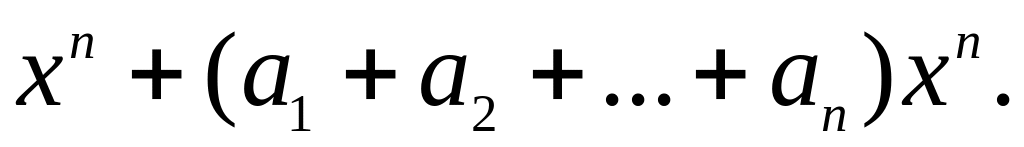 Указание:
Элементы вне главной диагонали
представить:
Указание:
Элементы вне главной диагонали
представить:

(n 1)!.
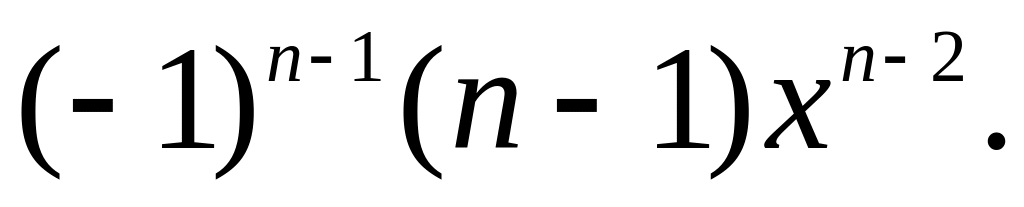
8. (x x1)(x x2)...(x xn).
Задание № 7-1.
1.Найти вектор х из уравнения
а1 + 2а2 + 3а3 + 4х = 0, где а1 = (5, 8, 1, 2), а2 = (2, 1, 4, 3),
а3 = (3, 2, 5, 4).
2.Выяснить, являются ли следующие системы векторов линейно независимыми: а) а1 = (1, 0, 0, 2, 5), а2 = (0, 1, 0, 3, 4), а3 = (0, 0, 1, 4, 7),
а4 = (2, 3, 4, 11, 12);
б) а1 = (4, 5, 2, 6), а2 = (2, 2, 1, 3), а3 = (6, 3, 3, 9), а4 = (4, 1, 5, 6).
3.Система векторов а1, а2,...аk линейно независима. Выяснить, являются ли линейно зависимыми системы векторов:
а) b1 = 3а1 + 2а2 + а3 + а4, б) b1 = а1 а2,
b2 = 2а1 + 5а2 + 3а3 + 2а4, b2 = а2 а3,
b3 = 3а1 + 4а2 + 2а3 + 3а4. ……………
bk1 = аk-1 аk,
bk =аk а1.
4.Найти все значения , при которых вектор b линейно выражается через векторы a1, а2,...,аk: а1 = (2, 3, 5), а2 = (3, 7, 8),
а3 = (1, 6, 2), b = (7, 2, ).
5.Найти какой ни будь базис системы векторов и выразить через него остальные векторы системы:
а) а1 = (5, 2, 3, 1), а2 = (4, 1, 2, 3), а3 = (1, 1, 1, 2), а4 = (3, 4, 1, 2),
а5 = (7, 6, 7, 0);
б) а1 = (2, 1, 3, 5), а2 = (4, 3, 1, 3), а3 = (3, 2, 3, 4), а4 = (4, 1, 15, 17).
Ответы
1. (0, 1, 2, 2). 3б. Да.(л. зав.)
2a. Да.(л. нез.) 4. = 15.
2б. Нет. (л. зав.) 5а. (a1, a2, a4), a3 = a1 a2.
3а. Нет.(л. нез.) 5б. (a1, a2, a3), a4 = 2a1 3a2 + 4a3, a5 = a1 + 5a2 5a3 .
Задание № 8-5.
1.Найти ранг матриц с помощью элементарных преобразований:
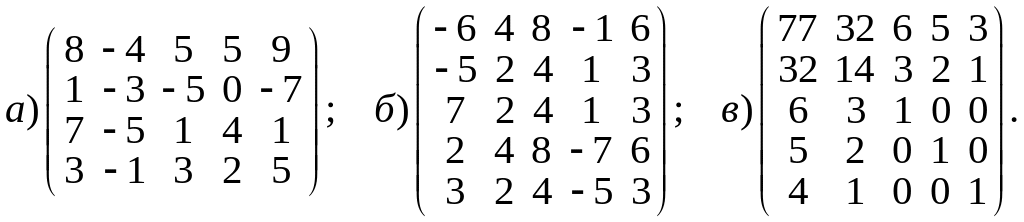
2.Вычислить ранг следующих матриц:
а) 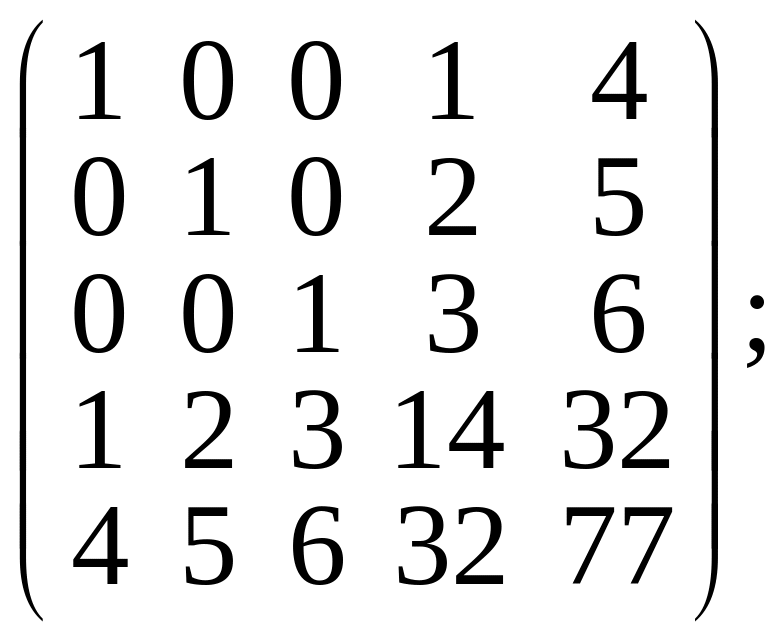 б)
б)
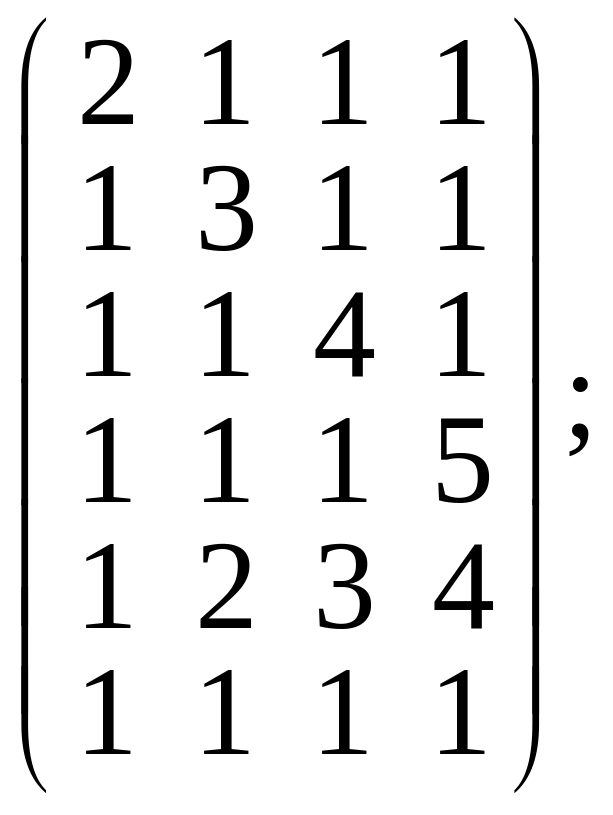 в)
в)
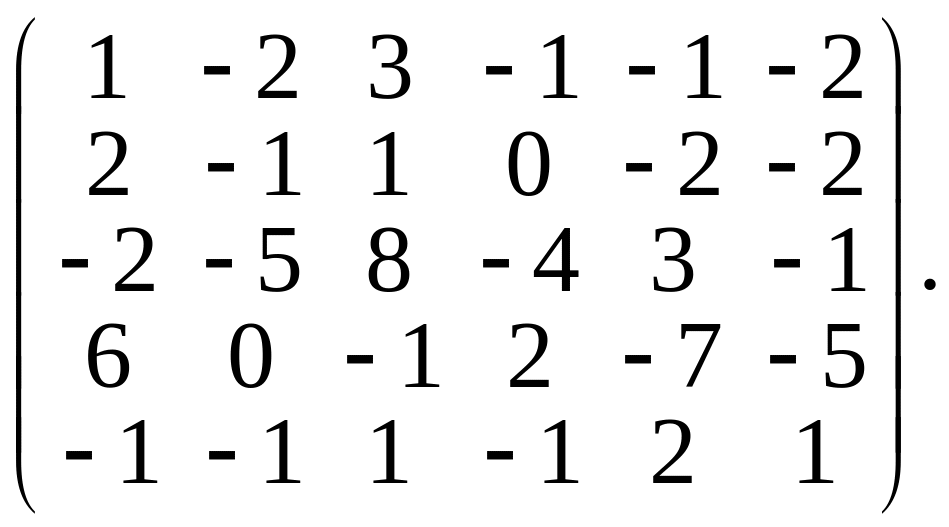
3.Найти ранг матрицы при различных значениях параметра :
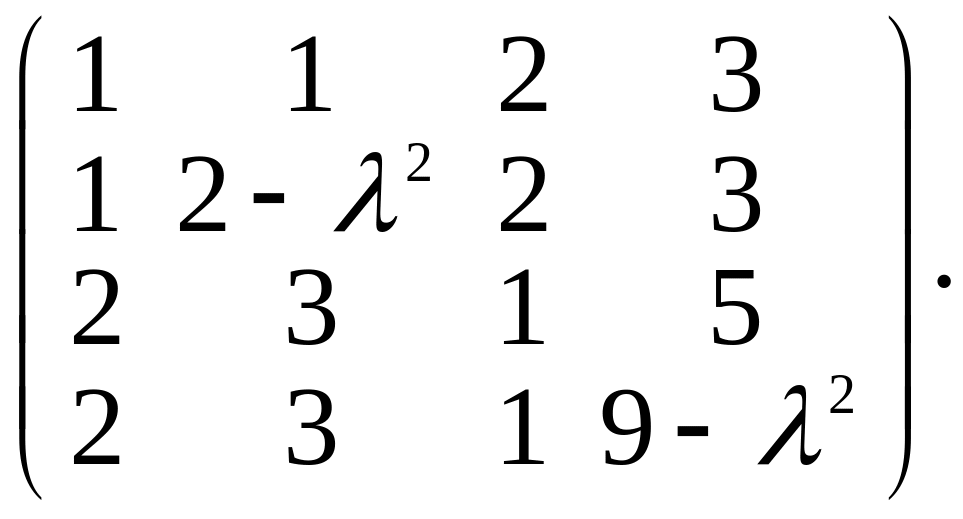
4.Пусть А - (mxn)-матрица и В - (mx(n+k))-матрица, получающаяся из матрицы А приписыванием k новых столбцов. Докажите, что:
а)Если строки матрицы В линейно зависимы, то и строки матрицы А линейно зависимы.
б)Ранг матрицы А не превосходит ранга матрицы В.
Ответы
1а. 3. 1б. 3. 1в. 4.
2а. 3. 3. 3 при = 1, при = 2.
2б. 4.
2в. 3. 4. Док-во.
