
- •7. Вычислить выражения:
- •1. Вычислить:
- •Задание № 4-2.
- •3. Вычислить определители:
- •Задание 6-1.
- •Задание № 7-1.
- •Задание № 8-5.
- •Задание 9-3.
- •2.Вычислить выражения:
- •Ответы.
- •Задание 102.
- •Ответы.
- •Задание № 13 4.
- •Ответы.
- •Задание № 142.
- •Ответы.
- •Задание № 155.
- •Ответы .
- •Задание № 16-4.
- •Ответы.
- •Задание № 17-2.
- •Задание № 22-2.
- •Ответы.
- •Задание № 23 3.
- •Ответы.
- •Задание 244.
- •Ответы.
- •25. Задания для самостоятельной работы.
- •Ответы.
- •26. Задачи и упражнения для самостоятельной работы
- •Ответы.
- •Задание № 275.
- •28. Задачи для самостоятельного решения
- •5. Написать уравнение плоскости, инвариантной относительно линейного преобразования , заданного в некотором ортонормированном базисе матрицей
- •9. Ответы к задачам для самостоятельного решения
- •29. Задачи для самостоятельного решения
- •Ответы к задачам для самостоятельного решения
- •30. Задачи для самостоятельного решения.
- •Ответы к задачам для самостоятельного решения.
Задание № 1-3.
Вычислить выражения:

Вычислить i98.
Решить систему:

4.
Доказать, что комплексное число z
является чисто мнимым тогда и только
тогда, когда
![]() =
z.
=
z.
5. Найти комплексные числа, сопряженные к своему кубу.
6. Найти тригонометрическую форму чисел:
![]()
7. Вычислить выражения:
8.
Вычислить:

Ответы
1а.
![]() ,
1b.
52i.
2. 1.
3. z1=1i,
z2=
,
1b.
52i.
2. 1.
3. z1=1i,
z2=![]() 4. Док-во. 5.
4. Док-во. 5.![]()
6.


Задание № 2-1.
1. Вычислить:

2. Определить сумму первообразных корней из 1: а) 6-ой степени;
б) 15-ой степени.
3. Вычислить все корни 2-ой и 24-ой степеней из 1 и указать первообразные.
4.
Решить уравнение:
![]()
Ответы.
1а.
i,
 .
2a. 1.
.
2a. 1.
1б.
![]() 2б. 1.
2б. 1.
1в. 64. 3. №№ 1, 5, 7, 13, 17, 19, 23.
1г.
![]() 4. z
=
3
+
4i.
4. z
=
3
+
4i.
Задание № 3-4.
Решить методом Гаусса системы уравнений:
а)
 б)
б)

в)
 г)
г)

д)
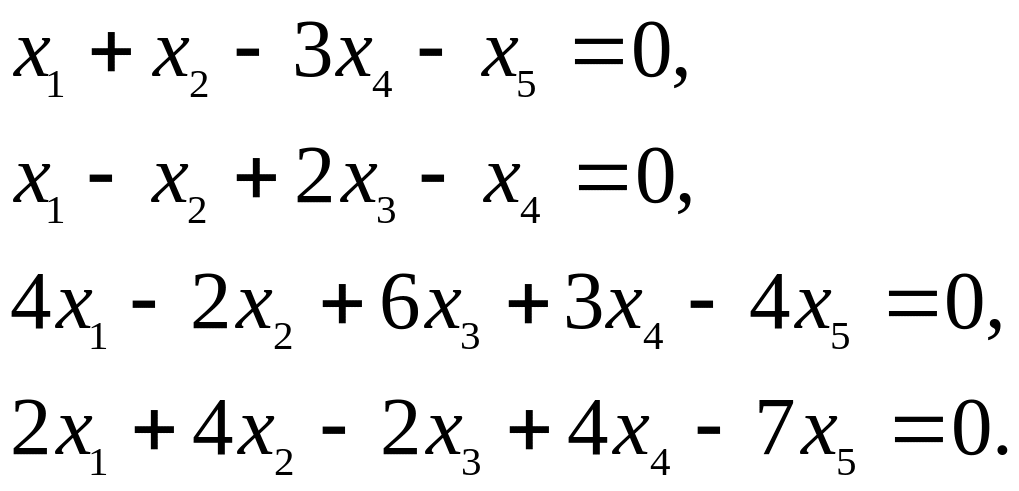 е)
е)

Исследовать системы и найти общее решение в зависимости от значений параметров:
а)
 б)
б)

в)
 г)
г)

Ответы.
1а. x1 = 1/2, x2 = 2/3, x3 = 2, x4 = 3. 1г. x1 =1, x2 = 2, x3 = 1.
1б. x1 = 1/10(6 15x2 x4 ), 1д. х1 = 7/6x5 x3 , x2 = 5/6x5 + x3,
x3 = 1/5(1 + 4x4). х4 = 1/3x5.
1в. x1 = x2 =0, x3 = x4. 1e. x1 = 16+x3 + x4 + 5x5,
x2 = 23 2x3 2x4 6x5.
2a. = 8: x3 = 1, x4 = 2 x1 3/2x2, 8: x2 = 4 2/3x1, x3 = 1, x4 = 0.
2б. 1, 2: x1 = x2 = x3 = 1/ +2, = 1: x1 = 1 x2 x3 ,
= 2: решений нет.
2в.
При
= 0, ![]() реш. зависит от одного параметра. В
других слу-
реш. зависит от одного параметра. В
других слу-
чаях только нулевое решение.
2г.
![]()
 ,
= 1: реш. зависит от 3-х парам.,
= 3:
решений нет.
,
= 1: реш. зависит от 3-х парам.,
= 3:
решений нет.
Задание № 4-2.
1. Вычислить определители:
![]() ;
;
![]()
2.
Пользуясь теоремой Крамера, решить
системы:![]()
![]()
3. Перемножить перестановки в указанном и обратном порядке.
![]()
4.
Найти обратную перестановку:
![]() .
.
5. Определить число инверсий в последовательностях:
а) 2, 3, 5, 4, 1; б) 6, 3, 1, 2, 5, 4; в) 1, 3, 5, 7, ... , 2n-1, 2, 4, 6, 8, ... , 2n.
6. Определить четность перестановок:
![]()
7. С какими знаками входят данные произведения в определители соответствующих порядков ?
![]()
8.
Выписать все слагаемые, входящие в
состав определителя 4-го порядка со
знаком ””
и содержащие множитель
![]() .
.
9. С каким знаком входит в определитель порядка n произведение элементов побочной диагонали ?
Ответы
1а.
a2 +
b2 +
c2 +
d2.
1б.
1.
1в.
1. 1г.
100. 1д.
0. 1е.
3i![]() .
2a. х1 =
3, x
.
2a. х1 =
3, x![]() =
1.
2б.
x = a,
y = b, z = c. 2в.
x1 =
3, x2 =
x = x3 =
1.
=
1.
2б.
x = a,
y = b, z = c. 2в.
x1 =
3, x2 =
x = x3 =
1.
3а.
![]() 3б.
3б.
![]() 3в.
3в.
![]()
4а.
![]() 4б.
4б.
![]() 5а.
5. 5б.
8. 5в.
5а.
5. 5б.
8. 5в.
![]() 6а.
3().
6б.
11().
6в.
неч.
7а.
().
7б.
(+). 7в.
(+).
6а.
3().
6б.
11().
6в.
неч.
7а.
().
7б.
(+). 7в.
(+).
8.
a11 a23 a32 a44,
a12 a23 a34 a41,
а14
a23 a31 a42.
9.
![]()
Задание 5-5.
1. Как изменится определитель порядка n, если:
а) его столбцы записать в обратном порядке ?
б) каждый его элемент заменить на симметричный относительно “центра”
определителя ?
в) Чему может быть равен определитель порядка n, в котором только n элементов
отличны от нуля ?
2. Пользуясь свойствами определителей, доказать тождество:
![]()
