
- •Оглавление
- •2. Таблица значений функции 44
- •3. Таблица значений функции 45
- •Предисловие.
- •Введение (справочный материал к контрольным заданиям).
- •Геометрическое определение вероятности.
- •Контрольная работа №1.
- •Контрольная работа №2.
- •Контрольная работа №3.
- •Решения задач нулевых вариантов. Контрольная работа №1.
- •Контрольная работа №2.
- •Контрольная работа №3.
Контрольная работа №2.
Задача №7. Контрольный тест содержит 10 вопросов, каждый из которых требует выбор правильного ответа из четырех данных, один из которых, правильный, а остальные неправильные. Найти наиболее вероятное число правильных ответов, которое даст тестируемый, знающий 3 вопроса. Найти вероятность того, что тестируемый даст наиболее вероятное число правильных ответов.
Решение.
Пусть
- наиболее вероятное число правильных
ответов, которое даст тестируемый,
отвечая наудачу на 7 вопросов теста,
которых он не знает. Тогда общее число
наиболее вероятного числа правильных
ответов будет
![]() .
Итак, найдем
:
.
Итак, найдем
:
![]() -
целое, следовательно,
-
целое, следовательно,
![]() или
или
![]() .
Поэтому
.
Поэтому
![]() или
или
![]() .
Это означает, что
.
Это означает, что
![]() и искомая вероятность равна:
и искомая вероятность равна:
![]() .
.
Ответ:
4 или 5;
![]() .
.
Задача №8. Стрелок производит 4 выстрела по движущейся мишени. Вероятность попадания при первом выстреле 0,4; при втором – 0,3; при третьем – 0,2; при четвертом – 0,1. Найти вероятности следующих событий:
А – стрелок попадет в мишень 2 раза;
В – стрелок попадет в мишень хотя бы 1 раз;
С – стрелок ни разу не попадет в мишень.
Решение.
Вероятность промаха при первом выстреле 0,6; при втором – 0,7; при третьем – 0,8 и при четвертом выстреле 0,9.
Составим производящую функцию (многочлен)
![]() .
.
Если
раскроим скобки, сделаем приведение
подобных членов и запишем многочлен по
возрастающим степеням, то вероятность
![]() попаданий будет равна коэффициенту при
попаданий будет равна коэффициенту при
![]() .
Итак:
.
Итак:

![]()
![]() .
.
Ответ:
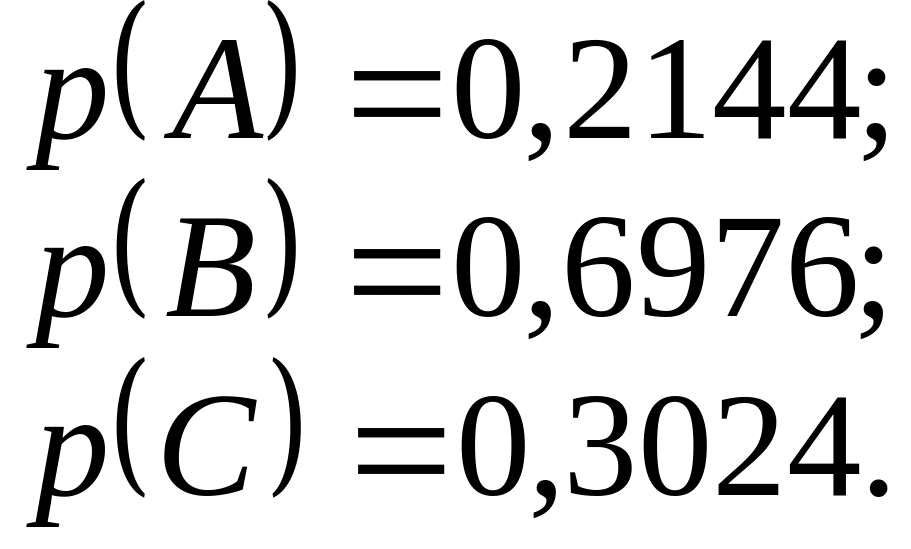
Задача №9. Игральная кость подбрасывается 4 раза. Найти вероятность того, что: 1 очко выпадает 2 раза, 2 очка – 1 раз и 3 очка – 1 раз.
Решение.
По полиномиальной формуле, обобщающей формулу Бернулли, имеем:
![]() .
.
Ответ:
![]() .
.
Задача №10. 100 станков работают независимо друг от друга, причем вероятность бесперебойной работы каждого станка в течение смены равна 0,8. Найти вероятность того, что в течение смены бесперебойно проработают:
82 станка;
От 80 до 85 станков.
Решение.
Так
как
![]() ,
то в пункте:
,
то в пункте:
применим локальную приближенную формулу Муавра-Лапласа и в пункте
интегральную приближенную формулу Муавра-Лапласа.
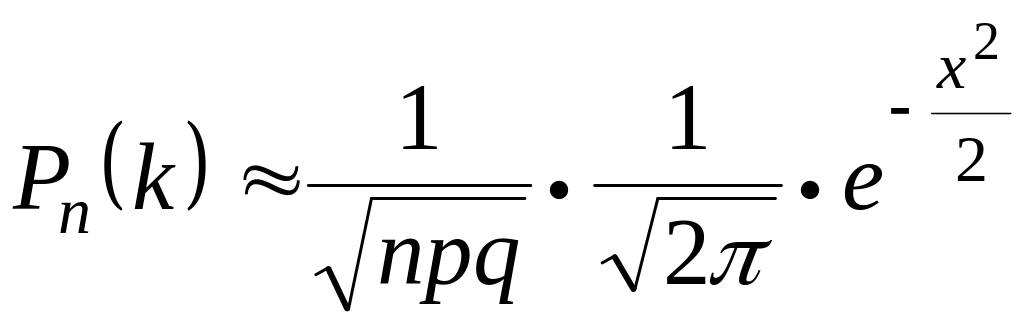 ,
где
,
где
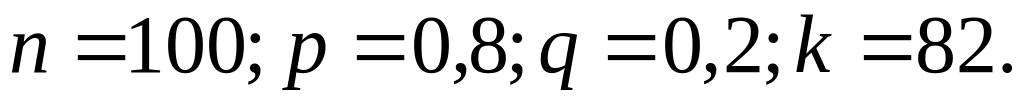
Итак:
![]() ,
где
,
где
![]() .
.
Находим:
![]()
![]() -
найдено по таблице для
-
найдено по таблице для
![]() (Приложение 1).
(Приложение 1).
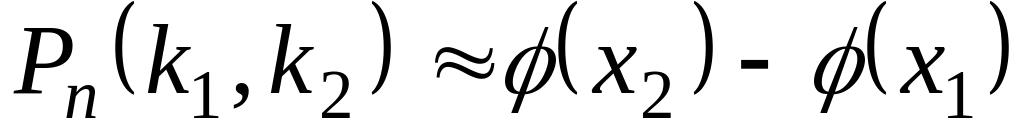 ,
где
,
где
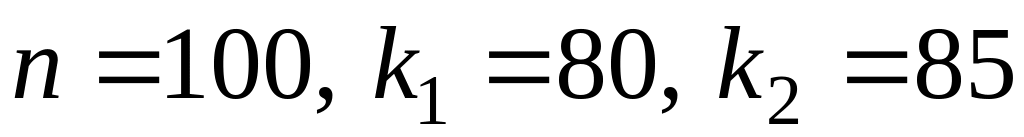 .
Находим
.
Находим
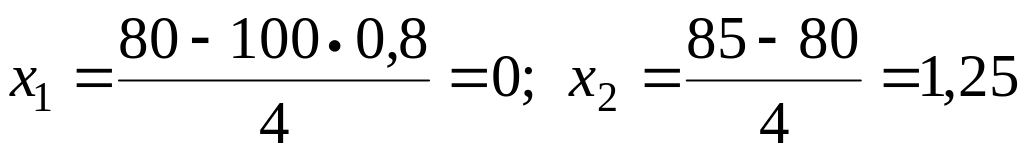 .
.
Значения
![]() находим по таблице для функции Лапласа
находим по таблице для функции Лапласа
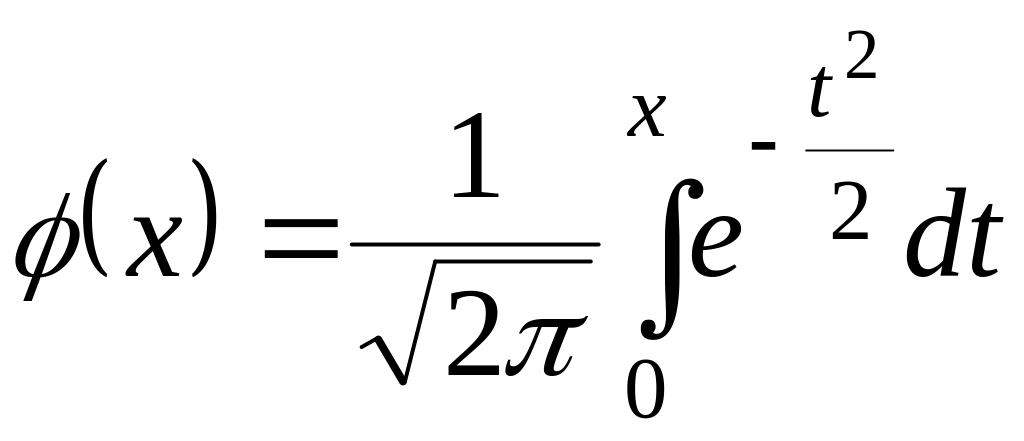 (Приложение
2).
(Приложение
2).
Итак:
![]() и получаем
и получаем
![]() .
.
Ответ:
а)
![]()
б)
![]() .
.
Задача №11. На торговую базу завод отправил 1000 бутылок минеральной воды. Вероятность повреждения при транспортировке для каждой бутылки равна 0,002. Найти вероятность повреждения:
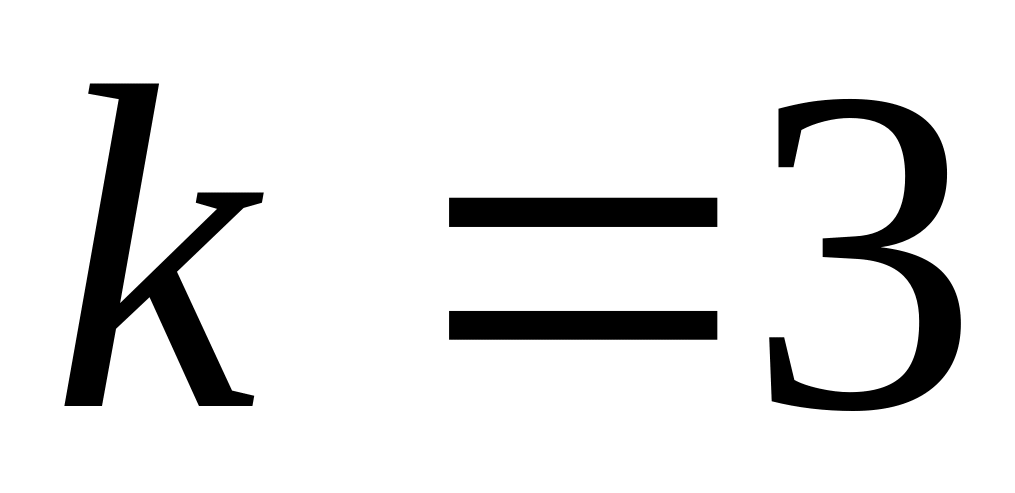 ;
;
от
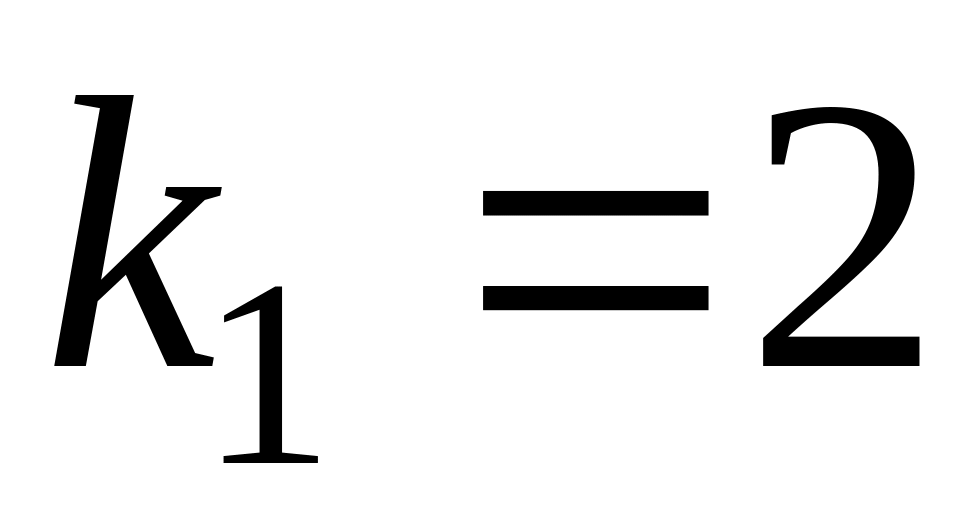 до
до
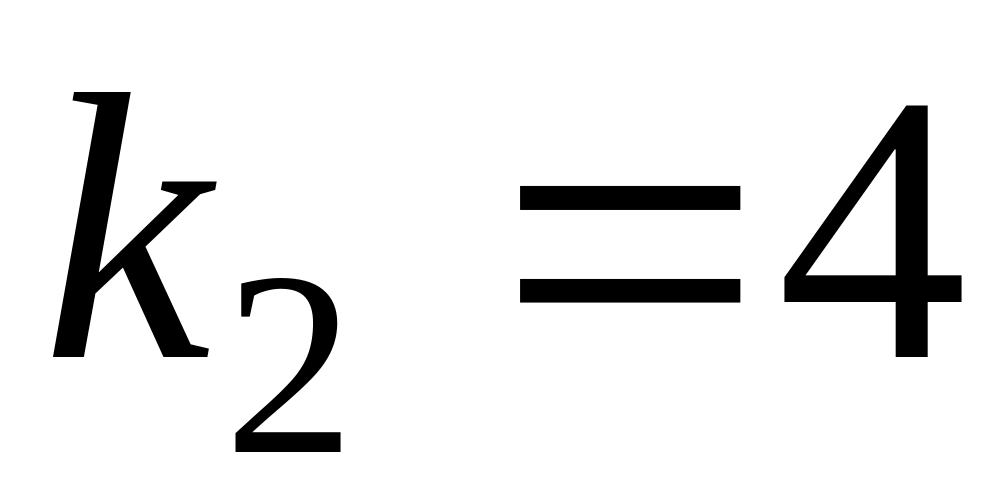 ;
;более 3-х бутылок.
Решение.
![]() ,
поэтому воспользуемся формулой Пуассона
для редких событий:
,
поэтому воспользуемся формулой Пуассона
для редких событий:
![]() ,
где
,
где
![]() .
.
а)
.
Находим
![]() по таблице для функции
по таблице для функции
![]() при
при
![]() .
Находим
.
Находим
![]() .
.
б)
![]() .
.
в)
![]() .
.
Ответ: а) 0,18045;
б) 0,54134;
в) 0,14289.
Задача
№12.
Найти закон распределения случайной
величины
- числа изделий высшего сорта среди 5
наудачу извлеченных из коробки изделий,
если в коробке 8 изделий, среди которых
3 изделия высшего сорта. Найти
![]() .
.
Решение.
Ясно, что может принимать значения 0,1,2,3 с вероятностями:
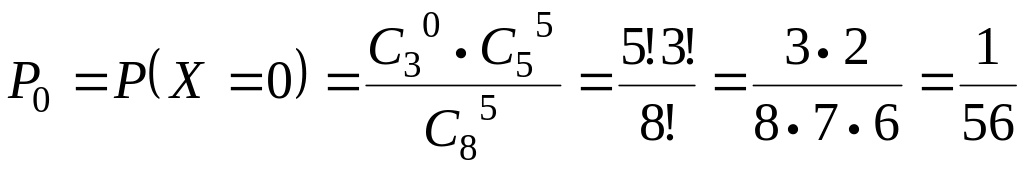
![]() ;
;
![]() ;
;
![]() .
.
Закон распределения :
-
0
1
2
3
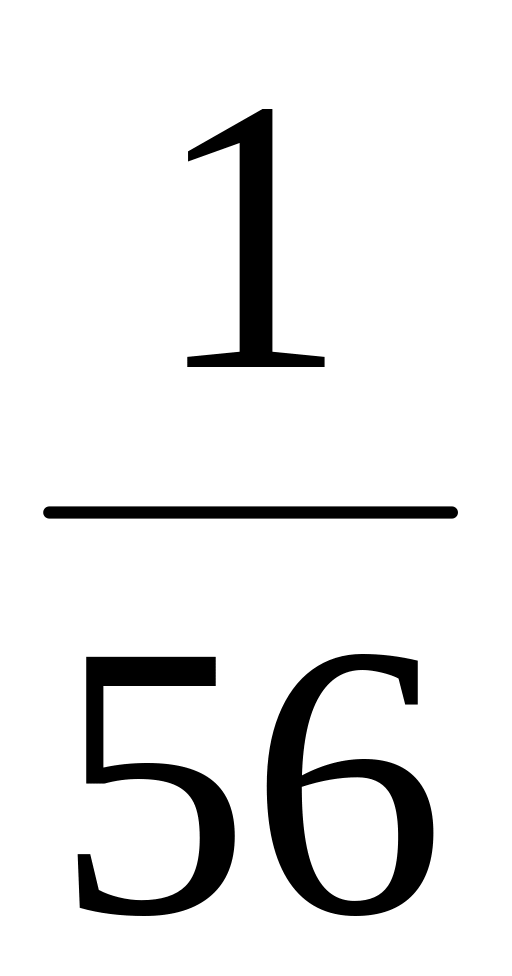
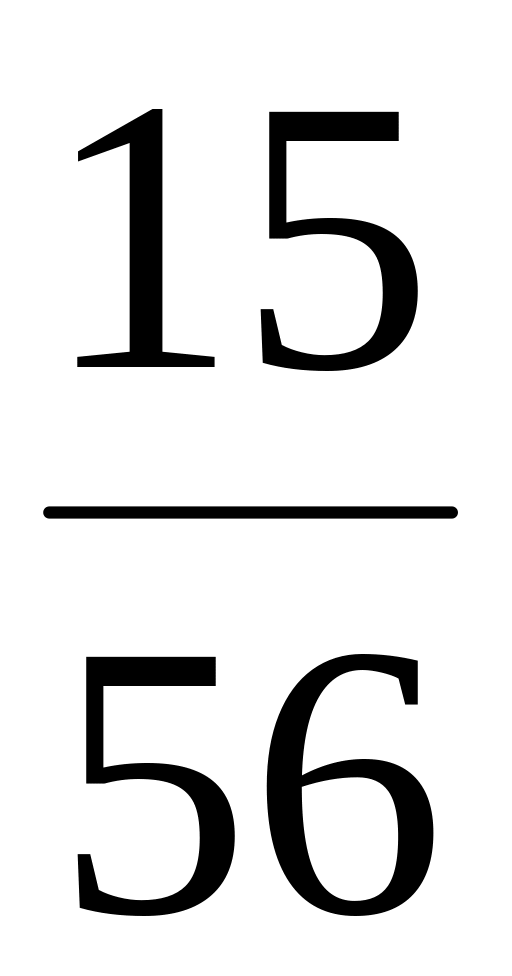
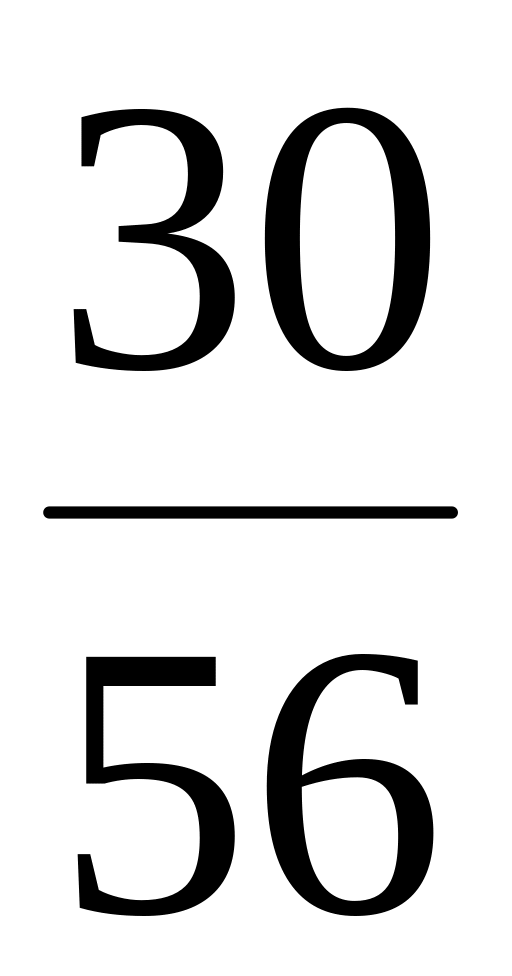
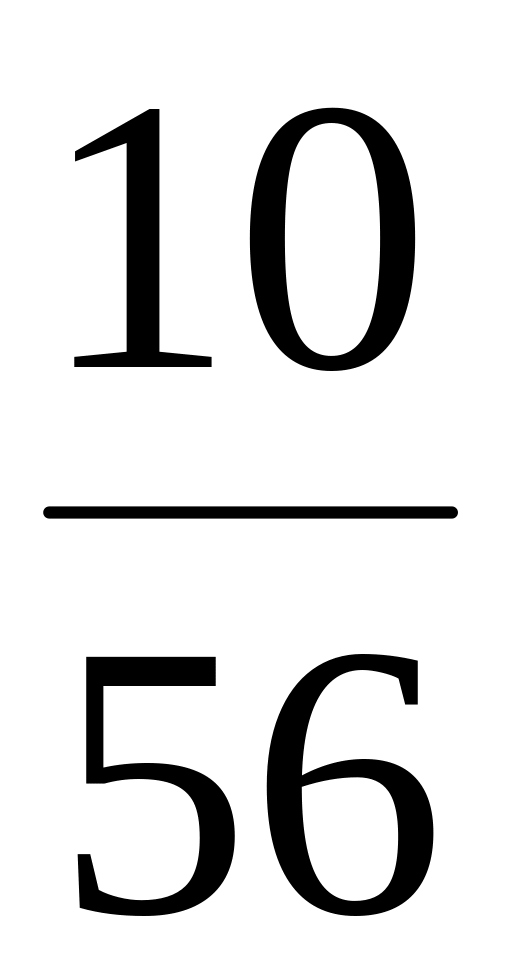
![]() .
.
![]()
![]() ;
;
![]() .
.
Ответ:
![]() .
.
Задача
№13.
Мишень разделена на три зоны: I,
II,
III.
За попадание в зону I
дается 1 очко, за попадание в зону II
– 2 очка и за попадание в зону III
– 3 очка. Вероятности попадания в зоны
I,
II,
III
соответственно равны
![]() .
Найти закон распределения случайной
величины
,
равной числу заработанных очков стрелком
при двух независимых выстрелах по
мишени. Найти
.
.
Найти закон распределения случайной
величины
,
равной числу заработанных очков стрелком
при двух независимых выстрелах по
мишени. Найти
.
Решение.
Пусть
![]() - число очков, заработанных стрелком
при первом выстреле;
- число очков, заработанных стрелком
при первом выстреле;
![]() - при втором выстреле.
Тогда
- при втором выстреле.
Тогда
![]() ,
так как
,
так как
![]() независимы.
независимы.
Законы
распределения
![]() задаются таблицами:
задаются таблицами:
-
1
2
3
1
2
3

0,3
0,2
0,5
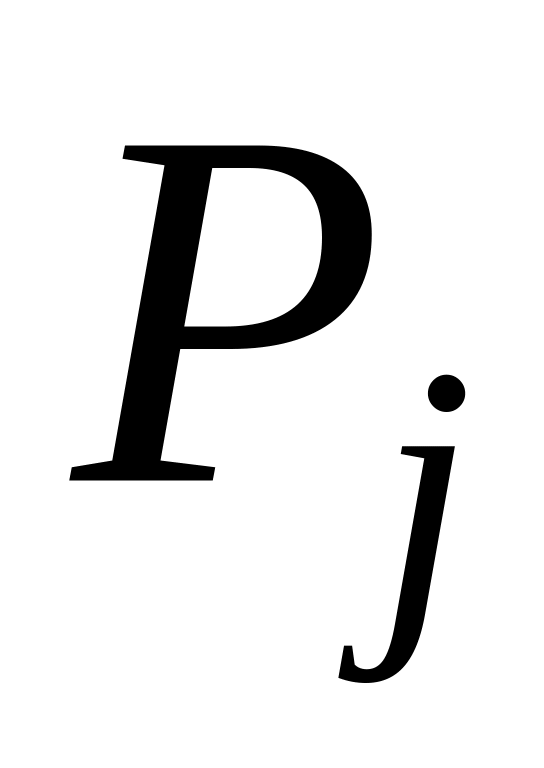
0,3
0,2
0,5
Имеем:
|
: |
2 |
3 |
4 |
3 |
4 |
5 |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
4 |
5 |
6 |
|
|
|
|
: |
|
|
|
|
|
|
Закон
распределения
![]() :
:
-
2
3
4
5
6
0,09
0,12
0,34
0,2
0,25
![]()
![]()
![]() .
.
Ответ:
![]() .
.
Вычисления можно было произвести, исходя из закона распределения .
