- •10) Понятие прямой теоремы и произвольных от неё высказываний
- •11) Т. О проекции:
- •1)Таблица для коньюкции
- •6) Терм
- •10) Т.О полноте
- •1)Дизъюнкция
- •3) Лемма о немонотонной ф-ии
- •6) . Основная т. О рекурсивно перечислимых мн-вах:
- •7) Проблемма остановки
- •8) Оператор примитивной рекурсии
- •9)Изоморфизм моделей
- •2) О существование скнф
- •3) Лемма о немонотонной ф-ии
- •6) Оператор минимизации
- •7) Понятие теории, полные разрешимые , категоричные теории
- •9) Т. Поста (критерий рекурсивности мн-ва).
- •10) . Тезис Чёрча.
- •Штрих шеффера
- •2) Теоремы о нормальных формах
- •8) Машина Тьюринга
- •10) Эрбранова область
- •1. Если в формуле есть константный символ с, то ;
- •2) Формулы ив:
- •3) Класс монотонных функций
- •4) Опр.Класс предполный
- •6)Т. Компактности.
- •10) Теорема о теории модели
- •4) Лемма о нелинейной ф-ии:
- •5) Определение формулы в лп
- •8) Тезис Чёрча.
- •8)Вариант
- •2) . Рекурсивно перечислимымые множества
- •3) Аксиомы ив Генцена.
- •4) . Т. О графике:
- •1) Ч.Р. Фун рек. Пер. Множ.
- •5) Т Поста. О полноте системы булевых ф-ий.
- •6)Т. Компактности.
- •7) Полином Жигалкина
- •8)Ответ
- •9 Вариант
- •3) ) Лемма о немонотонной ф-ии
- •4) Понятие прямой теоремы и произвольных от неё высказываний
- •5)Правило вывода Ив генсена
- •7) Т.(о полноте ив Гильбрта)
- •9) Т. Поста (критерий рекурсивности мн-ва).
- •1)Дизъюнкция
- •2) Фиктивные и существенные переменные.
- •3) Теоремма о разложении булл функции
- •4) Понятие прямой теоремы и произвольных от неё высказываний
- •6)Т о дедукции
- •8)Вывод генсена
- •9) Т. О проекции:
- •3) Теорема о существовании единственной сднф
- •9) Основная т. О рекурсивно перечислимых мн-вах:
- •10) Т. О проекции:
- •2)Кнф и скнф
- •5) Т. О неподвижной точке:
- •Предложение
- •1) Ч.Р. Фун рек. Пер. Множ.
- •Все эквивалентности лв.
- •Если фор-ла , не содержит связную переменную у : ;
- •Если не содержит переменных y,z ; X-свобод
- •9)Наитии Эрбран область
- •10) Два класса префиксов:
- •14Вариант
- •3) Теоремма о разложении булл функции
- •7)Вычисл функции
- •8) Оператор суперпозиции:
- •1) Булевые ф-ции одной переменной
- •2) Принцип двойственности
- •7) Понятие теории, полные разрешимые , категоричные теории
- •8) Оператор примитивной рекурсии
- •9) Т. О неподвижной точке:
- •10) Эрбранова область
- •1. Если в формуле есть константный символ с, то ;
- •2) Т. О замене
- •3) Понятие прямой теоремы и произвольных от неё высказываний
- •5) Не противоречивость множ-ва формул и выводимости
- •6) Два класса префиксов:
- •8) Вычислимость функции на мт
- •5) Т. О дедукции:
- •7) Понятие теории, полные разрешимые , категоричные теории
- •8) Вычислимость функции на мт
- •9) Т. Поста (критерий рекурсивности мн-ва).
- •19 Вариант
- •3) Теоремма о разложении булл функции
- •20 Вариант
- •2) Т. О дедукции.
- •5) Тезис Чёрча.
- •6) Т. О неподвижной точке:
- •7) Оператор суперпозиции:
- •8) Т. Компактности.
9) Т. Поста (критерий рекурсивности мн-ва).
Мн-во
А – рекурсивное
А и
 (дополнение к А) – рекурсивно перечислимы.
(дополнение к А) – рекурсивно перечислимы.
10) . Тезис Чёрча.
Класс интуитивно вычислимых ф-ий совпадает с классом ф-ий вычислимых по Тьюрингу.
11) Ф-лы ЛВ:
Атомарная
ф-ла:
 .
.
Опр.Формулой
наз.: а) всякая атомарная ф-ла; б) если
слова
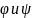 явл. ф-ми
явл. ф-ми
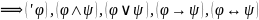 - ф-лы
- ф-лы
5 вариант=25вариант=45вариант(наверно)
Штрих шеффера
x |
y |
x|y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
2) Теоремы о нормальных формах
О существование СДНФ
Пусть f
при этом f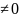 .
Тогда существует СДНФ от
представляющая f
причем единственная с точностью до
порядка конъюнктов и литер в этих
конъюнктах
.
Тогда существует СДНФ от
представляющая f
причем единственная с точностью до
порядка конъюнктов и литер в этих
конъюнктах
О существование СKНФ
Пусть f при этом f . Тогда существует СKНФ от представляющая f причем единственная с точностью до порядка дизъюнктов и литер в них
3) Т Поста. о полноте системы булевых ф-ий.
Система
булевых ф-ий

 не содержится полностью ни в одном из
классов
не содержится полностью ни в одном из
классов
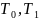 ,
,
 ,
L
,
L
4)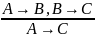 - правило силлагизма(закон цепных
рассуждений);
- правило силлагизма(закон цепных
рассуждений);
5) Непротиворечивость и выводимость:
Опр.
Выводимость: ф-ла
выводится из множества фор-л Г:Г
вывод
вывод
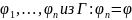 .Последов
.Последов
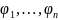 называется выводом из множ Г, если кажд.
называется выводом из множ Г, если кажд.
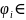 Г
(гипот),либо аксиома, либо
Г
(гипот),либо аксиома, либо
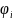 получ МР из формул
получ МР из формул
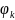 ,
,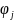 ;
j<k<i;
;
j<k<i;
Опр. Множество формул Г называется противоречивым, если сущ.формула φ:Г⊢φ и Г⊢ (φ.) ̅ Если такой не сущ , то Г не противореч.
6) Модели и интерпритация формул данной сигнатуры.
Опр.
Структура А(греческая с расслоённым
концом) с сигнатурой
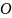 интерпритация
называется моделью предложения
,
если при данной интерпритации предложение
интерпритация
называется моделью предложения
,
если при данной интерпритации предложение
 А
истинно А
А
истинно А
7) Т. о полноте.
Теорема. Геделя(о полноте)
Множество формул не противоречиво Г имеет модель.
⊢φ⟺⊨φ(теорема тогда и только тогда, когда тавтология)
Теорема Геделя (обобщенная теорема о полноте)
Г -предложение
Г
-предложение
Г
Логика высказывания и ИВ Гильберта:
Т.(о полноте ИВ Гильбрта)
Т.( обобщен теорема о полноте)

Т. компактности. Мн-во формул Г – выполнимо каждое конечное подмн-во Г выполнимо
Т.
об адекватности логики ИВ Гильберта и
ЛВ. Пусть Г – мн-во формул, -формула.
Тогда следующие утверждения верны: 1.
 (Т о
модели); 2.)
(Т о
модели); 2.)
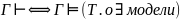 ;
3)
(обобщенная Т. о полноте ИВ Гильберта);
4)
;
3)
(обобщенная Т. о полноте ИВ Гильберта);
4)
 (Т. о полноте)
(Т. о полноте)
8) Машина Тьюринга
состоит из след элементов:
1)два конечных мн-ва
A={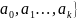 -
внешний алфавит
-
внешний алфавит
Q={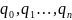 }-
внутренний алфавит
}-
внутренний алфавит
2)лента разбитая на ячейки, потенциально бесконечная (в кажд момент времени врем конечно можем дополнить сколь угодно в разные стороны). Каждая ячейка содержит один символ внешнего алфавита.
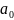 -
символ пустой ячейки.
-
символ пустой ячейки.
3) Управляющее устройство (каретка)-В каждый момент времени работает с одной ячейкой. Коретка может прочитать/записать символ в ячейку и переместиться в соседн ячейку.
4) В каждый момент времени машина нах во внутр состоянии И каждое внутреннее состояние об-ся символом алфавита Q.
 начальное
состояние
начальное
состояние
 конечное
состояние
конечное
состояние
5) программа МТ –конечное мно-во команд вида

В программе не должно быть каманд с одинаковой левой частью.
9) S-m-n Т.
Существует
всюду определенная вычислимая ф-ия(о.р.ф.)
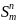 (
( :
: