
- •10) Понятие прямой теоремы и произвольных от неё высказываний
- •11) Т. О проекции:
- •1)Таблица для коньюкции
- •6) Терм
- •10) Т.О полноте
- •1)Дизъюнкция
- •3) Лемма о немонотонной ф-ии
- •6) . Основная т. О рекурсивно перечислимых мн-вах:
- •7) Проблемма остановки
- •8) Оператор примитивной рекурсии
- •9)Изоморфизм моделей
- •2) О существование скнф
- •3) Лемма о немонотонной ф-ии
- •6) Оператор минимизации
- •7) Понятие теории, полные разрешимые , категоричные теории
- •9) Т. Поста (критерий рекурсивности мн-ва).
- •10) . Тезис Чёрча.
- •Штрих шеффера
- •2) Теоремы о нормальных формах
- •8) Машина Тьюринга
- •10) Эрбранова область
- •1. Если в формуле есть константный символ с, то ;
- •2) Формулы ив:
- •3) Класс монотонных функций
- •4) Опр.Класс предполный
- •6)Т. Компактности.
- •10) Теорема о теории модели
- •4) Лемма о нелинейной ф-ии:
- •5) Определение формулы в лп
- •8) Тезис Чёрча.
- •8)Вариант
- •2) . Рекурсивно перечислимымые множества
- •3) Аксиомы ив Генцена.
- •4) . Т. О графике:
- •1) Ч.Р. Фун рек. Пер. Множ.
- •5) Т Поста. О полноте системы булевых ф-ий.
- •6)Т. Компактности.
- •7) Полином Жигалкина
- •8)Ответ
- •9 Вариант
- •3) ) Лемма о немонотонной ф-ии
- •4) Понятие прямой теоремы и произвольных от неё высказываний
- •5)Правило вывода Ив генсена
- •7) Т.(о полноте ив Гильбрта)
- •9) Т. Поста (критерий рекурсивности мн-ва).
- •1)Дизъюнкция
- •2) Фиктивные и существенные переменные.
- •3) Теоремма о разложении булл функции
- •4) Понятие прямой теоремы и произвольных от неё высказываний
- •6)Т о дедукции
- •8)Вывод генсена
- •9) Т. О проекции:
- •3) Теорема о существовании единственной сднф
- •9) Основная т. О рекурсивно перечислимых мн-вах:
- •10) Т. О проекции:
- •2)Кнф и скнф
- •5) Т. О неподвижной точке:
- •Предложение
- •1) Ч.Р. Фун рек. Пер. Множ.
- •Все эквивалентности лв.
- •Если фор-ла , не содержит связную переменную у : ;
- •Если не содержит переменных y,z ; X-свобод
- •9)Наитии Эрбран область
- •10) Два класса префиксов:
- •14Вариант
- •3) Теоремма о разложении булл функции
- •7)Вычисл функции
- •8) Оператор суперпозиции:
- •1) Булевые ф-ции одной переменной
- •2) Принцип двойственности
- •7) Понятие теории, полные разрешимые , категоричные теории
- •8) Оператор примитивной рекурсии
- •9) Т. О неподвижной точке:
- •10) Эрбранова область
- •1. Если в формуле есть константный символ с, то ;
- •2) Т. О замене
- •3) Понятие прямой теоремы и произвольных от неё высказываний
- •5) Не противоречивость множ-ва формул и выводимости
- •6) Два класса префиксов:
- •8) Вычислимость функции на мт
- •5) Т. О дедукции:
- •7) Понятие теории, полные разрешимые , категоричные теории
- •8) Вычислимость функции на мт
- •9) Т. Поста (критерий рекурсивности мн-ва).
- •19 Вариант
- •3) Теоремма о разложении булл функции
- •20 Вариант
- •2) Т. О дедукции.
- •5) Тезис Чёрча.
- •6) Т. О неподвижной точке:
- •7) Оператор суперпозиции:
- •8) Т. Компактности.
1вариант.= 21вариант=41вариант
1)таблица истинности для импликации
x |
y |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
2) лемма о несамодвойственности функции
 .
Тогда
.
Тогда
 (содержат «0» и «1»)
(содержат «0» и «1»)
3) теорема о замене
1.
 —
ф-ла,
—
ф-ла,
 –
ее подформула,
–
ее подформула,
 - ф-лы, причем
- ф-лы, причем
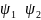 =>
=>
 .
.
2.
 -
ф-лы, причем
-
ф-лы, причем
 ,
x
– символ переменной,
- ф-лы причем
.
Тогда
,
x
– символ переменной,
- ф-лы причем
.
Тогда
 .
.
4) Семантическое дерево
–
это корневое
бинарное дерево, каждое ребро которого
помечено некоторой литерой(симвалы из
х или их отрицаниями), причем ребра
выходящие из одной вершины помечаются
переменной и ее отрицанием, и каждая
ветвь, идущая от корня каждую переменную
содержит не более одного раза.(одновременно
х
или
 не может быть)
не может быть)
5)Определение теории и разрешимость теории
Теория Т-любое мн-во предложений.
Теория
называется полной
, если любые предложения
 ,
либо Т
,
либо Т либо T
либо T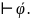
Теория
Т называется разрешимой,
если
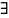 алгоритм, кот за конечное число шагов
получит ответ на вопрос «выводиться
ли
из Т или нет?»
алгоритм, кот за конечное число шагов
получит ответ на вопрос «выводиться
ли
из Т или нет?»
6)элементарная эквивалентность моделей
Опр.
Две формулы наз эквивалентными

Теорема. (об основных эквивалентностях)
Все эквивалентности ЛВ.
Если фор-ла , не содержит связную переменную у :
 ;
;

Если
 не содержит переменных y,z ; x-свобод
не содержит переменных y,z ; x-свобод

 –элементарная
эквивалентность
любое предложение
–элементарная
эквивалентность
любое предложение
 (
истинно на
(
истинно на

истинно на
истинно на
 .
.
7)постоить эрбранову область
строится
так :
 - область:
- область:
1.
Если в формуле есть константный символ
с,
то
 ;
;
2. Если нет константных
символов,=> новый
 ;
;
3.
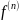 - n-местный
функциональный символ
- n-местный
функциональный символ

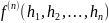
Если не содержит функциональных символов , то Эмбр обл конечно, иначе бесконечна.
Н={c,f(c),f(f(c)),…}
8) Т. о графике:
Опр.пусть
f :
 ,
определим множество
,
определим множество
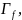
 функции f,
функции f,
Теорема
о графике. Пусть
 тогда
верны утверждения:
тогда
верны утверждения:
1)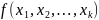 ч.р. фун
ч.р. фун
 рек.
Пер. множ.
рек.
Пер. множ.
2)Если функция всюду определена => f о.р ф. рекурсив. Множ.
9) Оператор суперпозиции:
Суперпозиция
функций f ) и (
) и (
 -это
функция
-это
функция

F=
S(
Другой вариант:

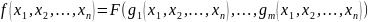
10) Понятие прямой теоремы и произвольных от неё высказываний
Прямая
теорема – высказывание вида A .
Производное высказывание от прямой
теоремы
.
Производное высказывание от прямой
теоремы

Опр. А наз антецедей , В называется консеквент, а само утверждение наз.прямой теоремой; условие В необходимо для А , условие А достаточнодля В.
Расм.также
B .
.
Опр.
B -обратное
,
-обратное
, -против
высказывание,
-против
высказывание,
 теорема обратная противоположной
теорема обратная противоположной
11) Т. О проекции:
Опр.Если рассматривается некоторое мн-во А, то проекцией этого множества А по j-ой координате называется
 ={
={ ,…,
,…, |
| },
если N⊇A,
то его проекция
},
если N⊇A,
то его проекция

Теорема о проекции:
1.Мн-во А рек. Пер. А –проекция рек мн.
2.Если А р.п => всякая проекция р.п. множество.
2.вариант=42вариант=(22наверно)
1)Таблица для коньюкции
x |
y |
xɅy |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
2) Кол-во булевых ф-ций.
Т. Число n-местных
булевых ф-ций равно
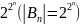
3) Теоремма о разложении булл функции
каждую
n-местную
булеву функцию
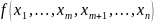 можно представить в форме
можно представить в форме
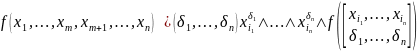 ,
где дизъюнкция берётся по всевозможным
наборам значений переменных
,
где дизъюнкция берётся по всевозможным
наборам значений переменных
 .
.
4) Аксиомы ИВ:
A1)
 ,
,
A2)
 ,
,
A3) ( .
.
Правило
вывода ИВ:
 .(MP-modus
ponens
правило отделения)
.(MP-modus
ponens
правило отделения)
5) Вычислимость функции на МТ
Пусть
функция f:
Опр.
функция
f вычислима на Маш. Тью. М ó
для
любого набора
 машина М : W
машина М : W втом, и только том, случае , когда f(
втом, и только том, случае , когда f(
Теорема.
Всякая МТ
 вычисляет некоторую n-местную
функцию.
вычисляет некоторую n-местную
функцию.
Теорема . существ функции не вычислимые на МТ .Функции вычислимые на МТ называется вычислимыми.
6) Терм
1)Свободные переменные
2)Константные символы
3) Если
 функцианал
символ
функцианал
символ
 –терм ,то f(
–терм ,то f( -
терм.
-
терм.
7) Т. о дедукции:

8) Т. о графике:
Опр. Пусть f : , определим множество функции f,
Теорема о графике. Пусть тогда верны утверждения:
1)
: N→N
ч.р. фун
 рек.
Пер.
рек.
Пер.
2)Если функция всюду определена f: N→N(f-o.р.ф.) рекурсив. Множ.
9) Простейшие функции:
Опр. След функц называются элементарными:
S(x)=x+1;
 (x)=0;
(x)=0;
 (проэкция)
(проэкция)
10) Т.О полноте
(о полноте
ИВ Гильбрта) :
Т.( обобщен теорема о полноте)

3 вариант.=23вариант=43вариант
1)Дизъюнкция
x |
y |
x˅y |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
2) Принцип двойственности
Опр.
 - n-местная
булева ф-ия. Двойственной к f
наз. n-местная
булева ф-ия
- n-местная
булева ф-ия. Двойственной к f
наз. n-местная
булева ф-ия
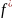 ,
определяемая условием
,
определяемая условием
 для любого набора
для любого набора
 ,где
,где

Следствие.

Опр.
Если – интерпретация функциональных символов,
тогда
– интерпретация функциональных символов,
тогда
 -двойственная
к
-двойственная
к
 .
.
Теорема.
для любых формул и любой интерпретации функций с

3) Лемма о немонотонной ф-ии
 F
F
 M
=>
M
=> [{f,0,1}](замыкание
системы ф-ий из «0» «1» содержит отрицание)
[{f,0,1}](замыкание
системы ф-ий из «0» «1» содержит отрицание)
4)
 - закон
modus ponens
- закон
modus ponens
 - закон
modus tollens;
- закон
modus tollens;
5) Т. компактности.
Мн-во формул Г – не выполнимо
 каждое конечное подмн-во Г выполнимо
каждое конечное подмн-во Г выполнимо
