
- •Дифференциальные уравнения Определения
- •Дифференциальные уравнения первого порядка
- •Уравнения с разделёнными и разделяющимися переменными
- •Однородные уравнения первого порядка
- •Линейные уравнения первого порядка
- •Уравнение в полных дифференциалах
- •Интегрирующий множитель
- •Дифференциальные уравнения высших порядков
- •Уравнения вида
- •Уравнения второго порядка, приводящиеся к уравнениям первого порядка
- •Линейные однородные уравнения. Определения и общие свойства
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения го порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения второго порядка
- •Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения высших порядков
- •Системы обыкновенных дифференциальных уравнений
- •Системы линейных дифференциальных уравнений с постоянными коэффициентами
Системы обыкновенных дифференциальных уравнений
Рассмотрим систему уравнений первого порядка
 ( 1 )
( 1 )
где
 искомые
функции,
искомые
функции,
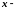 аргумент.
аргумент.
Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.
Решить
систему – значит определить функции
 ,
удовлетворяющие системе уравнений (1)
и данным начальным условиям:
,
удовлетворяющие системе уравнений (1)
и данным начальным условиям:
 ( 2 )
( 2 )
Интегрирование системы (1) производится следующим образом.
Дифференцируем по первое из уравнений (1):
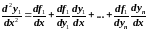
Заменяя
производные
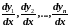 их выражениями
их выражениями
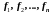 из уравнений (1), будем иметь уравнение
из уравнений (1), будем иметь уравнение
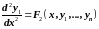 .
.
Дифференцируя полученное уравнение и поступая аналогично предыдущему, получим:
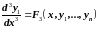 .
.
Продолжая далее, таким же образом получим, наконец, уравнение
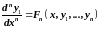 .
.
Итак, получим следующую систему:
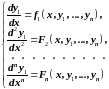 ( 3 )
( 3 )
Из
первых
уравнений определим
 выразив их через
выразив их через
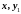 и производные
и производные
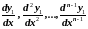 :
:
 ( 4 )
( 4 )
Подставляя
эти выражения в последнее из уравнений
(3), получим уравнение
порядка
для определения
 :
:
 .
( 5 )
.
( 5 )
Решая уравнение (5), определим :
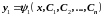 ( 6 )
( 6 )
Дифференцируя выражение (6) раз, найдём производные
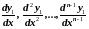
как
функции от
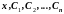 .
Подставляя эти функции в (4), получим
:
.
Подставляя эти функции в (4), получим
:
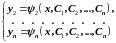 ( 7 )
( 7 )
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Пусть дана система дифференциальных уравнений
 ( 1 )
( 1 )
где
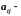 постоянные,
постоянные,
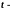 аргумент,
аргумент,
 искомые
функции,
искомые
функции,
 .
Система (1) называется системой
линейных однородных дифференциальных
уравнений с постоянными коэффициентами.
.
Система (1) называется системой
линейных однородных дифференциальных
уравнений с постоянными коэффициентами.
Эту
систему можно решать путём сведения к
одному уравнению
 го
порядка, которое в данном случае будет
линейным. Но можно решать систему (1) и
другим методом, не сводя к уравнению
го
порядка. Этот метод даёт возможность
более наглядно анализировать характер
решений.
го
порядка, которое в данном случае будет
линейным. Но можно решать систему (1) и
другим методом, не сводя к уравнению
го
порядка. Этот метод даёт возможность
более наглядно анализировать характер
решений.
Будем искать решение системы в виде:
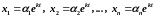 ( 2 )
( 2 )
Надо
определить постоянные
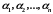 и
так,
чтобы функции
и
так,
чтобы функции
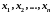 удовлетворяли системе уравнений (1),
т.е.
удовлетворяли системе уравнений (1),
т.е.

Сократив
на
 ,
перенеся все члены в одну сторону и
собрав коэффициенты при
,
получим систему уравнений
,
перенеся все члены в одну сторону и
собрав коэффициенты при
,
получим систему уравнений
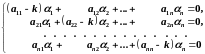 ( 3 )
( 3 )
Выберем и такими, чтобы удовлетворялась система (3). Эта система есть система линейных однородных алгебраических уравнений относительно . Из курса линейной алгебры следует, что она будет иметь нетривиальное решение, если
 ( 4 )
( 4 )
Это уравнение называется характеристическим уравнением для системы (1), его корни называются корнями характеристического уравнения.
В
качестве примера рассмотрим случай,
когда корни характеристического
уравнения
 - действительные и различные.
- действительные и различные.
Для
каждого корня
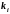 напишем систему уравнений (3) и определим
коэффициенты
напишем систему уравнений (3) и определим
коэффициенты
 .
.
Можно показать, что один из них произвольный, его можно считать равным единице. Таким образом, получаем:
для корня решение системы (1)

для корня решение системы (1)
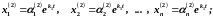
для
корня
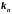 решение системы (1)
решение системы (1)
 .
.
Путём непосредственной подстановки в уравнения можно убедиться, что система функций
 ( 5 )
( 5 )
где
 произвольные
постоянные, тоже является решением
системы дифференциальных уравнений
(1). Это есть общее решение системы (1)
произвольные
постоянные, тоже является решением
системы дифференциальных уравнений
(1). Это есть общее решение системы (1)
