Дифференциальные уравнения Определения

Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную , искомую функцию и её производные и записывается

Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным. Если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

Определение 2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Например:

1. - обыкновенное дифференциальное уравнение 2-го порядка;

2. - уравнение в частных производных 1-го порядка.

Определение 3. Решением дифференциального уравнения называется всякая функция , которая, будучи подставлена в уравнение, превращает его в тождество.

Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка имеет вид . Если это уравнение можно разрешить относительно , то его можно записать в виде . Для такого уравнения справедлива теорема о существовании и единственности решения дифференциального уравнения:

Т е о р е м а. Если в уравнении функция и её частная производная по непрерывны в некоторой области на плоскости , содержащей некоторую точку 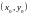, то существует единственное решение этого уравнения удовлетворяющее условию: при

Условие, что при , называется начальным условием и записывается или .

Общим решением дифференциального уравнения первого порядка называется функция которая зависит от одного произвольного постоянного и удовлетворяет условиям:

- она удовлетворяет дифференциальному уравнению при любом конкретном значении постоянного ;

- каково бы ни было начальное условие , можно найти такое значение , что функция удовлетворяет данному начальному условию.

Частным решением называется любая функция , которая получается из общего решения если в последнем произвольному постоянному придать определённое значение .

Уравнения с разделёнными и разделяющимися переменными

Рассмотрим дифференциальное уравнение вида

где правая часть есть произведение функции, зависящей только от , на функцию, зависящую только от , преобразуем его следующим образом

Последнее равенство можно рассматривать как равенство двух дифференциалов, а неопределённые интегралы от них будут отличаться постоянным слагаемым. Интегрируя, получим

Дифференциальное уравнение типа

называют уравнением с разделёнными переменными. Общий интеграл его равен

.

Уравнение вида

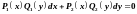
называется уравнением с разделяющимися переменными. Оно может быть приведено к уравнению с разделёнными переменными путём деления обеих его частей на выражение :

,

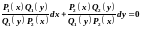или

Однородные уравнения первого порядка

Прежде чем перейти к рассмотрению вопроса о решении однородных уравнений первого порядка познакомимся с понятием однородных функции.

Определение 1. Функция называется однородной функцией -го измерения относительно переменных и , если при любом справедливо тождество

.

Так, например, функция однородная функция первого измерения, т.к. ;

функция однородная функция нулевого измерения, т.к. ;

функция не однородная функция, т.к. однородная функция первого измерения, а однородная функция четвёртого измерения.

Определение 2. Уравнение первого порядка называется однородным относительно и , если функция есть однородная функция нулевого измерения относительно и .

Однородные уравнения первого порядка приводятся к уравнениям с разделяющимися переменными с помощью подстановки

Уравнение вида будет однородным тогда и только тогда, когда функции и будут однородными функциями одного и того же измерения.

Например, однородное уравнение;

не однородное уравнение.

Замечание: Уравнения вида при приводятся к однородным подстановкой где точка пересечения прямых и 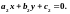Таким образом, для определения и 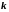необходимо решить систему уравнений:

Если же , то подстановка позволяет разделить переменные.